5.6函数y=Asin(ωχ+φ)课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共27张PPT)
文档属性
| 名称 | 5.6函数y=Asin(ωχ+φ)课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 423.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 16:30:18 | ||
图片预览








文档简介
(共27张PPT)
人教A版(2019)高中数学必修第一册
第五章 三角函数
5.6 函数
课程目标
1. 分别通过对三角函数图像的各种变换的复习和动态演示进一步让学生了解三角函数图像各种变换的实质和内在规律。
2. 通过对函数 (A>0,w>0)图象的探讨,让学生进一步掌握三角函数图像各种变换的内在联系。
数学学科素养
1.逻辑推理: 通过分析 ,研究图像变换注意事项;
2.直观想象:图像的变换.
自主预习,回答问题
阅读课本231-236页,思考并完成以下问题
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
2 、函数y=Asin(ωx+ )的图象与y=sinx的图象有什么关系呢?
1、A,ω, 对y=Asin(ωx+ )图象有什么影响
y=sinx
y=sin(x+ )
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin( x+ )
纵坐标伸长A>1 (缩短0y=Asin( x+ )
y=sinx
y=Asin( x+ )
总结:
向左 >0 (向右 <0)
方法1:按先平移后伸缩的顺序变换
平移| |个单位
纵坐标不变
横坐标不变
知识清单
y=sinx
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin x
纵坐标伸长A>1 (缩短0y=Asin( x+ )
y=sinx
y=Asin( x+ )
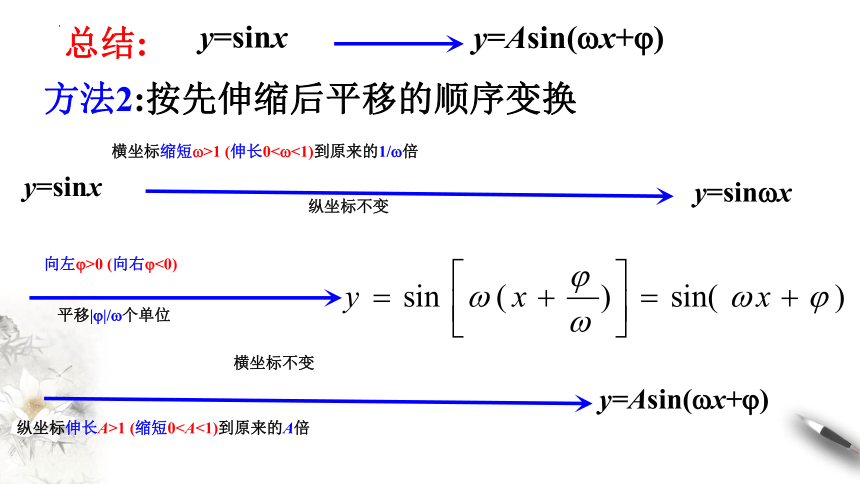
总结:
纵坐标不变
横坐标不变
方法2:按先伸缩后平移的顺序变换
向左 >0 (向右 <0)
平移| |/ 个单位
小试牛刀
1.思考辨析
(1)y=sin 3x的图象向左平移 个单位所得图象的
解析式是y=sin .( )
(2)y=sin x的图象上所有点的横坐标都变为原来
的2倍所得图象的解析式是y=sin 2x.( )
(3)y=sin x的图象上所有点的纵坐标都变为原来
的2倍所得图象的解析式是y= sin x.( )
答案: (1)× (2)× (3)×
3.函数y=A sin(ω x+φ)+1(A>0,ω>0)的最大值为5,则A=________.
4.函数y=3sin( )的频率为________,相位为
________,初相为________.
题型分析 举一反三
题型一
例1、试研究 、
与 的图象关系
1
-1
o
x
y
函数y=sin(x+ )( ≠0)的图象可以看作是把y=sinx的图象上所有的点向左(当 >0时 )或向右(当 <0时 )平行移动 个单位而得到的。
注意:这里平移的对象都是相对于x平移!
解题方法:
2.函数y = sin2x图像向右平移 个单位所得图像的函数表达式为______
题型二
例2.作函数 及 的图象。
1.列表:
x
x
O
y
2
1
2
2
1
3
2. 描点:
y=sinx
y=sin2x
y=sin2x
y=sinx
纵坐标不变
,横坐标
缩短为原来的1/2倍
1. 列表:
x
y
O
2
1
1
3
4
2. 描点:
y=sin x
2
1
y=sinx
0
p
2π
3π
4p
0
2
p
p
2
3
p
2π
x
x
2
1
x
2
1
sin
-1
0
1
0
0
y= sin x
y=sinx
2
1
纵坐标不变,
横坐标
伸长为原来的
2 倍
函数 、 与
的图象间的变化关系。
1
-1
o
x
y
2
-3
函数y=sin x ( >0且 ≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时) 到原来的 倍(纵坐标不变) 而得到的。
解题方法:函数y=sin x( >0)图象
题型三
例3、作函数 及 的简图.
解:
列表
0
0
0
sinx
0
-2
0
2
0
2sinx
0
-1
0
1
0
sinx
2π
π
0
x
描点作图
x
y
0
1
2
-1
-2
π
2π
横坐标不变
纵坐标缩短到原来的一半
y=Sinx y=2Sinx
纵坐标扩大到原来的2倍
横坐标不变
函数 、 与
的图象间的变化关系。
y=sinx
y=2sinx
y= sinx
1
-1
2
-2
o
x
y
3
-3
函数y=Asinx(A>0且A≠1)的图象可以看作是把y=sinx的图象上所有点的纵坐标伸长(当A>1时 )或缩短(当0<A<1时 )到原来的A倍(横坐标不变)而得到的。y=Asinx, x∈R的值域是[-A,A],最大值是A,最小值是-A。
解题方法:函数y=Asinx(A>0)图象
1.如何由 变换得
的图象?
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=3sin(2x+ )
提示:
y=sin(x+ )
y=sinx
函数 y=sinx y=sin(x+ ) 的图象
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3sin(2x+ )的图象
y=sin(2x+ ) 的图象
(1)向左平移
纵坐标不变
(2)横坐标缩短到原来的 倍
人教A版(2019)高中数学必修第一册
第五章 三角函数
5.6 函数
课程目标
1. 分别通过对三角函数图像的各种变换的复习和动态演示进一步让学生了解三角函数图像各种变换的实质和内在规律。
2. 通过对函数 (A>0,w>0)图象的探讨,让学生进一步掌握三角函数图像各种变换的内在联系。
数学学科素养
1.逻辑推理: 通过分析 ,研究图像变换注意事项;
2.直观想象:图像的变换.
自主预习,回答问题
阅读课本231-236页,思考并完成以下问题
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
2 、函数y=Asin(ωx+ )的图象与y=sinx的图象有什么关系呢?
1、A,ω, 对y=Asin(ωx+ )图象有什么影响
y=sinx
y=sin(x+ )
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin( x+ )
纵坐标伸长A>1 (缩短0
y=sinx
y=Asin( x+ )
总结:
向左 >0 (向右 <0)
方法1:按先平移后伸缩的顺序变换
平移| |个单位
纵坐标不变
横坐标不变
知识清单
y=sinx
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin x
纵坐标伸长A>1 (缩短0
y=sinx
y=Asin( x+ )
总结:
纵坐标不变
横坐标不变
方法2:按先伸缩后平移的顺序变换
向左 >0 (向右 <0)
平移| |/ 个单位
小试牛刀
1.思考辨析
(1)y=sin 3x的图象向左平移 个单位所得图象的
解析式是y=sin .( )
(2)y=sin x的图象上所有点的横坐标都变为原来
的2倍所得图象的解析式是y=sin 2x.( )
(3)y=sin x的图象上所有点的纵坐标都变为原来
的2倍所得图象的解析式是y= sin x.( )
答案: (1)× (2)× (3)×
3.函数y=A sin(ω x+φ)+1(A>0,ω>0)的最大值为5,则A=________.
4.函数y=3sin( )的频率为________,相位为
________,初相为________.
题型分析 举一反三
题型一
例1、试研究 、
与 的图象关系
1
-1
o
x
y
函数y=sin(x+ )( ≠0)的图象可以看作是把y=sinx的图象上所有的点向左(当 >0时 )或向右(当 <0时 )平行移动 个单位而得到的。
注意:这里平移的对象都是相对于x平移!
解题方法:
2.函数y = sin2x图像向右平移 个单位所得图像的函数表达式为______
题型二
例2.作函数 及 的图象。
1.列表:
x
x
O
y
2
1
2
2
1
3
2. 描点:
y=sinx
y=sin2x
y=sin2x
y=sinx
纵坐标不变
,横坐标
缩短为原来的1/2倍
1. 列表:
x
y
O
2
1
1
3
4
2. 描点:
y=sin x
2
1
y=sinx
0
p
2π
3π
4p
0
2
p
p
2
3
p
2π
x
x
2
1
x
2
1
sin
-1
0
1
0
0
y= sin x
y=sinx
2
1
纵坐标不变,
横坐标
伸长为原来的
2 倍
函数 、 与
的图象间的变化关系。
1
-1
o
x
y
2
-3
函数y=sin x ( >0且 ≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时) 到原来的 倍(纵坐标不变) 而得到的。
解题方法:函数y=sin x( >0)图象
题型三
例3、作函数 及 的简图.
解:
列表
0
0
0
sinx
0
-2
0
2
0
2sinx
0
-1
0
1
0
sinx
2π
π
0
x
描点作图
x
y
0
1
2
-1
-2
π
2π
横坐标不变
纵坐标缩短到原来的一半
y=Sinx y=2Sinx
纵坐标扩大到原来的2倍
横坐标不变
函数 、 与
的图象间的变化关系。
y=sinx
y=2sinx
y= sinx
1
-1
2
-2
o
x
y
3
-3
函数y=Asinx(A>0且A≠1)的图象可以看作是把y=sinx的图象上所有点的纵坐标伸长(当A>1时 )或缩短(当0<A<1时 )到原来的A倍(横坐标不变)而得到的。y=Asinx, x∈R的值域是[-A,A],最大值是A,最小值是-A。
解题方法:函数y=Asinx(A>0)图象
1.如何由 变换得
的图象?
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=3sin(2x+ )
提示:
y=sin(x+ )
y=sinx
函数 y=sinx y=sin(x+ ) 的图象
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3sin(2x+ )的图象
y=sin(2x+ ) 的图象
(1)向左平移
纵坐标不变
(2)横坐标缩短到原来的 倍
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
