6.10两圆的位置关系[下学期]

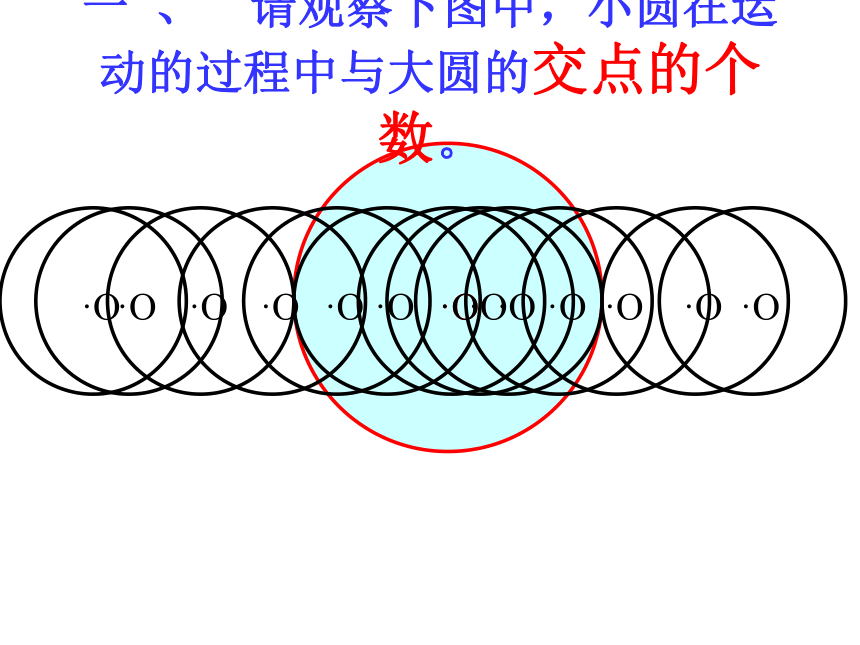
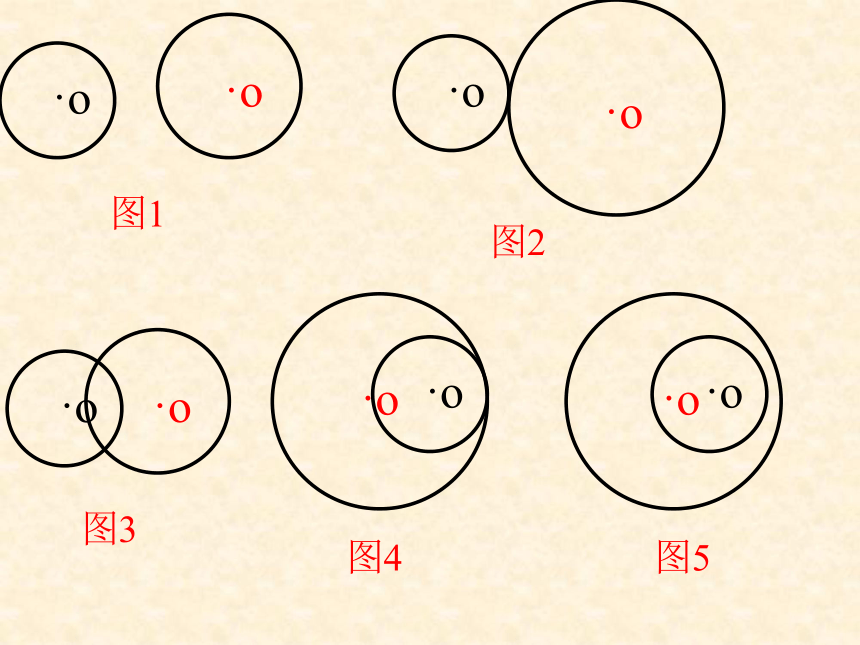
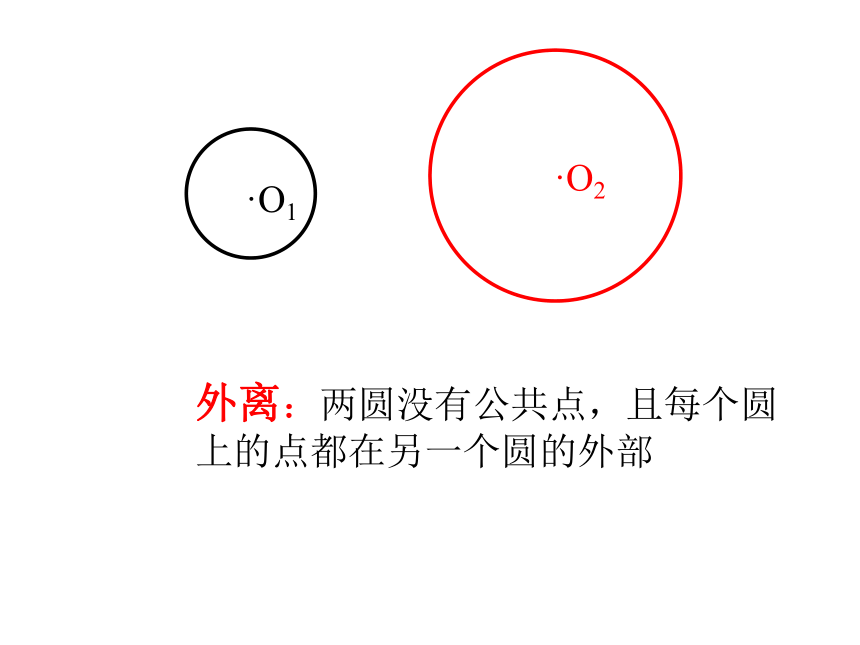
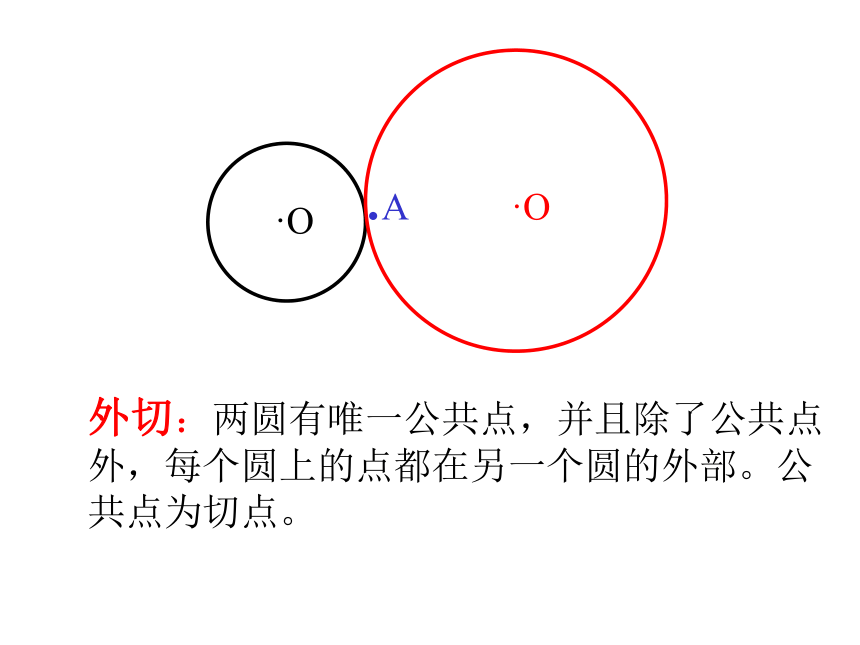
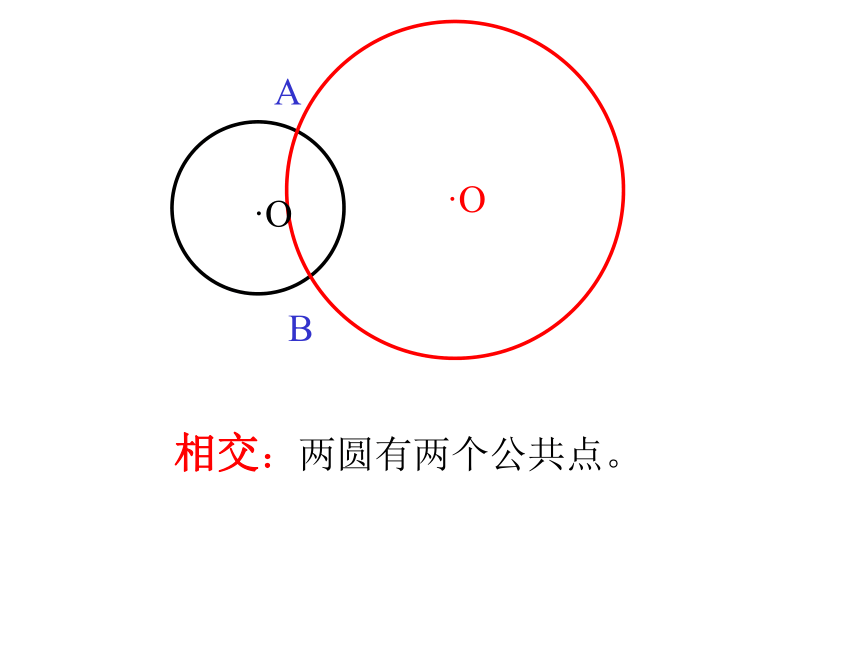
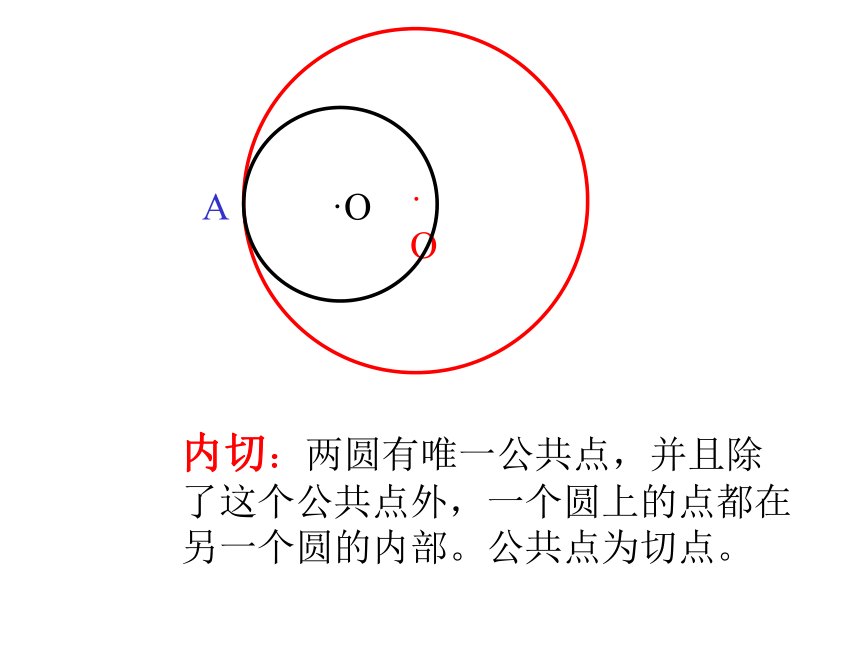
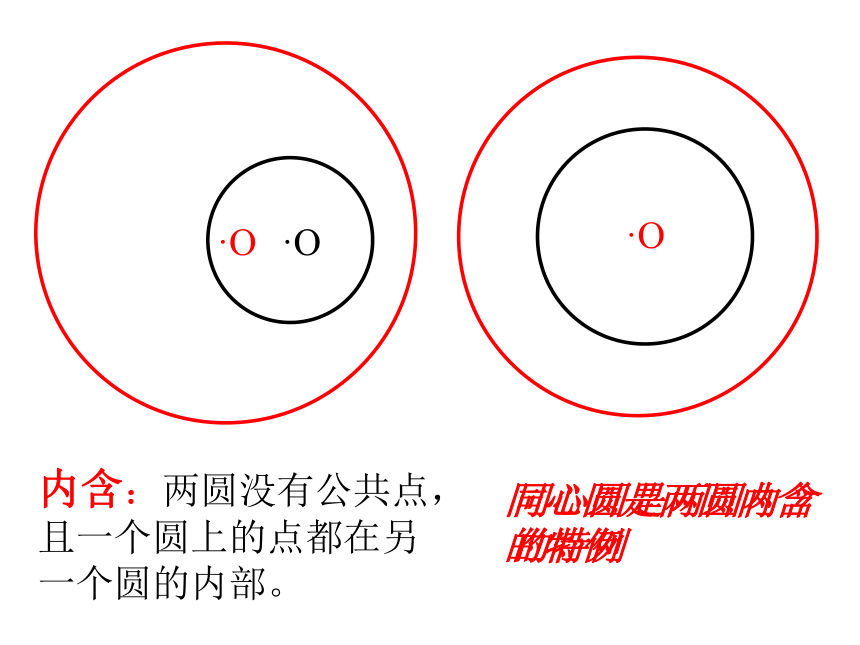
课件25张PPT。圆与圆的位置关系2006.1一 、 请观察下图中，小圆在运动的过程中与大圆的交点的个数。外离：两圆没有公共点，且每个圆上的点都在另一个圆的外部外切：两圆有唯一公共点，并且除了公共点外，每个圆上的点都在另一个圆的外部。公共点为切点。相交：两圆有两个公共点。内切：两圆有唯一公共点，并且除了这个公共点外，一个圆上的点都在另一个圆的内部。公共点为切点。内含：两圆没有公共点，且一个圆上的点都在另一个圆的内部。同心圆是两圆内含的特例同心圆是两圆内含的特例相切相离相交外切内含外离内切二、圆与圆的位置关系没有交点只有一个交点两个交点相切两圆的连心线必经过切点。如果两圆相切，那么其中一个圆的过两圆切点的切线，也是另一个圆的切线。Ｒr切线设两圆的半径为Ｒ和ｒ（R≥r)，圆心距为ｄ，则两圆相切当两圆有唯一公共点时，叫做两圆相切三、两圆各种位置关系的主要性质设两个圆的半径为R和r(R≥r)，圆心距为d，则两圆相交··当两圆有两个公共点时，叫做两圆相交相交两圆的连心线垂直平分两圆的公共弦。O1O2RrAB两圆相离··O1O2Rr设两圆的半径为R的r，圆心距为d，则当两个圆没有公共点时，叫做两圆相离 1.下列说法中不正确的是（ ）
A、两圆有且只有两个公共点，这两圆 相交
B、两圆有唯一公共点，这两圆相切
C、两圆没有公共点，这两圆外离
D、两圆有三个公共点，这两圆重合C四、应用2、 ⊙O1 , ⊙O2半径分别是R=3，r=4。由下面条件判断⊙O1,⊙O2的位置关系：
⑴O1O2=8 cm ⑵O1O2=7 cm ⑶O1O2=5 cm ⑷ O1O2=1 cm ⑸O1O2=0.5 cm ⑹O1O2=0 cm3、⊙O1, ⊙O2半径R=2cm,r=5cm,在下列各种
情况下分别求出O1O2的取值范围
⑴外离 ⑵ 外切 ⑶相交 ⑷ 内切 ⑸内含4、内切的两圆直径分别8cm和14cm，则圆心距D为——
5、两圆圆心距为6，两圆直径是方程x2-12x+27=0的两根，则两圆位置关系是———6、三角形的三边长分别为 4cm、5cm、6cm ，以各顶点为圆心的三个圆两两外切，求各圆的半径？
7、画三个半径分别为 2cm、2.5cm、5cm的圆，使它们两两外切。 1、如图，⊙O1与⊙O2相交于A，B两点，AC是为⊙O1的直径。D，E分别是CA和CB的延长线与⊙O2的交点。已知AC=12，BE=30，BC=AD，求（1）∠C的度数； （2）∠BDE的正弦值。例题E2、如图，⊙O1与⊙O2外切于点E，直线AB，CD过点E，分别交两圆于A、B、C、D，又AF切⊙O2于点F，若AE=4，CE=6，AF=8，求DE的长。BD ··O1O2CDAEF。。MN1、如图， ⊙O1 , ⊙O2 相交于C，D两点， O2 O1 的延长线和⊙O1交于点A；AC，AD的延长线分别与⊙O2相交于E，F。 O2 M ,O2 N分别是弦CE，DF的弦心距。
求证：（1） O2 M= O2 N （2）CE=DF练习二2、如图， O2是⊙O1上的一点，以O2为圆心，O2 O1为半径作一个圆⊙O1交于C，D。直线O1O2分别交⊙O1 , ⊙O2 于点A与点B。 连结AC，BC。
（1）求证：AC=BC；
（2）设⊙O1的半径为r，求AC的长。··。O1CDAB。O2 E定圆O的半径为4cm，动圆P的半径为1cm
1、设⊙ P与⊙ O相外切，那么点P与点O的距离是多少？点P可以在什么样的线上移动？想一想?定圆O的半径为4cm，动圆P的半径为1cm
1、设⊙ P与⊙ O相外切，那么点P与点O的距离是多少？点P可以在什么样的线上移动？2、设⊙ P与⊙ O相内切，情况怎样？
本节课你有什么收获？1、圆和圆的五种位置关系的概念2、圆和圆的五种位置关系的判定及性质概念3、相切两圆的性质外离圆和圆的五种位置关系O1O2>R+rO1O2=R+rR-r