二次函数中有关三角形面积的求解[下学期]
文档属性
| 名称 | 二次函数中有关三角形面积的求解[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 30.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-02 00:00:00 | ||
图片预览



文档简介
课件12张PPT。二次函数二次函数图象与三角形
面积求解想一想令x=0,得y=c, 所以抛物线与y轴的交点坐标为(0,c)
令y=0,得 ,
当 时,抛物线与x轴的有两个交点
当 时,抛物线与x轴的有一个交点
当 时,抛物线与x轴的没有交点例1.求抛物线 与x轴的交点的横坐标?
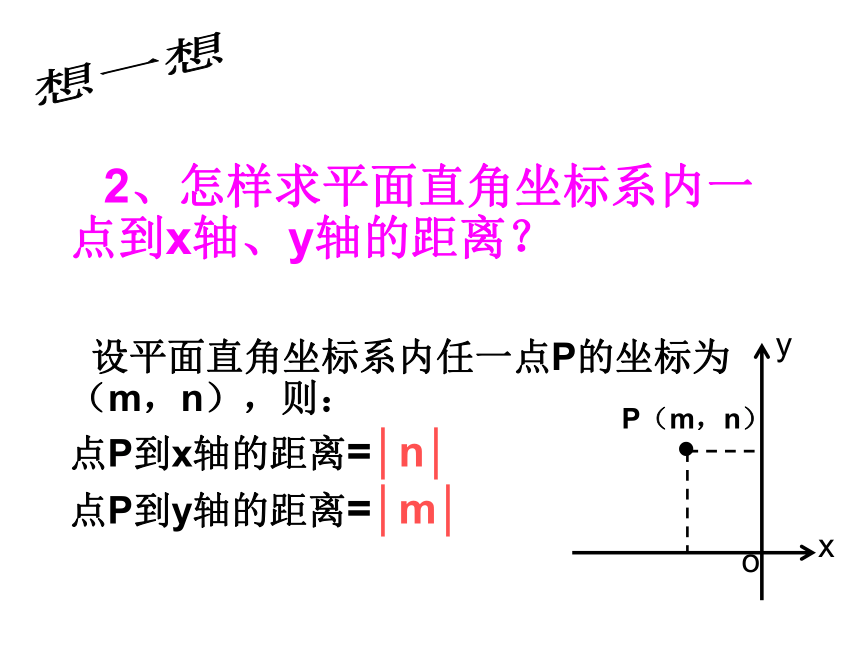
例2抛物线 与x轴有交点吗? 2、怎样求平面直角坐标系内一点到x轴、y轴的距离?
设平面直角坐标系内任一点P的坐标为(m,n),则:
点P到x轴的距离=│n│
点P到y轴的距离=│m│
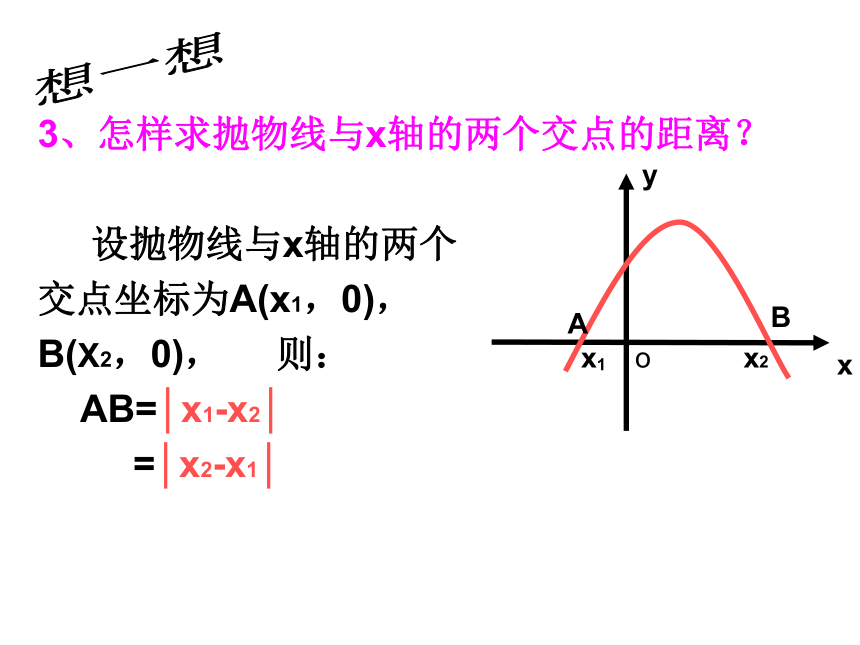
xyoP(m,n)?想一想3、怎样求抛物线与x轴的两个交点的距离?
设抛物线与x轴的两个
交点坐标为A(x1,0),
B(X2,0), 则:
AB=│x1-x2│
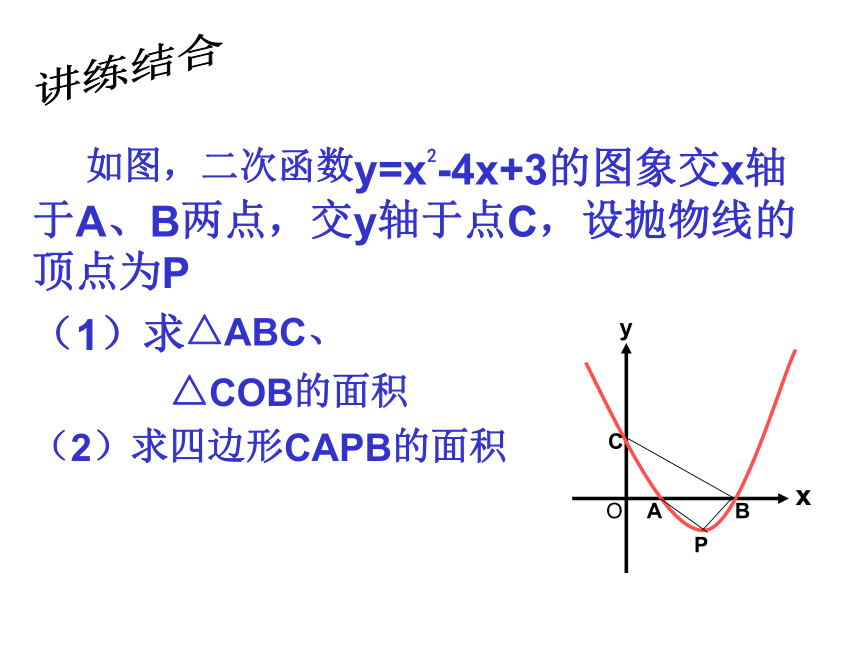
=│x2-x1│xyx1x2ABo想一想 如图,二次函数y=x2-4x+3的图象交x轴于A、B两点,交y轴于点C,设抛物线的顶点为P
(1)求△ABC、
△COB的面积
(2)求四边形CAPB的面积COABxyP讲练结合解:∵ y=x2-4x+3=(x-2)2-1
∴顶点坐标是P(2,-1)
∵ y=x2-4x+3=0时,
x1=1,x2=3
∴A (1,0) , B(3,0)
∵二次函数y=x2-4x+3与y轴的交点是C(0,3)
∴│AB│=│3-1 │= 2 ,│OB│=│3-0 │=3
△ABC的高=│3│=3 ,△ ABP的高=│-1│=1
∴ S△ABC=2×3÷2=3
S△COB=3×3÷2=4.5
∵ S△ABP=2×1÷2=1
∴ S四边形CAPB= S△ABC +S △ABP=3+1=4xyCOABP 如图,二次函数
的图象经过A、B
C三点。
(1)这个二次函数
的解析式。
(2)抛物线上是否
存在一点P(P不与C重合),
使△PAB的面积等于△ABC的面积,
如果存在求出点P的坐标;若不存在,请说明理由?xyo-24-3ABC讲练结合 解:(1)
∵抛物线与x轴交于
A(-2,0), B(4,0)两点
∴设抛物线的解析式为
y=a(x-x1)(x-x2)
=a(x+2)(x-4)
∵抛物线过点C(0,-3)
∴-3=a(0+2)(0-4) 得a=3/8
∴y=3/8(x+2)(x-4)
=3/8x2-3/4x-3xy-204-3ABC(2)存在一点P,使△PAB的面积等于△ABC的面积
设点P的坐标为(x0, y0)
∵ S △ABC =│4-(-2)│×│-3│÷2=9
∴ S △ABP =│4-(-2)│×│y0│÷2=9
∴│y0│=3 即 y0= ±3
当y0=3时,
3/8x2-3/4x-3=3
解得x1=1+ 17, x2=1- 17
当y0= - 3时,
3/8x2-3/4x-3=-3
解得x1=0,x2=2
∴ 符合条件的P有三个,即(1+ 17, 3)
(1- 17, 3) ,(2,-3)xy-240-3ABC课外练习题:
1、如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,于y轴交于C点。点A、C的坐标分别是(-1,0),(0,3/2)。
(1)求此抛物线对应的函数解析式。
(2)若点P是抛物线上位于x轴上方
的一个动点,求△APB面积的最大值。
2、已知函数y=x2+kx-3的图象的顶点
坐标为C,并与x轴相交于两点A、B,且AB=4。
(1)求实数k的值。
(2)若P为抛物线上的一个动点(除点C外),
求使S△ABP=S△ABC成立的点P的坐标。xy0ACB谢谢!再见!
面积求解想一想令x=0,得y=c, 所以抛物线与y轴的交点坐标为(0,c)
令y=0,得 ,
当 时,抛物线与x轴的有两个交点
当 时,抛物线与x轴的有一个交点
当 时,抛物线与x轴的没有交点例1.求抛物线 与x轴的交点的横坐标?
例2抛物线 与x轴有交点吗? 2、怎样求平面直角坐标系内一点到x轴、y轴的距离?
设平面直角坐标系内任一点P的坐标为(m,n),则:
点P到x轴的距离=│n│
点P到y轴的距离=│m│
xyoP(m,n)?想一想3、怎样求抛物线与x轴的两个交点的距离?
设抛物线与x轴的两个
交点坐标为A(x1,0),
B(X2,0), 则:
AB=│x1-x2│
=│x2-x1│xyx1x2ABo想一想 如图,二次函数y=x2-4x+3的图象交x轴于A、B两点,交y轴于点C,设抛物线的顶点为P
(1)求△ABC、
△COB的面积
(2)求四边形CAPB的面积COABxyP讲练结合解:∵ y=x2-4x+3=(x-2)2-1
∴顶点坐标是P(2,-1)
∵ y=x2-4x+3=0时,
x1=1,x2=3
∴A (1,0) , B(3,0)
∵二次函数y=x2-4x+3与y轴的交点是C(0,3)
∴│AB│=│3-1 │= 2 ,│OB│=│3-0 │=3
△ABC的高=│3│=3 ,△ ABP的高=│-1│=1
∴ S△ABC=2×3÷2=3
S△COB=3×3÷2=4.5
∵ S△ABP=2×1÷2=1
∴ S四边形CAPB= S△ABC +S △ABP=3+1=4xyCOABP 如图,二次函数
的图象经过A、B
C三点。
(1)这个二次函数
的解析式。
(2)抛物线上是否
存在一点P(P不与C重合),
使△PAB的面积等于△ABC的面积,
如果存在求出点P的坐标;若不存在,请说明理由?xyo-24-3ABC讲练结合 解:(1)
∵抛物线与x轴交于
A(-2,0), B(4,0)两点
∴设抛物线的解析式为
y=a(x-x1)(x-x2)
=a(x+2)(x-4)
∵抛物线过点C(0,-3)
∴-3=a(0+2)(0-4) 得a=3/8
∴y=3/8(x+2)(x-4)
=3/8x2-3/4x-3xy-204-3ABC(2)存在一点P,使△PAB的面积等于△ABC的面积
设点P的坐标为(x0, y0)
∵ S △ABC =│4-(-2)│×│-3│÷2=9
∴ S △ABP =│4-(-2)│×│y0│÷2=9
∴│y0│=3 即 y0= ±3
当y0=3时,
3/8x2-3/4x-3=3
解得x1=1+ 17, x2=1- 17
当y0= - 3时,
3/8x2-3/4x-3=-3
解得x1=0,x2=2
∴ 符合条件的P有三个,即(1+ 17, 3)
(1- 17, 3) ,(2,-3)xy-240-3ABC课外练习题:
1、如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,于y轴交于C点。点A、C的坐标分别是(-1,0),(0,3/2)。
(1)求此抛物线对应的函数解析式。
(2)若点P是抛物线上位于x轴上方
的一个动点,求△APB面积的最大值。
2、已知函数y=x2+kx-3的图象的顶点
坐标为C,并与x轴相交于两点A、B,且AB=4。
(1)求实数k的值。
(2)若P为抛物线上的一个动点(除点C外),
求使S△ABP=S△ABC成立的点P的坐标。xy0ACB谢谢!再见!
