人教版 八年级下册 第十八章18.1.1 平行四边形的性质(第2课时)ppt(共15张PPT)
文档属性
| 名称 | 人教版 八年级下册 第十八章18.1.1 平行四边形的性质(第2课时)ppt(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 16.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
18.1.1 平行四边形的性质
(第2课时)
第十八章 平行四边形
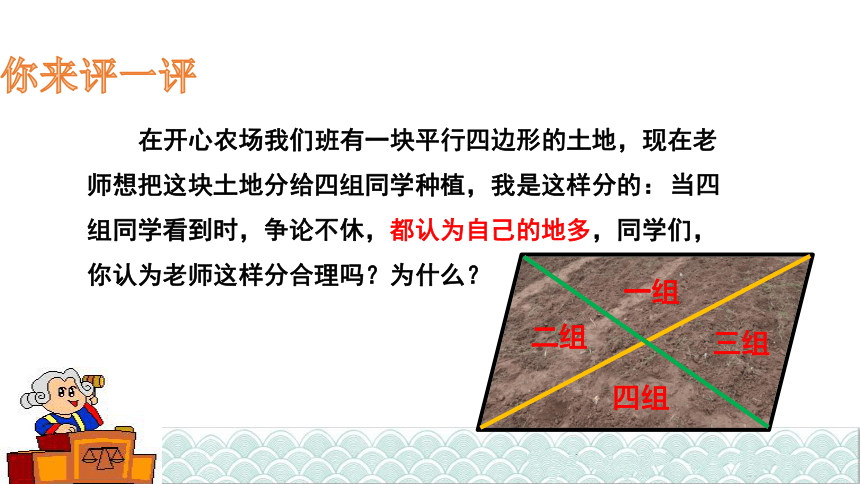
在开心农场我们班有一块平行四边形的土地,现在老师想把这块土地分给四组同学种植,我是这样分的:
一组
二组
三组
四组
你来评一评
当四组同学看到时,争论不休,都认为自己的地多,同学们,你认为老师这样分合理吗?为什么?
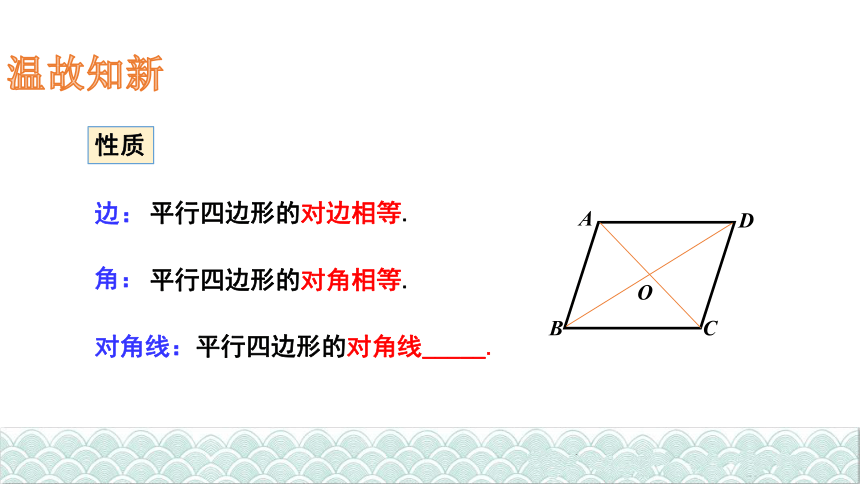
温故知新
性质
边:
角:
平行四边形的对边相等.
平行四边形的对角相等.
对角线:平行四边形的对角线_____.
A
O
D
C
B
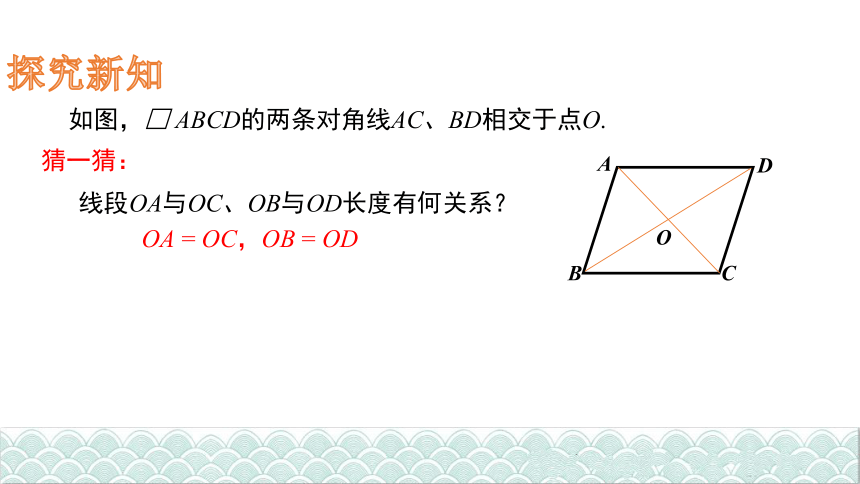
探究新知
如图,□ ABCD的两条对角线AC、BD相交于点O.
猜一猜:
线段OA与OC、OB与OD长度有何关系?
A
O
D
C
B
OA = OC,OB = OD
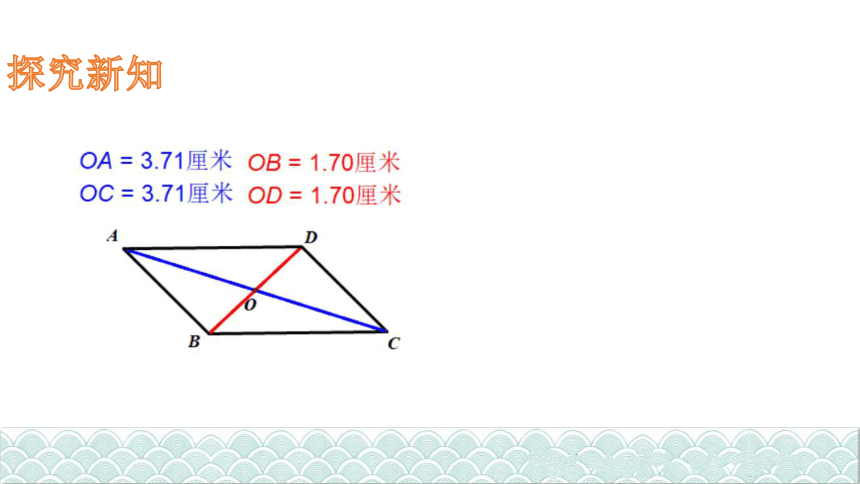
探究新知
O
猜想
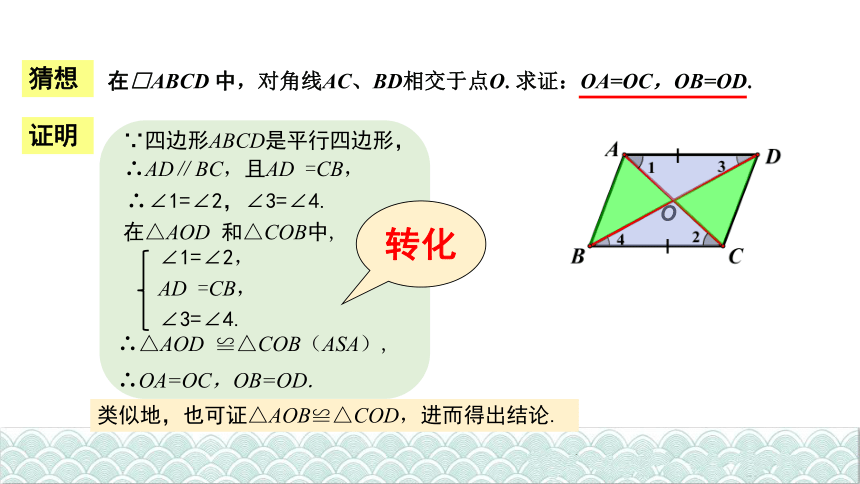
在□ABCD 中,对角线AC、BD相交于点O.求证:OA=OC,OB=OD.
类似地,也可证△AOB≌△COD,进而得出结论.
证明
∵四边形ABCD是平行四边形,
∴AD∥BC,且AD =CB,
∴∠1=∠2,∠3=∠4.
在△AOD 和△COB中,
∴OA=OC,OB=OD.
转化
∠1=∠2,
AD =CB,
∠3=∠4.
∴△AOD ≌△COB(ASA),
O
性质
平行四边形的对角线互相平分.
几何语言:
∵四边形ABCD是平行四边形
∴
学以致用
练习1:如图,在□ ABCD 中,AC=6,BD=16,AO=____; BO=____; CO=____; DO=____;
练习2:如上图,在□ ABCD中,AB=10,
则△COD的周长等于________.
10
10
3
8
AC=6,BD=16,
如图,在□ ABCD 中,AB=10,AD=8,AC⊥BC.
求BC,CD,AC,OA的长,以及□ ABCD的面积.
10
8
10
8
范例讲解
巩固练习
如图,在□ ABCD 中, AD=12,AC=26,∠ADB=900,求OD的长和□ ABCD的面积.
12
26
一组
二组
三组
四组
你能利用平行四边形对角线的性质判定分地合理吗
回顾导入
B
C
A
D
O
S1
S2
S3
S4
△AOD≌△COB
S1 = S3
△AOB≌△COD
S2 = S4
△AOB和△AOD
等底同高
S1 = S2
∴ S1 = S2 = S3= S4
E
平行四边形的两条对角线把平行四边形分成 4 个面积相等的小三角形.
课堂小结
通过本节课的学习,你有什么收获?
知识上:
平行四边形的对角线互相平分.
思想方法上:
转化思想
“猜想—验证—证明”的学习过程
作业布置
必做题:教材第44页第1题和第49页第3题
选做题:如图,在□ ABCD 中, 对角线AC、BD相交于点O,AC=6,BD=8,AB=5.
(1)求□ ABCD的周长;
(2)求□ ABCD的面积.
B
D
A
O
C
一组
二组
三组
四组
你能利用平行四边形对角线的性质判定分地合理吗
回顾导入
B
C
A
D
O
S1
S2
S3
S4
△AOD≌△COB
S1 = S3
△AOB≌△COD
S2 = S4
△AOB和△AOD
等底同高
S1 = S2
∴ S1 = S2 = S3= S4
E
平行四边形的两条对角线把平行四边形分成 4 个面积相等的小三角形.
18.1.1 平行四边形的性质
(第2课时)
第十八章 平行四边形
在开心农场我们班有一块平行四边形的土地,现在老师想把这块土地分给四组同学种植,我是这样分的:
一组
二组
三组
四组
你来评一评
当四组同学看到时,争论不休,都认为自己的地多,同学们,你认为老师这样分合理吗?为什么?
温故知新
性质
边:
角:
平行四边形的对边相等.
平行四边形的对角相等.
对角线:平行四边形的对角线_____.
A
O
D
C
B
探究新知
如图,□ ABCD的两条对角线AC、BD相交于点O.
猜一猜:
线段OA与OC、OB与OD长度有何关系?
A
O
D
C
B
OA = OC,OB = OD
探究新知
O
猜想
在□ABCD 中,对角线AC、BD相交于点O.求证:OA=OC,OB=OD.
类似地,也可证△AOB≌△COD,进而得出结论.
证明
∵四边形ABCD是平行四边形,
∴AD∥BC,且AD =CB,
∴∠1=∠2,∠3=∠4.
在△AOD 和△COB中,
∴OA=OC,OB=OD.
转化
∠1=∠2,
AD =CB,
∠3=∠4.
∴△AOD ≌△COB(ASA),
O
性质
平行四边形的对角线互相平分.
几何语言:
∵四边形ABCD是平行四边形
∴
学以致用
练习1:如图,在□ ABCD 中,AC=6,BD=16,AO=____; BO=____; CO=____; DO=____;
练习2:如上图,在□ ABCD中,AB=10,
则△COD的周长等于________.
10
10
3
8
AC=6,BD=16,
如图,在□ ABCD 中,AB=10,AD=8,AC⊥BC.
求BC,CD,AC,OA的长,以及□ ABCD的面积.
10
8
10
8
范例讲解
巩固练习
如图,在□ ABCD 中, AD=12,AC=26,∠ADB=900,求OD的长和□ ABCD的面积.
12
26
一组
二组
三组
四组
你能利用平行四边形对角线的性质判定分地合理吗
回顾导入
B
C
A
D
O
S1
S2
S3
S4
△AOD≌△COB
S1 = S3
△AOB≌△COD
S2 = S4
△AOB和△AOD
等底同高
S1 = S2
∴ S1 = S2 = S3= S4
E
平行四边形的两条对角线把平行四边形分成 4 个面积相等的小三角形.
课堂小结
通过本节课的学习,你有什么收获?
知识上:
平行四边形的对角线互相平分.
思想方法上:
转化思想
“猜想—验证—证明”的学习过程
作业布置
必做题:教材第44页第1题和第49页第3题
选做题:如图,在□ ABCD 中, 对角线AC、BD相交于点O,AC=6,BD=8,AB=5.
(1)求□ ABCD的周长;
(2)求□ ABCD的面积.
B
D
A
O
C
一组
二组
三组
四组
你能利用平行四边形对角线的性质判定分地合理吗
回顾导入
B
C
A
D
O
S1
S2
S3
S4
△AOD≌△COB
S1 = S3
△AOB≌△COD
S2 = S4
△AOB和△AOD
等底同高
S1 = S2
∴ S1 = S2 = S3= S4
E
平行四边形的两条对角线把平行四边形分成 4 个面积相等的小三角形.
