四川省达州市万源名校2022-2023学年高二下学期入学考试数学(文)试题(解析版)
文档属性
| 名称 | 四川省达州市万源名校2022-2023学年高二下学期入学考试数学(文)试题(解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 21:03:59 | ||
图片预览



文档简介
2022-2023学年四川省达州市万源名校高二下学期入学考试
数学(文)试题
一、单选题
1.在中,“”是“”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也又非必要条件
2.已知,则等于( )
A. B. C. D.
3.在中,,则( )
A. B.
C. D.
4.在等比数列 中,和是方程的两根,则( )
A.3 B.5 C. D.
5.命题:“,”的否定是( )
A., B.,
C., D.,
6.将二进制数化为十进制数,结果为( )
A.11 B.18 C.20 D.21
7.已知直线,若,则( )
A. B. C. D.1
8.某人有1990年北京亚运会吉祥物“盼盼”,2008年北京奥运会吉祥物“贝贝”“晶晶”“欢欢”“迎迎”“妮妮”,2010年广州亚运会吉祥物“阿样”“阿和”“阿如”“阿意”“乐羊羊”,2022年北京冬奥会吉祥物“冰墩墩”,2022年杭州亚运会吉祥物“琮琮”“莲莲”“宸宸”,若他从这15个吉祥物中随机取出两个,这两个吉祥物都是来自在北京举办的运动会的概率是( )
A. B. C. D.
9.执行如图所示的程序框图,输出的的值为( )
A.14 B.20 C.30 D.55
10.已知集合,若“”是“”的充分非必要条件,则的取值范围是( )
A. B. C. D.
11.设点是曲线上任意一点,则点到原点距离的最大值、最小值分别为( )
A.最大值,最小值 B.最大值,最小值1
C.最大值2,最小值 D.最大值2,最小值1
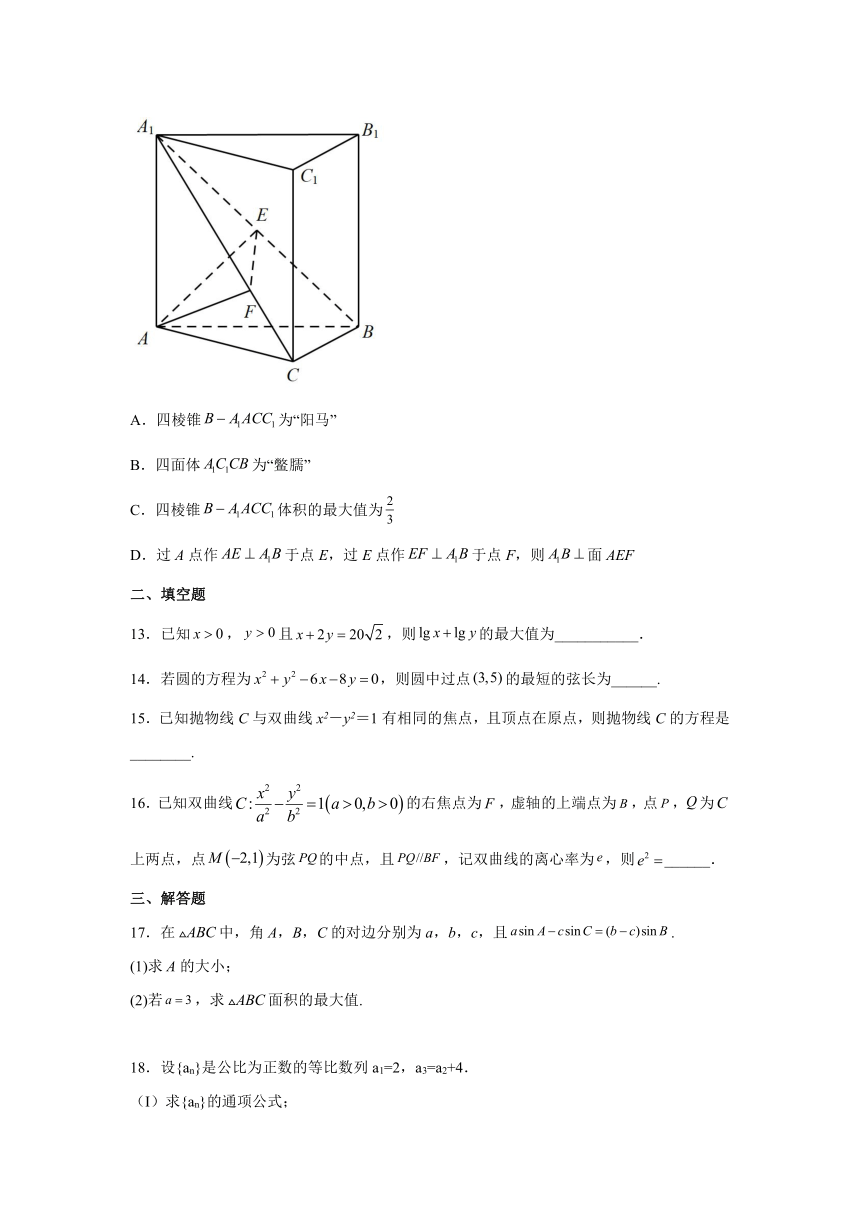
12.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖臑”.如图,在堑堵中,,且.下列说法错误的是( )
A.四棱锥为“阳马”
B.四面体为“鳖臑”
C.四棱锥体积的最大值为
D.过A点作于点E,过E点作于点F,则面AEF
二、填空题
13.已知,且,则的最大值为___________.
14.若圆的方程为,则圆中过点的最短的弦长为______.
15.已知抛物线C与双曲线x2-y2=1有相同的焦点,且顶点在原点,则抛物线C的方程是________.
16.已知双曲线的右焦点为,虚轴的上端点为,点,为上两点,点为弦的中点,且,记双曲线的离心率为,则______.
三、解答题
17.在中,角A,B,C的对边分别为a,b,c,且.
(1)求A的大小;
(2)若,求面积的最大值.
18.设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
19.命题 .
(1)若 为真命题, 求实数 的取值范围;
(2)若 为真命题, 为假命题, 求实数 的取值范围.
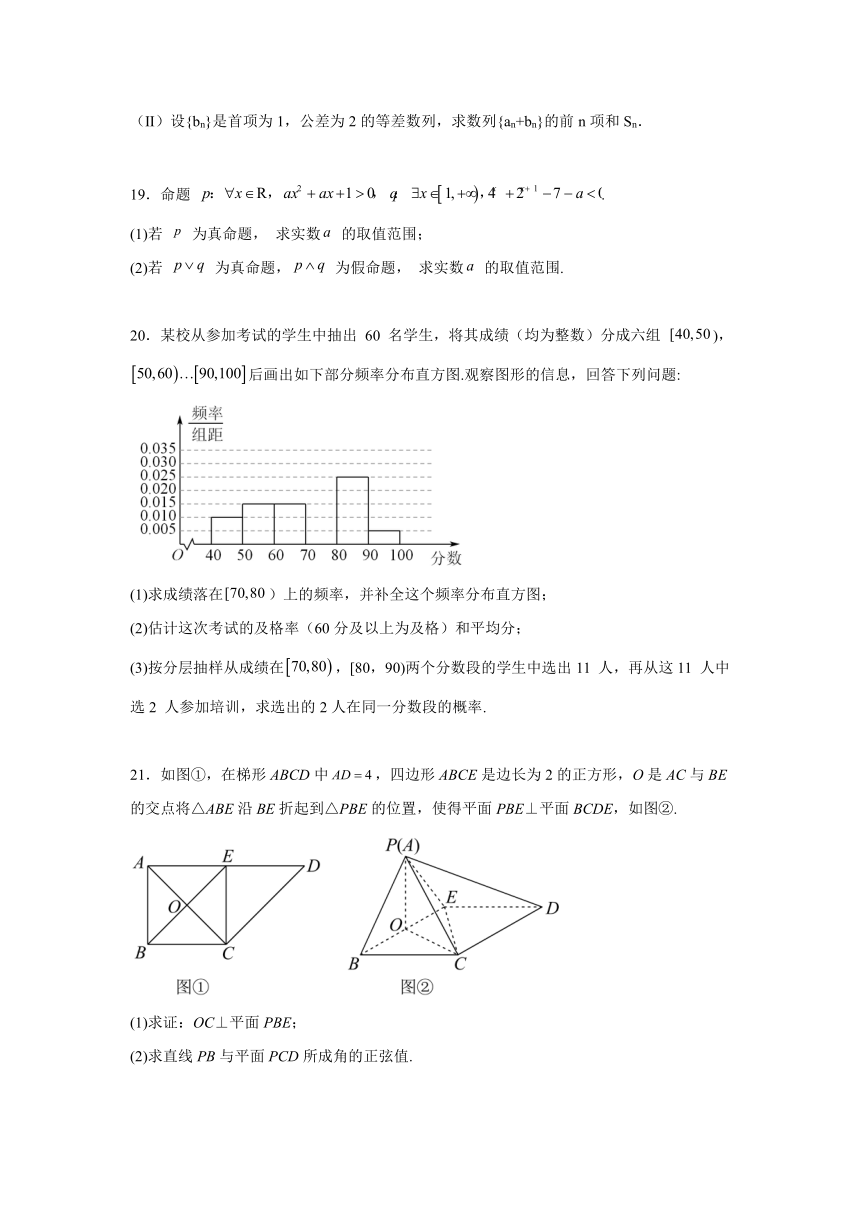
20.某校从参加考试的学生中抽出 60 名学生,将其成绩(均为整数)分成六组 ),后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求成绩落在)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)按分层抽样从成绩在,[80,90)两个分数段的学生中选出11 人,再从这11 人中选2 人参加培训,求选出的2人在同一分数段的概率.
21.如图①,在梯形ABCD中,四边形ABCE是边长为2的正方形,O是AC与BE的交点将△ABE沿BE折起到△PBE的位置,使得平面PBE⊥平面BCDE,如图②.
(1)求证:OC⊥平面PBE;
(2)求直线PB与平面PCD所成角的正弦值.
22.已知双曲线的左、右焦点分别为、,直线过右焦点且与双曲线交于、两点.
(1)若双曲线的离心率为,虚轴长为,求双曲线的焦点坐标;
(2)设,,若的斜率存在,且,求的斜率;
(3)设的斜率为,,求双曲线的方程.
2022-2023学年四川省达州市万源名校高二下学期入学考试
数学(文)试题
一、单选题
1.在中,“”是“”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也又非必要条件
【答案】C
【分析】利用充分条件、必要条件的定义直接判断作答.
【详解】在中,,
所以“”是“”的充要条件.
故选:C
2.已知,则等于( )
A. B. C. D.
【答案】C
【分析】利用三角函数诱导公式即可求得的值.
【详解】
故选:C
3.在中,,则( )
A. B.
C. D.
【答案】B
【分析】根据向量的运算的几何表示结合条件即得.
【详解】∵,
∴,又
∴.
故选:B.
4.在等比数列 中,和是方程的两根,则( )
A.3 B.5 C. D.
【答案】C
【分析】设等比数列的公比为,由韦达定理可得,再根据等比数列的性质即可得解.
【详解】设等比数列的公比为,
因为和是方程的两根,
所以,
所以,
由等比数列的性质得,,
所以,则.
故选:C.
5.命题:“,”的否定是( )
A., B.,
C., D.,
【答案】C
【分析】根据存在量词命题的否定形式,直接判断选项.
【详解】存在量词命题的否定是全称量词命题,所以“,”的否定是“,”.
故选:C
6.将二进制数化为十进制数,结果为( )
A.11 B.18 C.20 D.21
【答案】D
【分析】根据不同进制转化算法计算可得.
【详解】解:.
故选:D
7.已知直线,若,则( )
A. B. C. D.1
【答案】B
【分析】由两直线垂直,斜率的关系列方程直接解得.
【详解】因为所以的斜率为.
因为,所以的斜率必存在,且,所以.
所以,解得:.
故选:B
8.某人有1990年北京亚运会吉祥物“盼盼”,2008年北京奥运会吉祥物“贝贝”“晶晶”“欢欢”“迎迎”“妮妮”,2010年广州亚运会吉祥物“阿样”“阿和”“阿如”“阿意”“乐羊羊”,2022年北京冬奥会吉祥物“冰墩墩”,2022年杭州亚运会吉祥物“琮琮”“莲莲”“宸宸”,若他从这15个吉祥物中随机取出两个,这两个吉祥物都是来自在北京举办的运动会的概率是( )
A. B. C. D.
【答案】B
【分析】先得到15个吉祥物中,来自北京举办的运动会的有7个,再根据组合知识计算出相应的概率.
【详解】15个吉祥物中,来自北京举办的运动会的有7个,
他从这15个吉祥物中随机取出两个,这两个吉祥物都是来自在北京举办的运动会的概率为.
故选:B
9.执行如图所示的程序框图,输出的的值为( )
A.14 B.20 C.30 D.55
【答案】C
【分析】根据程序框图分析即可.
【详解】开始:,
,
不成立,循环,
,
不成立,循环,
,
不成立,循环,
,
成立,终止程序,
输出,
故选:C.
10.已知集合,若“”是“”的充分非必要条件,则的取值范围是( )
A. B. C. D.
【答案】A
【分析】先根据不等式的解法求集合,根据题意可得A是B的真子集,结合真子集关系分析求解.
【详解】由题意可得:,或,
若“”是“”的充分非必要条件,则A是B的真子集,
所以.
故选:A.
11.设点是曲线上任意一点,则点到原点距离的最大值、最小值分别为( )
A.最大值,最小值 B.最大值,最小值1
C.最大值2,最小值 D.最大值2,最小值1
【答案】B
【分析】由题设明确点到原点距离为,结合曲线方程,利用基本不等式可得的最小值和最大值,即可得答案.
【详解】由题意知点到原点距离为 ,
由于点是曲线上任意一点,可得,
当且仅当时取等号,即曲线上的点到原点距离最小,最小值为1;
又因为,所以,
当且仅当时取等号,
故,即,当且仅当时取等号,
即点到原点距离的最大值为,
故选:B
12.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖臑”.如图,在堑堵中,,且.下列说法错误的是( )
A.四棱锥为“阳马”
B.四面体为“鳖臑”
C.四棱锥体积的最大值为
D.过A点作于点E,过E点作于点F,则面AEF
【答案】C
【分析】根据“阳马”和“鳖膈”的定义,可判断A,B的正误;当且仅当时,四棱锥体积有最大值,求值可判断C的正误;根据题意可证平面,进而判断D的正误.
【详解】底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”,
∴在堑堵中,,侧棱平面,
A选项,∴,又,且,则平面,
∴ 四棱锥为“阳马”,故A正确;
B选项,由,即,又且,
∴平面,∴,则为直角三角形,
又由平面,得为直角三角形,由“堑堵”的定义可得为直角三角形,为直角三角形,∴ 四面体为“鳖膈”,故B正确;
C选项,在底面有,即,当且仅当时取等号,
,最大值为,故C错误;
D选项,因为,,,所以平面,故D正确;
故选:C
二、填空题
13.已知,且,则的最大值为___________.
【答案】2
【分析】利用基本不等式得到,从而得到.
【详解】因为,且,所以,
即,当且仅当时等号成立,
所以.
故答案为:2
14.若圆的方程为,则圆中过点的最短的弦长为______.
【答案】
【分析】由题可知点在圆内,则最短的弦是以为中点的弦,进而即得.
【详解】由题可得圆的标准方程为,即圆是以为圆心,5为半径的圆,
且由,即点在圆内,
则最短的弦是以为中点的弦,
所以圆中过点的最短的弦长为.
故答案为:.
15.已知抛物线C与双曲线x2-y2=1有相同的焦点,且顶点在原点,则抛物线C的方程是________.
【答案】
【分析】设抛物线方程为,求出双曲线的焦点,即抛物线的焦点,从而可得出答案.
【详解】解:由已知可知双曲线的焦点为,
设抛物线方程为,则,
所以,
所以抛物线方程为.
故答案为:
16.已知双曲线的右焦点为,虚轴的上端点为,点,为上两点,点为弦的中点,且,记双曲线的离心率为,则______.
【答案】
【分析】解法一,利用点差法,结合,以及,变形得到,再转化为关于的齐次方程,求解;解法二,设直线,,与双曲线方程联立,利用根与系数的关系表示中点坐标,再转化为关于的齐次方程,求解.
【详解】解法一 由题意知,,则.设,,则两式相减,得.因为的中点为,所以,,又,所以,整理得,所以,得,得.
解法二 由题意知,,则.设直线的方程为,即,代入双曲线方程,得.设,,结合为的中点,得.又,所以,整理得,所以,得,得.
故答案为:
【点睛】思路点睛: 常见的求双曲线离心率的方法:①根据已知条件列方程组,解出,的值,直接利用离心率公式求解即可;②根据已知条件得到一个关于,(或,)的齐次方程,然后转化为关于离心率的方程来求解.
三、解答题
17.在中,角A,B,C的对边分别为a,b,c,且.
(1)求A的大小;
(2)若,求面积的最大值.
【答案】(1)
(2)
【分析】(1)利用正弦定理化角为边,再结合余弦定理,可得,从而得解;
(2)结合(1)中结论,推出,再由得解.
【详解】(1)因为,
由正弦定理角化边得,即
,又
(2)由(1)知,
,得,当且仅当时等号成立,
面积,
面积的最大值为.
18.设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
【答案】(Ⅰ)an=2×2n﹣1=2n(Ⅱ)2n﹣1 2n+1﹣2+n2=2n+1+n2﹣2
【详解】试题分析:(Ⅰ)由{an}是公比为正数的等比数列,设其公比,然后利用a1=2,a3=a2+4可求得q,即可求得{an}的通项公式
(Ⅱ)由{bn}是首项为1,公差为2的等差数列 可求得bn=1+(n﹣1)×2=2n﹣1,然后利用等比数列与等差数列的前n项和公式即可求得数列{an+bn}的前n项和Sn.
解:(Ⅰ)∵设{an}是公比为正数的等比数列
∴设其公比为q,q>0
∵a3=a2+4,a1=2
∴2×q2="2×q+4" 解得q=2或q=﹣1
∵q>0
∴q="2"
∴{an}的通项公式为an=2×2n﹣1=2n
(Ⅱ)∵{bn}是首项为1,公差为2的等差数列
∴bn=1+(n﹣1)×2=2n﹣1
∴数列{an+bn}的前n项和Sn=+=2n+1﹣2+n2=2n+1+n2﹣2
点评:本题考查了等比数列的通项公式及数列的求和,注意题目条件的应用.在用等比数列的前n项和公式时注意辨析q是否为1,只要简单数字运算时不出错,问题可解,是个基础题.
19.命题 .
(1)若 为真命题, 求实数 的取值范围;
(2)若 为真命题, 为假命题, 求实数 的取值范围.
【答案】(1);
(2)或.
【分析】(1)分和两种情况讨论即可;
(2)由题先求出为真时的取值范围,然后分真假或假真两种情况,分别解出即可.
【详解】(1)因为为真命题,
当时,恒成立,符合题意;
当时,,解得,
综上所述,;
(2)若为真,
当时,,,
设,则在上单调递增,
所以,
所以,即,
因为为真命题,且为假命题,
所以真假或假真,
当真假时,有,解得;
当假真时,有,解得;
综上所述,或.
20.某校从参加考试的学生中抽出 60 名学生,将其成绩(均为整数)分成六组 ),后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求成绩落在)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)按分层抽样从成绩在,[80,90)两个分数段的学生中选出11 人,再从这11 人中选2 人参加培训,求选出的2人在同一分数段的概率.
【答案】(1)0.3,补图见详解
(2)0.75;71
(3)
【分析】(1)利用频率和为1计算得到答案,在频率分布直方图中高为频率除以组距,补齐即可.
(2)直接根据频率分布直方图数据计算求解,把每一组的组中值乘以面积相加即可得到平均分.
(3)按分层抽样确定两个分数段人数,列出所有情况,统计满足条件的的种数,计算得到答案.
【详解】(1)由题意,,所以成绩落在)上的频率为0.3,在频率分布直方图中高为0.03,补齐如图
(2)由频率分布直方图中数据知及格率为:,
平均分:.
(3)成绩是70~80分组有人,成绩在80~90分组有人,按分层抽样组抽6人记为,组抽5人记为1,2,3,4,5.
从这11人中抽2人有,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,共55种选法.
两人来自同一组有有,,,,,,,,,,,,,,,,,,,,,,,,共25种选法.
所以两人来自同一组的概率为.
21.如图①,在梯形ABCD中,四边形ABCE是边长为2的正方形,O是AC与BE的交点将△ABE沿BE折起到△PBE的位置,使得平面PBE⊥平面BCDE,如图②.
(1)求证:OC⊥平面PBE;
(2)求直线PB与平面PCD所成角的正弦值.
【答案】(1)证明见解析
(2)
【分析】(1)利用线面垂直得判定定理即可证明;
(2)建立空间直角坐标系,利用空间向量求解线面角得正弦值.
【详解】(1)证明:
∵在图①中四边形为正方形,
∴.
有折叠的特性知,在图②中,,
又平面平面,平面平面,
又平面,
∴平面.
(2)由(1)易知,OB,OC,OP两两垂直.
如图,以O为原点,以OB,OC,OP所在直线分别为x轴,y轴,z轴 建立空间直角坐标系,
则,,,.
∴,,.
设平直PCD的法向量为,
则,即,
令,则,.
∴平面PCD的一个法向量为.
∴.
设直线PB与平面PCD所成角为,
∴.
故直线PB与平面PCD所成角的正弦值为.
22.已知双曲线的左、右焦点分别为、,直线过右焦点且与双曲线交于、两点.
(1)若双曲线的离心率为,虚轴长为,求双曲线的焦点坐标;
(2)设,,若的斜率存在,且,求的斜率;
(3)设的斜率为,,求双曲线的方程.
【答案】(1)
(2)
(3)
【分析】(1)由离心率公式和的关系,即可得到结果;
(2)求出右焦点的坐标,设出直线方程,与双曲线方程联立,由韦达定理结合已知条件,即可求出直线的斜率.
(3)设直线的方程为,与双曲线方程联立,消元,运用韦达定理,结合由题意得出的,两个条件,即可求得双曲线的方程.
【详解】(1)由题意得
解得
故双曲线的焦点坐标为.
(2)双曲线,可得
设,直线的斜率为:
设直线的方程为
联立直线与双曲线的方程,
消去得:
由直线与双曲线有两个交点,则且,即
可得,则
,
,可得:
将代入上式,可得
得,可得
解得,即的斜率为.
(3)右焦点为,设直线的方程为,
联立直线与双曲线的方程,
消去得:
则
由,得
整理得,则
即
则
整理得
因为的斜率,所以,整理得
则,,
所以,
由,得,即
又
则,解得
所以,经检验
所以双曲线的方程为.
数学(文)试题
一、单选题
1.在中,“”是“”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也又非必要条件
2.已知,则等于( )
A. B. C. D.
3.在中,,则( )
A. B.
C. D.
4.在等比数列 中,和是方程的两根,则( )
A.3 B.5 C. D.
5.命题:“,”的否定是( )
A., B.,
C., D.,
6.将二进制数化为十进制数,结果为( )
A.11 B.18 C.20 D.21
7.已知直线,若,则( )
A. B. C. D.1
8.某人有1990年北京亚运会吉祥物“盼盼”,2008年北京奥运会吉祥物“贝贝”“晶晶”“欢欢”“迎迎”“妮妮”,2010年广州亚运会吉祥物“阿样”“阿和”“阿如”“阿意”“乐羊羊”,2022年北京冬奥会吉祥物“冰墩墩”,2022年杭州亚运会吉祥物“琮琮”“莲莲”“宸宸”,若他从这15个吉祥物中随机取出两个,这两个吉祥物都是来自在北京举办的运动会的概率是( )
A. B. C. D.
9.执行如图所示的程序框图,输出的的值为( )
A.14 B.20 C.30 D.55
10.已知集合,若“”是“”的充分非必要条件,则的取值范围是( )
A. B. C. D.
11.设点是曲线上任意一点,则点到原点距离的最大值、最小值分别为( )
A.最大值,最小值 B.最大值,最小值1
C.最大值2,最小值 D.最大值2,最小值1
12.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖臑”.如图,在堑堵中,,且.下列说法错误的是( )
A.四棱锥为“阳马”
B.四面体为“鳖臑”
C.四棱锥体积的最大值为
D.过A点作于点E,过E点作于点F,则面AEF
二、填空题
13.已知,且,则的最大值为___________.
14.若圆的方程为,则圆中过点的最短的弦长为______.
15.已知抛物线C与双曲线x2-y2=1有相同的焦点,且顶点在原点,则抛物线C的方程是________.
16.已知双曲线的右焦点为,虚轴的上端点为,点,为上两点,点为弦的中点,且,记双曲线的离心率为,则______.
三、解答题
17.在中,角A,B,C的对边分别为a,b,c,且.
(1)求A的大小;
(2)若,求面积的最大值.
18.设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
19.命题 .
(1)若 为真命题, 求实数 的取值范围;
(2)若 为真命题, 为假命题, 求实数 的取值范围.
20.某校从参加考试的学生中抽出 60 名学生,将其成绩(均为整数)分成六组 ),后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求成绩落在)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)按分层抽样从成绩在,[80,90)两个分数段的学生中选出11 人,再从这11 人中选2 人参加培训,求选出的2人在同一分数段的概率.
21.如图①,在梯形ABCD中,四边形ABCE是边长为2的正方形,O是AC与BE的交点将△ABE沿BE折起到△PBE的位置,使得平面PBE⊥平面BCDE,如图②.
(1)求证:OC⊥平面PBE;
(2)求直线PB与平面PCD所成角的正弦值.
22.已知双曲线的左、右焦点分别为、,直线过右焦点且与双曲线交于、两点.
(1)若双曲线的离心率为,虚轴长为,求双曲线的焦点坐标;
(2)设,,若的斜率存在,且,求的斜率;
(3)设的斜率为,,求双曲线的方程.
2022-2023学年四川省达州市万源名校高二下学期入学考试
数学(文)试题
一、单选题
1.在中,“”是“”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也又非必要条件
【答案】C
【分析】利用充分条件、必要条件的定义直接判断作答.
【详解】在中,,
所以“”是“”的充要条件.
故选:C
2.已知,则等于( )
A. B. C. D.
【答案】C
【分析】利用三角函数诱导公式即可求得的值.
【详解】
故选:C
3.在中,,则( )
A. B.
C. D.
【答案】B
【分析】根据向量的运算的几何表示结合条件即得.
【详解】∵,
∴,又
∴.
故选:B.
4.在等比数列 中,和是方程的两根,则( )
A.3 B.5 C. D.
【答案】C
【分析】设等比数列的公比为,由韦达定理可得,再根据等比数列的性质即可得解.
【详解】设等比数列的公比为,
因为和是方程的两根,
所以,
所以,
由等比数列的性质得,,
所以,则.
故选:C.
5.命题:“,”的否定是( )
A., B.,
C., D.,
【答案】C
【分析】根据存在量词命题的否定形式,直接判断选项.
【详解】存在量词命题的否定是全称量词命题,所以“,”的否定是“,”.
故选:C
6.将二进制数化为十进制数,结果为( )
A.11 B.18 C.20 D.21
【答案】D
【分析】根据不同进制转化算法计算可得.
【详解】解:.
故选:D
7.已知直线,若,则( )
A. B. C. D.1
【答案】B
【分析】由两直线垂直,斜率的关系列方程直接解得.
【详解】因为所以的斜率为.
因为,所以的斜率必存在,且,所以.
所以,解得:.
故选:B
8.某人有1990年北京亚运会吉祥物“盼盼”,2008年北京奥运会吉祥物“贝贝”“晶晶”“欢欢”“迎迎”“妮妮”,2010年广州亚运会吉祥物“阿样”“阿和”“阿如”“阿意”“乐羊羊”,2022年北京冬奥会吉祥物“冰墩墩”,2022年杭州亚运会吉祥物“琮琮”“莲莲”“宸宸”,若他从这15个吉祥物中随机取出两个,这两个吉祥物都是来自在北京举办的运动会的概率是( )
A. B. C. D.
【答案】B
【分析】先得到15个吉祥物中,来自北京举办的运动会的有7个,再根据组合知识计算出相应的概率.
【详解】15个吉祥物中,来自北京举办的运动会的有7个,
他从这15个吉祥物中随机取出两个,这两个吉祥物都是来自在北京举办的运动会的概率为.
故选:B
9.执行如图所示的程序框图,输出的的值为( )
A.14 B.20 C.30 D.55
【答案】C
【分析】根据程序框图分析即可.
【详解】开始:,
,
不成立,循环,
,
不成立,循环,
,
不成立,循环,
,
成立,终止程序,
输出,
故选:C.
10.已知集合,若“”是“”的充分非必要条件,则的取值范围是( )
A. B. C. D.
【答案】A
【分析】先根据不等式的解法求集合,根据题意可得A是B的真子集,结合真子集关系分析求解.
【详解】由题意可得:,或,
若“”是“”的充分非必要条件,则A是B的真子集,
所以.
故选:A.
11.设点是曲线上任意一点,则点到原点距离的最大值、最小值分别为( )
A.最大值,最小值 B.最大值,最小值1
C.最大值2,最小值 D.最大值2,最小值1
【答案】B
【分析】由题设明确点到原点距离为,结合曲线方程,利用基本不等式可得的最小值和最大值,即可得答案.
【详解】由题意知点到原点距离为 ,
由于点是曲线上任意一点,可得,
当且仅当时取等号,即曲线上的点到原点距离最小,最小值为1;
又因为,所以,
当且仅当时取等号,
故,即,当且仅当时取等号,
即点到原点距离的最大值为,
故选:B
12.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖臑”.如图,在堑堵中,,且.下列说法错误的是( )
A.四棱锥为“阳马”
B.四面体为“鳖臑”
C.四棱锥体积的最大值为
D.过A点作于点E,过E点作于点F,则面AEF
【答案】C
【分析】根据“阳马”和“鳖膈”的定义,可判断A,B的正误;当且仅当时,四棱锥体积有最大值,求值可判断C的正误;根据题意可证平面,进而判断D的正误.
【详解】底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”,
∴在堑堵中,,侧棱平面,
A选项,∴,又,且,则平面,
∴ 四棱锥为“阳马”,故A正确;
B选项,由,即,又且,
∴平面,∴,则为直角三角形,
又由平面,得为直角三角形,由“堑堵”的定义可得为直角三角形,为直角三角形,∴ 四面体为“鳖膈”,故B正确;
C选项,在底面有,即,当且仅当时取等号,
,最大值为,故C错误;
D选项,因为,,,所以平面,故D正确;
故选:C
二、填空题
13.已知,且,则的最大值为___________.
【答案】2
【分析】利用基本不等式得到,从而得到.
【详解】因为,且,所以,
即,当且仅当时等号成立,
所以.
故答案为:2
14.若圆的方程为,则圆中过点的最短的弦长为______.
【答案】
【分析】由题可知点在圆内,则最短的弦是以为中点的弦,进而即得.
【详解】由题可得圆的标准方程为,即圆是以为圆心,5为半径的圆,
且由,即点在圆内,
则最短的弦是以为中点的弦,
所以圆中过点的最短的弦长为.
故答案为:.
15.已知抛物线C与双曲线x2-y2=1有相同的焦点,且顶点在原点,则抛物线C的方程是________.
【答案】
【分析】设抛物线方程为,求出双曲线的焦点,即抛物线的焦点,从而可得出答案.
【详解】解:由已知可知双曲线的焦点为,
设抛物线方程为,则,
所以,
所以抛物线方程为.
故答案为:
16.已知双曲线的右焦点为,虚轴的上端点为,点,为上两点,点为弦的中点,且,记双曲线的离心率为,则______.
【答案】
【分析】解法一,利用点差法,结合,以及,变形得到,再转化为关于的齐次方程,求解;解法二,设直线,,与双曲线方程联立,利用根与系数的关系表示中点坐标,再转化为关于的齐次方程,求解.
【详解】解法一 由题意知,,则.设,,则两式相减,得.因为的中点为,所以,,又,所以,整理得,所以,得,得.
解法二 由题意知,,则.设直线的方程为,即,代入双曲线方程,得.设,,结合为的中点,得.又,所以,整理得,所以,得,得.
故答案为:
【点睛】思路点睛: 常见的求双曲线离心率的方法:①根据已知条件列方程组,解出,的值,直接利用离心率公式求解即可;②根据已知条件得到一个关于,(或,)的齐次方程,然后转化为关于离心率的方程来求解.
三、解答题
17.在中,角A,B,C的对边分别为a,b,c,且.
(1)求A的大小;
(2)若,求面积的最大值.
【答案】(1)
(2)
【分析】(1)利用正弦定理化角为边,再结合余弦定理,可得,从而得解;
(2)结合(1)中结论,推出,再由得解.
【详解】(1)因为,
由正弦定理角化边得,即
,又
(2)由(1)知,
,得,当且仅当时等号成立,
面积,
面积的最大值为.
18.设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
【答案】(Ⅰ)an=2×2n﹣1=2n(Ⅱ)2n﹣1 2n+1﹣2+n2=2n+1+n2﹣2
【详解】试题分析:(Ⅰ)由{an}是公比为正数的等比数列,设其公比,然后利用a1=2,a3=a2+4可求得q,即可求得{an}的通项公式
(Ⅱ)由{bn}是首项为1,公差为2的等差数列 可求得bn=1+(n﹣1)×2=2n﹣1,然后利用等比数列与等差数列的前n项和公式即可求得数列{an+bn}的前n项和Sn.
解:(Ⅰ)∵设{an}是公比为正数的等比数列
∴设其公比为q,q>0
∵a3=a2+4,a1=2
∴2×q2="2×q+4" 解得q=2或q=﹣1
∵q>0
∴q="2"
∴{an}的通项公式为an=2×2n﹣1=2n
(Ⅱ)∵{bn}是首项为1,公差为2的等差数列
∴bn=1+(n﹣1)×2=2n﹣1
∴数列{an+bn}的前n项和Sn=+=2n+1﹣2+n2=2n+1+n2﹣2
点评:本题考查了等比数列的通项公式及数列的求和,注意题目条件的应用.在用等比数列的前n项和公式时注意辨析q是否为1,只要简单数字运算时不出错,问题可解,是个基础题.
19.命题 .
(1)若 为真命题, 求实数 的取值范围;
(2)若 为真命题, 为假命题, 求实数 的取值范围.
【答案】(1);
(2)或.
【分析】(1)分和两种情况讨论即可;
(2)由题先求出为真时的取值范围,然后分真假或假真两种情况,分别解出即可.
【详解】(1)因为为真命题,
当时,恒成立,符合题意;
当时,,解得,
综上所述,;
(2)若为真,
当时,,,
设,则在上单调递增,
所以,
所以,即,
因为为真命题,且为假命题,
所以真假或假真,
当真假时,有,解得;
当假真时,有,解得;
综上所述,或.
20.某校从参加考试的学生中抽出 60 名学生,将其成绩(均为整数)分成六组 ),后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求成绩落在)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)按分层抽样从成绩在,[80,90)两个分数段的学生中选出11 人,再从这11 人中选2 人参加培训,求选出的2人在同一分数段的概率.
【答案】(1)0.3,补图见详解
(2)0.75;71
(3)
【分析】(1)利用频率和为1计算得到答案,在频率分布直方图中高为频率除以组距,补齐即可.
(2)直接根据频率分布直方图数据计算求解,把每一组的组中值乘以面积相加即可得到平均分.
(3)按分层抽样确定两个分数段人数,列出所有情况,统计满足条件的的种数,计算得到答案.
【详解】(1)由题意,,所以成绩落在)上的频率为0.3,在频率分布直方图中高为0.03,补齐如图
(2)由频率分布直方图中数据知及格率为:,
平均分:.
(3)成绩是70~80分组有人,成绩在80~90分组有人,按分层抽样组抽6人记为,组抽5人记为1,2,3,4,5.
从这11人中抽2人有,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,共55种选法.
两人来自同一组有有,,,,,,,,,,,,,,,,,,,,,,,,共25种选法.
所以两人来自同一组的概率为.
21.如图①,在梯形ABCD中,四边形ABCE是边长为2的正方形,O是AC与BE的交点将△ABE沿BE折起到△PBE的位置,使得平面PBE⊥平面BCDE,如图②.
(1)求证:OC⊥平面PBE;
(2)求直线PB与平面PCD所成角的正弦值.
【答案】(1)证明见解析
(2)
【分析】(1)利用线面垂直得判定定理即可证明;
(2)建立空间直角坐标系,利用空间向量求解线面角得正弦值.
【详解】(1)证明:
∵在图①中四边形为正方形,
∴.
有折叠的特性知,在图②中,,
又平面平面,平面平面,
又平面,
∴平面.
(2)由(1)易知,OB,OC,OP两两垂直.
如图,以O为原点,以OB,OC,OP所在直线分别为x轴,y轴,z轴 建立空间直角坐标系,
则,,,.
∴,,.
设平直PCD的法向量为,
则,即,
令,则,.
∴平面PCD的一个法向量为.
∴.
设直线PB与平面PCD所成角为,
∴.
故直线PB与平面PCD所成角的正弦值为.
22.已知双曲线的左、右焦点分别为、,直线过右焦点且与双曲线交于、两点.
(1)若双曲线的离心率为,虚轴长为,求双曲线的焦点坐标;
(2)设,,若的斜率存在,且,求的斜率;
(3)设的斜率为,,求双曲线的方程.
【答案】(1)
(2)
(3)
【分析】(1)由离心率公式和的关系,即可得到结果;
(2)求出右焦点的坐标,设出直线方程,与双曲线方程联立,由韦达定理结合已知条件,即可求出直线的斜率.
(3)设直线的方程为,与双曲线方程联立,消元,运用韦达定理,结合由题意得出的,两个条件,即可求得双曲线的方程.
【详解】(1)由题意得
解得
故双曲线的焦点坐标为.
(2)双曲线,可得
设,直线的斜率为:
设直线的方程为
联立直线与双曲线的方程,
消去得:
由直线与双曲线有两个交点,则且,即
可得,则
,
,可得:
将代入上式,可得
得,可得
解得,即的斜率为.
(3)右焦点为,设直线的方程为,
联立直线与双曲线的方程,
消去得:
则
由,得
整理得,则
即
则
整理得
因为的斜率,所以,整理得
则,,
所以,
由,得,即
又
则,解得
所以,经检验
所以双曲线的方程为.
同课章节目录
