2021-2022学年北京市各地八年级下学期数学期末试题选编第二十章数据的分析练习题(含解析)
文档属性
| 名称 | 2021-2022学年北京市各地八年级下学期数学期末试题选编第二十章数据的分析练习题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 706.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 12:27:13 | ||
图片预览


文档简介
第二十章:数据的分析练习题
一、单选题
1.(2022春·北京西城·八年级统考期末)在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
2.(2022春·北京东城·八年级统考期末)一次数学测试,某小组名同学的成绩统计如下(有两个数据被遮盖):
组员 甲 乙 丙 丁 戊 平均成绩 众数
得分
则被遮盖的两个数据依次是( )
A. B. C. D.
3.(2022春·北京朝阳·八年级统考期末)某农民统计了自己养鸡场1000只鸡出售时质量的数据,如下表:
质量/kg 1.0 1.2 1.5 1.8 2.0
频数 108 226 325 245 96
这组数据的众数是( )
A.1.0 B.1.5 C.1.8 D.2.0
4.(2022春·北京丰台·八年级统考期末)一家鞋店在某种运动鞋进货的过程中,商家关注的是卖出的这种运动鞋尺码组成的一组数据的( )
A.平均数 B.中位数 C.众数 D.方差
5.(2022春·北京海淀·八年级统考期末)下表记录了四名同学最近几次一分钟踢毽子选拔赛成绩的平均数与方差.
姓名 甲 乙 丙 丁
平均数 74.25 70 70 65.75
方差 3.07 4.28 2.57 6.78
根据表中数据,要从中选择两名成绩更好且发挥稳定的同学参加正式比赛,应选择( )
A.甲和乙 B.乙和丙 C.甲和丁 D.甲和丙
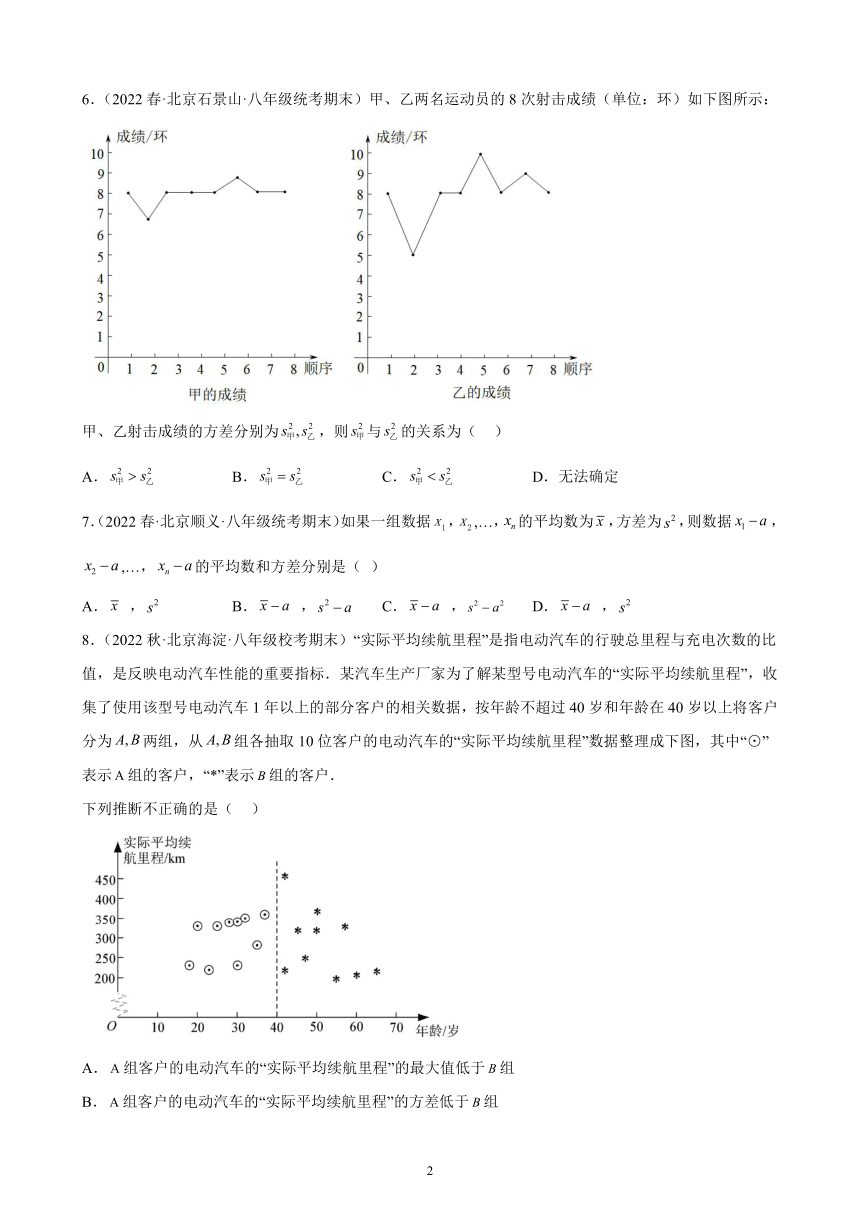
6.(2022春·北京石景山·八年级统考期末)甲、乙两名运动员的8次射击成绩(单位:环)如下图所示:
甲、乙射击成绩的方差分别为,则与的关系为( )
A. B. C. D.无法确定
7.(2022春·北京顺义·八年级统考期末)如果一组数据,,…,的平均数为,方差为,则数据,,…,的平均数和方差分别是( )
A. , B. , C. , D. ,
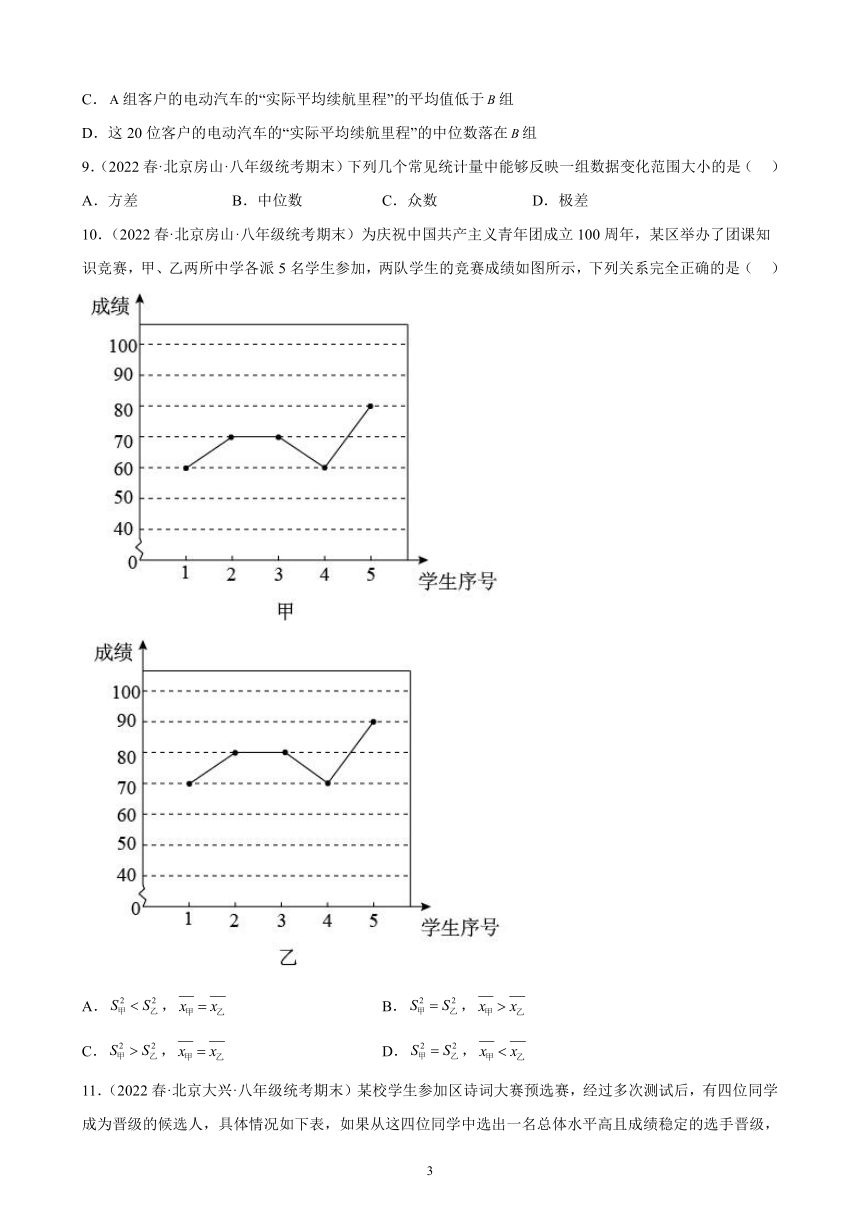
8.(2022秋·北京海淀·八年级校考期末)“实际平均续航里程”是指电动汽车的行驶总里程与充电次数的比值,是反映电动汽车性能的重要指标.某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程”,收集了使用该型号电动汽车1年以上的部分客户的相关数据,按年龄不超过40岁和年龄在40岁以上将客户分为两组,从组各抽取10位客户的电动汽车的“实际平均续航里程”数据整理成下图,其中“⊙”表示组的客户,“*”表示组的客户.
下列推断不正确的是( )
A.组客户的电动汽车的“实际平均续航里程”的最大值低于组
B.组客户的电动汽车的“实际平均续航里程”的方差低于组
C.组客户的电动汽车的“实际平均续航里程”的平均值低于组
D.这20位客户的电动汽车的“实际平均续航里程”的中位数落在组
9.(2022春·北京房山·八年级统考期末)下列几个常见统计量中能够反映一组数据变化范围大小的是( )
A.方差 B.中位数 C.众数 D.极差
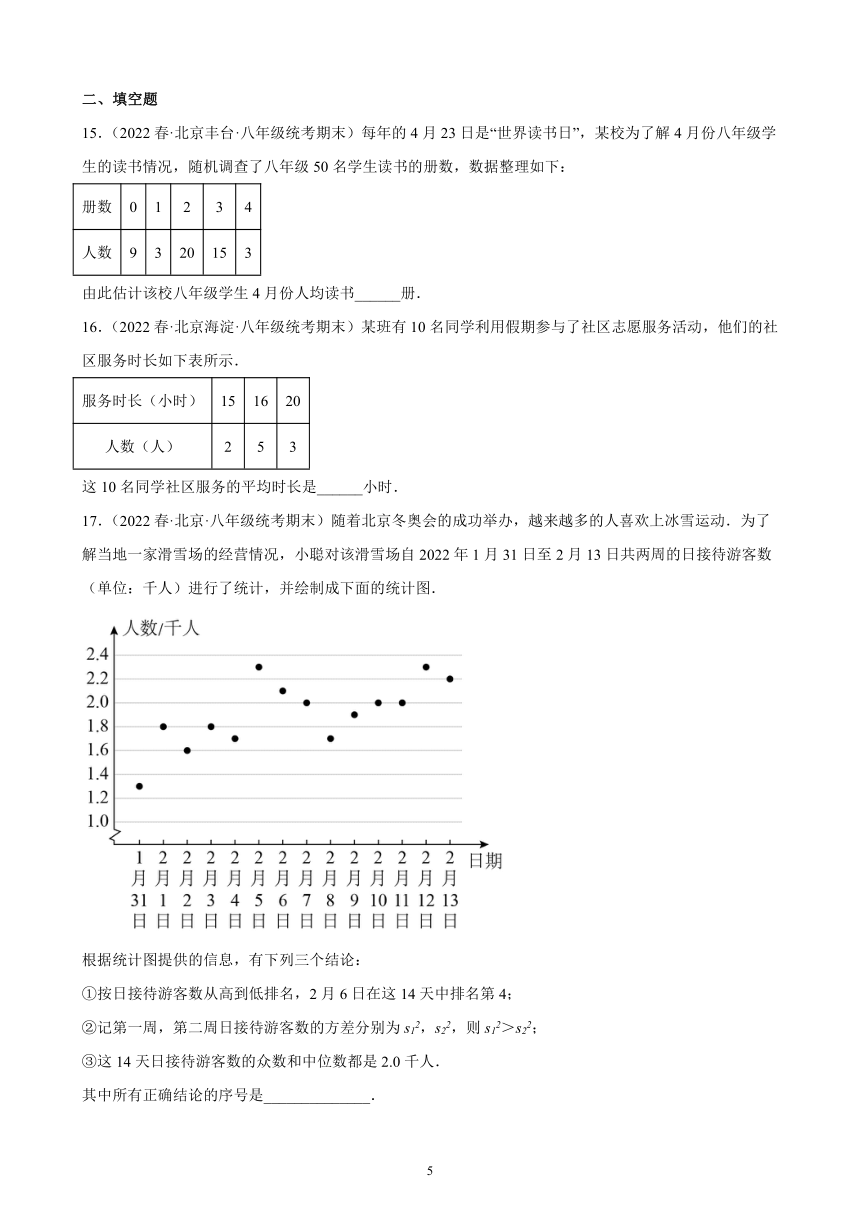
10.(2022春·北京房山·八年级统考期末)为庆祝中国共产主义青年团成立100周年,某区举办了团课知识竞赛,甲、乙两所中学各派5名学生参加,两队学生的竞赛成绩如图所示,下列关系完全正确的是( )
A., B.,
C., D.,
11.(2022春·北京大兴·八年级统考期末)某校学生参加区诗词大赛预选赛,经过多次测试后,有四位同学成为晋级的候选人,具体情况如下表,如果从这四位同学中选出一名总体水平高且成绩稳定的选手晋级,你会推荐( ).
甲 乙 丙 丁
平均分 94 94 92 92
方差 23 35 23 35
A.甲 B.乙 C.丙 D.丁
12.(2022春·北京延庆·八年级统考期末)下表记录了甲、乙、丙、丁四名跳高运动员最近10次训练成绩(单位:cm)的平均数与方差:
甲 乙 丙 丁
平均数 181 183 183 181
方差 1.6 3.4 1.6 3.4
要选择一名成绩好且发挥稳定的同学参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
13.(2022春·北京顺义·八年级统考期末)某校组织环保知识竞赛,为参加区级比赛做选手选拔工作,经过多次测试后,有4名同学成为区级参赛选手的候选人,具体情况如下表:
甲 乙 丙 丁
平均分 90 92 95 95
方差 36 32 21 33
如果从这4名同学中选出1位参加区级比赛(总体水平高且状态稳定),你会推荐( )
A.甲 B.乙 C.丙 D.丁
14.(2022春·北京门头沟·八年级统考期末)下表记录了甲、乙、丙、丁四名滑雪选手次测试成绩的平均数与方差:
甲 乙 丙 丁
平均数(分)
方差
要选择一名成绩较高且状态稳定的选手参加滑雪比赛,那么应该选择的选手是( )
A.甲 B.乙 C.丙 D.丁
二、填空题
15.(2022春·北京丰台·八年级统考期末)每年的4月23日是“世界读书日”,某校为了解4月份八年级学生的读书情况,随机调查了八年级50名学生读书的册数,数据整理如下:
册数 0 1 2 3 4
人数 9 3 20 15 3
由此估计该校八年级学生4月份人均读书______册.
16.(2022春·北京海淀·八年级统考期末)某班有10名同学利用假期参与了社区志愿服务活动,他们的社区服务时长如下表所示.
服务时长(小时) 15 16 20
人数(人) 2 5 3
这10名同学社区服务的平均时长是______小时.
17.(2022春·北京·八年级统考期末)随着北京冬奥会的成功举办,越来越多的人喜欢上冰雪运动.为了解当地一家滑雪场的经营情况,小聪对该滑雪场自2022年1月31日至2月13日共两周的日接待游客数(单位:千人)进行了统计,并绘制成下面的统计图.
根据统计图提供的信息,有下列三个结论:
①按日接待游客数从高到低排名,2月6日在这14天中排名第4;
②记第一周,第二周日接待游客数的方差分别为s12,s22,则s12>s22;
③这14天日接待游客数的众数和中位数都是2.0千人.
其中所有正确结论的序号是______________.
18.(2022春·北京西城·八年级统考期末)射击运动员小东10次射击的成绩(单位:环):7.5,8,7.5,8.5,9,7,7,10,8.5,8.这10次成绩的平均数是8.1,方差是0.79,如果小东再射击一次,成绩为10环,则小东这11次成绩的方差______0.79.(填“大于”、“等于”或“小于”)
19.(2022春·北京东城·八年级统考期末)甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是,,,,则射击成绩最稳定的是______.(填“甲、乙、丙、丁”中的一位)
20.(2022春·北京朝阳·八年级统考期末)某市2021年和2022年5月1日至5日每日最高气温(单位:℃)如下表:
1日 2日 3日 4日 5日
2021年 22 22 24 24 25
2022年 27 26 31 33 30
则这五天的最高气温更稳定的是______年(填“2021”或“2022”).
21.(2022春·北京丰台·八年级统考期末)农科院为某地选择甲、乙两种甜玉米种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题,他们各用10块自然条件相同的试验田进行试验,下图是试验后得到的各试验田两种种子每公顷的产量(单位:t).已知甲、乙两种甜玉米种子的平均产量相差不大,那么由样本估计总体,推测这个地区比较适合种植______(填“甲”或“乙”)种甜玉米,理由是_____________________.
22.(2022春·北京通州·八年级统考期末)寒假期间,滑雪冬令营的同学们都参加了“单板滑雪”这个项目的40次的训练测试,每次测试成绩分别为5分,4分,3分,2分,1分五档,甲、乙两位同学在这个项目的测试成绩统计结果如图所示:
结合图中数据,请你从平均数、众数、中位数、方差中选择一方面评论一下两位同学的滑雪成绩_______.
三、解答题
23.(2022春·北京大兴·八年级统考期末)某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).
根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为________,图①中m的值为_______;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
24.(2022春·北京东城·八年级统考期末)为响应“带动三亿人参与冰雪运动”的号召,某校七、八年级举行了“冰雪运动知识竞赛”.为了解学生对冰雪运动知识的掌握情况,学校从两个年级分别随机抽取了20名学生的竞赛成绩(满分10分,6分及6分以上为合格)进行整理、描述和分析,下面给出了部分信息:
a.七年级20名学生的测试成绩为:
7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,7,9,7,10,6.
b.八年级20名学生的测试成绩条形统计图如图所示:
c.七、八年级抽取的学生的测试成绩的平均数、众数、中位数如下表所示:
年纪 平均数 众数 中位数
七年级 7.5 n 7
八年级 m 8 p
请你根据以上提供的信息,解答下列问题:
(1)上表中m=______,n=______,p=______;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生对冰雪运动知识掌握较好?请说明理由(写出一条理由即可);
(3)该校八年级共400名学生参加了此次测试活动,估计八年级参加此次测试活动成绩合格的学生人数.
25.(2022春·北京朝阳·八年级统考期末)为了解我国2022年25个地区第一季度快递业务收入情况,收集了这25个地区第一季度快递业务收入(单位:亿元)的数据,并对数据进行了整理、描述和分析,给出如下信息.
a.排在前5位的地区第一季度快递业务收入的数据分别为:
534.9 437.0 270.3 187.7 104.0
b.其余20个地区第一季度快递业务收入的数据的频数分布表如下:
快递业务收入x
频数 6 10 1 3
c.第一季度快递业务收入的数据在这一组的是:
20.2 20.4 22.4 24.2 26.1 26.5 28.5 34.4 39.1 39.8
d.排在前5位的地区、其余20个地区、全部25个地区第一季度快递业务收入的数据的平均数、中位数如下:
前5位的地区 其余20个地区 全部25个地区
平均数 306.8 29.9 n
中位数 270.3 m 28.5
根据以上信息,回答下列问题:
(1)表中m的值为______;
(2)在下面3个数中,与表中n的值最接近的是______(填写序号);
①30 ②85 ③150
(3)根据(2)中的数据,预计这25个地区2022年全年快递业务收入约为______亿元.
26.(2022春·北京丰台·八年级统考期末)2021年12月《北京市义务教育体育与健康考核评价方案》正式发布,跳绳成为新增的体育中考选考项目.某校体育组为了解八年级学生跳绳的基本情况,从八年级男、女生中各随机抽取了20名学生1分钟跳绳次数,并对数据进行整理、描述和分析.下面给出了部分信息.
a.学生1分钟跳绳次数频数分布直方图如下(数据分成9组:,,…,):
b.男生1分钟跳绳次数在这一组的是:140,141,142,143,144,145,145,147
c.1分钟跳绳次数的平均数、中位数、优秀率如下表:
组别 平均数 中位数 优秀率
男生 139 m 65%
女生 135 138 n
注:《国家中学生体质健康标准》规定:八年级男生1分钟跳绳次数大于或等于135个,成绩为优秀;八年级女生1分钟跳绳次数大于或等于130个,成绩为优秀.
根据以上信息,回答下列问题:
(1)将女生1分钟跳绳次数频数分布直方图补充完整;
(2)写出表中m,n的值;
(3)此次测试中,某学生的1分钟跳绳次数为140个,这名学生的成绩排名超过同组一半的学生,判断该生属于______(填“男生”或“女生”)组;
(4)如果全年级男生人数为100人,女生人数为120人,请估计该年级跳绳成绩优秀的总人数.
27.(2022春·北京顺义·八年级统考期末)2022年北京冬奥会的举办促进了冰雪旅游,小明为了解寒假期间冰雪旅游的消费情况,从某滑雪场的游客中随机抽取了50人,获得了这些游客当天消费额(单位:元)的数据,并对数据进行整理、描述和分析.下面给出部分信息:
a.滑雪场游客消费额数据的频数分布直方图如下(数据分成6组:0≤x<200,200≤x<400,400≤x<600,600≤x<800,800≤x<1000,1000≤x<1200):
b.滑雪场游客消费额数据在400≤x<600这一组的是:410 430 430 440 440 440 450 450 520 540
c.滑雪场游客消费额数据的平均数为420元.
根据以上信息,解决下列问题:
(1)求滑雪场游客消费额数据在600≤x<800这一组的频率,并补全频数分布直方图;
(2)滑雪场游客消费额数据的中位数是 ;
(3)若滑雪场在寒假期间的一个月内日均游客人数为300人,估计滑雪场这个月(按30天计算)的游客消费总额.
28.(2022春·北京房山·八年级统考期末)居家学习期间,为提高学生的身体素质,某中学开展了以“运动战疫情,跳出我青春”为主题的线上跳绳比赛,同学们通过拍摄视频的方式记录下1分钟内的跳绳个数.该学校共有400名同学参加了本次活动,我们从中随机抽取了40名同学的1分钟跳绳个数作为成绩数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.40名同学1分钟跳绳成绩的频数分布表和频数分布直方图如下:
40名同学1分钟跳绳成绩的频数分布表(表1)
跳绳成绩x(个) 频数 频率
2 0.05
8 0.20
m 0.15
8 0.20
n k
6 0.15
6 0.15
合计 40 1.00
b.40名同学1分钟跳绳成绩在这一组的数据如下表(表2)所示:
跳绳成绩(个) 120 125 128 135
频数 3 2 1 2
根据以上信息,回答下列问题:
(1)表1中m的值为______;k的值为______.
(2)补全该校40名学生1分钟跳绳成绩频数分布直方图.
(3)样本数据的中位数是_______.
(4)学校准备对1分钟跳绳成绩“不少于180个”以上的同学进行表彰,通过分析样本数据,估计400名参与者中可获得表彰的有______名.
29.(2022春·北京平谷·八年级统考期末)为了了解某中学八年级160名男生的身体发育情况,从中随机抽取了20名男生的身高进行测量,并对数据进行了整理、描述和分析,下面给出了部分信息.
a.20名男生身高数据如下(单位:cm):168 161 157 165 173 173 166 176 167 174 176 161 173 171 179 169 169 177 162 155
b.经分组整理后的频数分布表与频数分布直方图如图所示:
分组身高x厘米 频数 频率
155≤ x < 160 2 0.10
160≤ x < 165 3 b
165≤ x < 170 6
170≤ x < 175 0.25
175≤ x < 180 a 0.20
合计 20 1
但在列表和画图时,遗漏了频数分布表中的数据和频数分布直方图中相应的条形图.请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)样本数据中,男生身高的中位数是
(4)估计该校八年级男生身高在170-175cm范围内的人数约为
30.(2022春·北京海淀·八年级统考期末)为比较营养液A和营养液B对某种小西红柿产量的影响,甲、乙两个生物小组各选取了10株长势相近的小西红柿秧苗进行对照实验,甲组使用营养液A,乙组使用营养液B.将每株的产量记录整理,并绘制了如下两个条形图.
解答下列问题:
(1)甲组产量的众数为______,乙组产量的中位数为_______;
(2)经过计算发现两组产量的平均数接近,为了使产量更稳定,则应选择营养液______(填“A”或“B”);
(3)产量30个及以上为秧苗长势良好.现在选用第(2)问推荐的营养液培育100株秧苗,请估计长势良好的大约为______株.
参考答案:
1.B
【分析】由于比赛取前5名参加决赛,共有11名选手参加,根据中位数的意义分析即可.
【详解】11个不同的成绩按从小到大排序后,中位数及中位数之后的共有5个数,
故只要知道自己的成绩和中位数就可以知道是否进入决赛了.
故选B.
【点睛】本题考查了中位数意义.解题的关键是正确的求出这组数据的中位数.
2.A
【分析】根据平均数的计算公式先求出丙的得分,再根据方差公式进行计算即可得出答案.
【详解】根据题意得:
(分),
则丙的得分是分;
众数是,
故选A.
【点睛】考查了众数及平均数的定义,解题的关键是根据平均数求得丙的得分,难度不大.
3.B
【分析】出现次数最多的数据即为该组数据的众数,根据定义解答.
【详解】解:出现次数最多的是1.5,即这组数据的众数是1.5,
故选:B.
【点睛】此题考查了众数的定义,熟记定义是解题的关键.
4.C
【分析】商家关注的是哪种尺码销量最多,利用众数定义即可判断.
【详解】解:商家关注的是卖出的这种运动鞋中哪种尺码销量最多,
因此关注的是卖出的这种运动鞋尺码组成的一组数据的众数.
故选C.
【点睛】本题考查众数的应用,掌握众数的定义是解题的关键.
5.D
【分析】根据平均数和方差的意义判断即可.
【详解】解:由表知,甲、乙、丙成绩的平均数高,其中甲、丙成绩的方差小,
所以甲、丙成绩更好且发挥稳定,
故选:D.
【点睛】本题主要考查方差,解题的关键是掌握平均数及方差的意义.
6.C
【分析】结合图形,乙的成绩波动比较大,则波动大的方差就大.
【详解】解:从图看出:甲选手的成绩波动较小,说明它的成绩较稳定;乙选手的成绩的波动较大,则其方差大,即,
故选:C.
【点睛】此题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7.D
【分析】根据题目中的数据可以求得变化后的数据的平均数和方差,从而可以解答本题.
【详解】解:∵,,
∴变化后的数据的平均数为:,
方差为:,
故选:D.
【点睛】本题考查方差、算术平均数,解答本题的关键是明确题意,会计算一组数据的方差和平均数.
8.C
【分析】方差反应数据的波动程度,平均值容易受到最值影响,中位数需分数据为偶数个和奇数个讨论.
【详解】A.由图观察可知,A组的最大值再350km至400km之间,B组最大值再450km以上,故A正确;
B.由图观察可知,A组数据较为集中,B组数据较为分散,所以A组方差小于B组方差,故B正确;
C.由图观察可知,A组集中在300km和350km之间的有6人,250km至300km之间1人,200km至250km之间3人;而B组在300km至350km之间有3人,200km至250km之间有2人,低于200km的有3人,由此分析可知,A组客户的电动汽车的“实际平均续航里程”的平均值高于组,故C错误;
D.由于本组数据共计20个,采用第10个和第11个的平均数作为中位数,由此观察可知,这两个数在B组,故D正确
故选:C.
【点睛】熟练掌握平均数,中位数,方差的意义及影响要素是解题的关键.
9.D
【分析】根据极差是刻画数据离散程度的一个统计量.它能反映数据的波动范围大小解答;
【详解】解:在数据统计中,能反映一组数据变化范围大小的指标是极差,
故选:D.
【点睛】本题考查的是极差、方差、中位数、众数的概念和意义,掌握极差是刻画数据离散程度的一个统计量.它能反映数据的波动范围是解题的关键.
10.B
【分析】分别求出两所中学5名学生的成绩的平均数和方差,即可求解.
【详解】解:根据题意得:甲所中学5名学生的成绩为60,70,70,60,80,
乙所中学5名学生的成绩为70,80,80,70,90,
∴,,
56,
,
∴,.
故选:D
【点睛】本题主要考查了求平均数和方差,熟练掌握求平均数和方差的公式是解题的关键.
11.A
【分析】根据平均分及方差的比较即可求解.
【详解】解:甲的平均分=乙的平均分>丙和丁的平均分,
且,
因此甲的成绩最稳定,应推荐甲去,
故选:A.
【点睛】本题考查了根据方差判断一组数据的稳定性,熟练掌握方差越小越稳定是解题的关键.
12.C
【分析】平均数相同的情况下,根据方差越小,数据越稳定判断即可.
【详解】解:∵
∴从乙和丙中选一个,
∵,
∴丙的成绩方差最小,
∴应该选择丙.
故选:C.
【点睛】此题主要考查了方差和平均数,关键是掌握方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.平均数反映一组数据的一般水平,平均数较大的成绩相应的较好.
13.C
【分析】此题有两个要求:①成绩较好,②状态稳定.所以应选平均分数高、方差小的选手参赛,从而得出答案.
【详解】从表中可知:丙的方差最小、平均分最高,所以应推荐丙.
故选 C.
【点睛】本题考查平均数和方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
14.B
【分析】根据平均数的概念、方差的性质判断即可.
【详解】解:由表格中平均数可知:成绩好的选手是乙、丙,由表格中乙、丙的方差可知:成绩好且发挥稳定的选手是乙,
应该选择的选手是:乙,
故选:B.
【点睛】本题考查的是平均数、方差,解题的关键是掌握方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
15.2
【分析】先根据表格中的数据得出50名学生读书的总册数,然后除以50即可求出平均数.
【详解】解:估计该校八年级学生4月份人均读书(0×9+1×3+2×20+3×15+4×3)÷50=2(册),
由此估计该校八年级学生4月份人均读书2册.
故答案为:2.
【点睛】本题考查的是加权平均数的计算方法,通过样本去估计总体,总体平均数与样本平均数近似相等.
16.17
【分析】根据加权平均数的公式直接代入数据计算即可.
【详解】解:这10名同学社区服务的平均时长是:
=17(小时).
故答案为:17.
【点睛】本题考查了加权平均数,正确理解加权平均数的概念是解题的关键.
17.①②
【分析】①根据统计图数据判断即可;②根据数据的波动情况判断即可;③根据众数和中位数的定义判断即可.
【详解】解:①按日接待游客数从高到低排名,2月6日在这14天中排名第4,说法正确;
②记第一周,第二周日接待游客数的方差分别为s12,s22,则s12>s22,说法正确;
③这14天日接待游客数的众数为2.0千人,中位数为1.90千人,原说法错误.
所以正确结论的序号是①②.
故答案为:①②.
【点睛】本题考查了折线统计图,涉及中位数,方差,众数等知识.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
18.大于
【分析】计算小东这11次成绩的方差后比较即可.
【详解】解:小东这11次成绩的的平均成绩为(8.1×10+10)÷11=≈8.27,
小东这11次成绩的的方差S2=×[2×(7.5 8.27)2+2×(8 8.27)2+2×(8.5 8.27)2+2×(7 8.27)2+2×(10 8.27)2+(9 8.27)2]≈1.02,
即1.02>0.79,
∴小东这11次成绩的方差大于0.79,
故答案为:大于.
【点睛】本题考查求所给数据的方差:一般地设n个数据,x1,x2,…xn的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
19.丙
【分析】根据方差是用来衡量一组数据波动大小的量,故由甲乙丙丁的方差可直接作出判断.
【详解】解:∵,,,,
∴,
∴射击成绩最稳定的是丙.
故答案为:丙.
【点睛】本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
20.2021
【分析】分别计算出这两年的方差,即可判断.
【详解】解:2021年的平均数=23.4,方差==1.44,
2022年的平均数=,方差==6.64,
∵1.44<6.64,
∴2021年的最高气温更稳定,
故答案为:2021.
【点睛】此题考查了根据方差判断稳定性,正确掌握平均数的计算公式及方差的计算公式是解题的关键.
21. 甲 甲的产量比较稳定
【分析】据从图中数据的波动情况分析.
【详解】解:从图中看到,甲的波动比乙的波动小,故甲的产量比较稳定,
所以这个地区比较适合种植甲种甜玉米,理由是甲的产量比较稳定.
故答案为:甲;甲的产量比较稳定.
【点睛】本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
22.从平均数看甲同学成绩好(或从中位数看两个同学的成绩一样或从方差看乙的成绩稳定).答案不唯一
【分析】可以分别求出甲、乙两个同学的平均数、中位数和方差进行分析即可.
【详解】解:情况一:甲的平均数为:,
乙的平均数为:,
∵,
∴从平均数看甲同学成绩好.
情况二:甲的中位数为3,乙的中位数为3,因此从中位数看两个同学的成绩一样.
情况三:甲的方差为:
,
,
∵,
∴从方差看乙的成绩稳定.
故答案为:从平均数看甲同学成绩好(或从中位数看两个同学的成绩一样或从方差看乙的成绩稳定).答案不唯一
【点睛】本题主要考查了通过平均数、中位数、方差作出决策,解题的关键是求出两位同学的平均数、中位数和方差.
23.(Ⅰ)50,20;(Ⅱ)这组数据的平均数是5.9;众数为6;中位数为6.
【分析】(Ⅰ)利用用水量为5t的家庭个数除以其所占百分比即可求出本次接受调查的家庭个数;利用用水量为6.5t的家庭个数除以本次接受调查的家庭个数即得出其所占百分比,即得出m的值.
(Ⅱ)根据加权平均数的公式,中位数,众数的定义即可求出结果.
【详解】(Ⅰ)本次接受调查的家庭个数=,
由题意可知 ,
解得.
故答案为50,20.
(Ⅱ)观察条形统计图,
∵,
∴这组数据的平均数是5.9.
∵在这组数据中,6出现了16次,出现的次数最多,
∴这组数据的众数为6.
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数都是6,
即有,
∴这组数据的中位数为6.
【点睛】本题考查条形统计图与扇形统计图相关联,加权平均数,中位数以及众数.从条形统计图与扇形统计图中找到必要的数据和信息是解答本题的关键.
24.(1)7.5,7,7.5
(2)八年级,理由见解析
(3)360人
【分析】(1)根据平均数、众数、中位数的计算方法求解即可得出m、n、p的值;
(2)从中位数、众数的角度回答即可;
(3)求出七、八年级的总体合格率,利用总体乘以合格率计算即可即可.
(1)
解:由条形图得:(分),
七年级20名学生的测试成绩排序为:
5、5、6、6、6、7、7、7、7、7、7、8、8、8、9、9、9、9、10、10,
七年级学生成绩出现次数最多的是7分,共出现6次,因此七年级学生成绩的众数为7分,即n=7;
八年级学生成绩是20名学生测试成绩中位数位于,11两个位置数据的平均数,
从小到大排列后处在中间位置的两个数的测试成绩为7分,8分
平均数为(分),
因此八年级学生成绩的中位数是7.5分,即p=7.5;
故答案为:7.5,7,7.5;
(2)
解:根据表格七、八年级抽取的学生的测试成绩的平均数、众数、中位数如表所示:
年级 平均数 众数 中位数
七年级 7.5 7 7
八年级 7.5 8 7.5
∵七年八年学生测试成绩平均数相同,八年级学生测试成绩中位数与众数都比七年级学生测试成绩高
∴八年级学生掌握垃圾分类知识较好;
(3)
解:∵6分及6分以上为合格
七年级与八年级学生测试成绩合格人数分别为:18人,
占七八年各随机抽取20名学生的测试成绩的百分比为:
该校七、八年级共400名学生参加此次测试活动成绩合格的学生有(人),
答:我校七、八年级400名学生中测试成绩合格的大约有360人.
【点睛】本题考查了条形统计图、统计表,中位数、众数、平均数的意义,用样本的百分比含量估计总体中的数量,掌握中位数、平均数、众数、样本的百分比含量的计算方法是正确解答的前提.
25.(1)25.15
(2)②
(3)8528
【分析】(1)根据中位数的定义,计算第10个及第11个数据的平均数可得m;
(2)根据前5位的地区的平均数为306.8,其余20个地区的平均数为29.9,求出全部25个地区的收入,再除以25可得n,比较即可;
(3)用第一季度的总收入乘以4即可.
(1)
解:∵6+10=16,
∴其余20个地区的第一季度快递业务收入数据的第10个及第11个数据均在的范围,
∴第10个数据和第11个数据分别为24.2,26.1,
∴中位数m=,
故答案为:25.15;
(2)
∵前5位的地区的平均数为306.8,其余20个地区的平均数为29.9,
∴全部25个地区的收入=306.8×5+29.9×20=2132(亿元),
∴全部25个地区的n=2132÷25=85.28(亿元),
故选:②
(3)
这25个地区2022年全年快递业务收入约为2132×4=8528(亿元),
故答案为8528.
【点睛】此题考查了统计知识,求中位数,求平均数,根据部分的数量求总体,正确理解题意是解题的关键.
26.(1)见解析
(2),
(3)“女生”
(4)149人
【分析】(1)利用抽取女生的总人数和女生跳绳次数频数分布直方图中的数据,求出成绩在之间的人数即可;
(2)利用中位数的定义求m,利用八年级女生1分钟跳绳次数大于或等于130个的人数除以女生总人数求n;
(3)将这名学生的成绩与男生、女生成绩的中位数比较即可;
(4)利用样本估计总体的方法解决.
(1)
解:女生成绩在之间的人数为:,
补全后的频数分布直方图如下图所示:
(2)
解:由男生1分钟跳绳次数频数分布直方图和这一组的数据可知,20名男生中,成绩从低到高排序,第10位和第11位的成绩分别是141,142,
因此男生组的中位数:;
女生1分钟跳绳次数大于或等于130个的人数为:,
因此女生组的优秀率:,
故,;
(3)
解:这名学生的成绩140小于男生组的中位数141.5,大于女生组的中位数138,
因此该生属于“女生”,
故答案为:“女生”;
(4)
解:由已知和(2)的结论知男生组的优秀率为65%,女生组的优秀率为70%,
(人),
因此估计该年级跳绳成绩优秀的总人数为149人.
【点睛】本题考查统计相关知识,掌握频数分布直方图、中位数的定义和应用,以及利用样本估计总体的方法是解题的关键.
27.(1);图见解析
(2)430
(3)3780000元
【分析】(1)根据信息b和所给频数直方图中数据得到数据在600≤x<800这一组的频数即可求解;
(2)根据中位数是将所给数据从小到大排好顺序后,排在最中间两个数据的平均数即可求解;
(3)用样本中的平均数估计为总体的平均数求解即可.
(1)
解:由信息b可知:400≤x<600这一组的频数为10,结合信息a,可得600≤x<800这一组的频数为:50-(10+13+10+3+2)=12.
∴600≤x<800这一组的频率为:.
补全频数分布直方图如下;
(2)
解:根据信息b和所给频数直方图中数据得到第25个和第26个数都为430,
∴中位数为=430(元),
故答案为:430;
(3)
解:由信息c可估计滑雪场游客消费额数据的每天平均数为420元,
∴估计滑雪场这个月(按30天计算)的游客消费总额420×300×30=3780000(元).
【点睛】本题考查频数直方图、中位数、用样本估计总体,理解题意,能从题意中获取有效信息是解答的关键.
28.(1)6,0.10
(2)见解析
(3)125
(4)60
【分析】(1)由40名乘以100≤x<120的频率可得m的值,用1减去其它组的频率可得k的值;
(2)求出n的值,根据m、n的值补全频数分布直方图即可;
(3)根据中位数的定义即可求解;
(4)利用样本估计总体即可求解.
(1)
解∶根据题意得∶,
;
故答案为∶6,0.10
(2)
解∶,
补全图形如下:
(3)
解:根据题意得: 位于样本中的第20,21位的数为125,125,
∴样本数据的中位数是;
故答案为:125
(4)
解:估计400名参与者中可获得表彰的有名,
故答案为:60
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,此外还利用了样本估计总体的思想.
29.(1)4,0.15
(2)见解析
(3)169
(4)40
【分析】(1)根据频数=总数×频率可计算出a的值,根据频数频率÷总数可计算出b的值;
(2)根据a的值即可补全频数分布直方图;
(3)根据中位数的定义即可求解;
(4)根据样本估计总体即可求解.
(1)
解∶根据题意得:a=20×0.20=4;
;
(2)
解:补全频数分布直方图如下图:
(3)
解:20名男生身高数据从小到大排列,第10,11个数据是169,169,
∴样本数据中,男生身高的中位数是,
故答案为:169
(4)
解:估计该校八年级男生身高在170-175cm范围内的人数约为
160×0.25=40人,
故答案为:40.
【点睛】本题考查频数分布直方图、频数分布表、中位数、用样本估计总体,解答本题的关键是明确频数分布直方图的特点,利用数形结合的思想解答.
30.(1)30,31.5
(2)A
(3)70
【分析】(1)根据众数和中位数的概念求解可得;
(2)利用方差的意义解答即可得;
(3)利用样本估计总体思想求解可得.
【详解】(1)解:由条形统计图知:甲组产量的众数为30,
乙组产量第5个数是31,第6个数是32,
乙组产量的中位数为==31.5,
故答案为:30,31.5;
(2)甲=×(28×2+29×1+30×3+31×2+32×2)=30.1,
乙=×(26+27+28+30+31+32×2+33×2+34)=30.5,
由条形统计图得,甲组产量的波动较小,方差较小,产量更稳定,
所以应选择营养液A.
故答案为:A;
(3)估计长势良好的大约为100×=70(株),
故答案为:70.
【点睛】本题考查中位数、众数和方差以及条形统计图,解题的关键是掌握众数、中位数和方差的意义.
一、单选题
1.(2022春·北京西城·八年级统考期末)在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
2.(2022春·北京东城·八年级统考期末)一次数学测试,某小组名同学的成绩统计如下(有两个数据被遮盖):
组员 甲 乙 丙 丁 戊 平均成绩 众数
得分
则被遮盖的两个数据依次是( )
A. B. C. D.
3.(2022春·北京朝阳·八年级统考期末)某农民统计了自己养鸡场1000只鸡出售时质量的数据,如下表:
质量/kg 1.0 1.2 1.5 1.8 2.0
频数 108 226 325 245 96
这组数据的众数是( )
A.1.0 B.1.5 C.1.8 D.2.0
4.(2022春·北京丰台·八年级统考期末)一家鞋店在某种运动鞋进货的过程中,商家关注的是卖出的这种运动鞋尺码组成的一组数据的( )
A.平均数 B.中位数 C.众数 D.方差
5.(2022春·北京海淀·八年级统考期末)下表记录了四名同学最近几次一分钟踢毽子选拔赛成绩的平均数与方差.
姓名 甲 乙 丙 丁
平均数 74.25 70 70 65.75
方差 3.07 4.28 2.57 6.78
根据表中数据,要从中选择两名成绩更好且发挥稳定的同学参加正式比赛,应选择( )
A.甲和乙 B.乙和丙 C.甲和丁 D.甲和丙
6.(2022春·北京石景山·八年级统考期末)甲、乙两名运动员的8次射击成绩(单位:环)如下图所示:
甲、乙射击成绩的方差分别为,则与的关系为( )
A. B. C. D.无法确定
7.(2022春·北京顺义·八年级统考期末)如果一组数据,,…,的平均数为,方差为,则数据,,…,的平均数和方差分别是( )
A. , B. , C. , D. ,
8.(2022秋·北京海淀·八年级校考期末)“实际平均续航里程”是指电动汽车的行驶总里程与充电次数的比值,是反映电动汽车性能的重要指标.某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程”,收集了使用该型号电动汽车1年以上的部分客户的相关数据,按年龄不超过40岁和年龄在40岁以上将客户分为两组,从组各抽取10位客户的电动汽车的“实际平均续航里程”数据整理成下图,其中“⊙”表示组的客户,“*”表示组的客户.
下列推断不正确的是( )
A.组客户的电动汽车的“实际平均续航里程”的最大值低于组
B.组客户的电动汽车的“实际平均续航里程”的方差低于组
C.组客户的电动汽车的“实际平均续航里程”的平均值低于组
D.这20位客户的电动汽车的“实际平均续航里程”的中位数落在组
9.(2022春·北京房山·八年级统考期末)下列几个常见统计量中能够反映一组数据变化范围大小的是( )
A.方差 B.中位数 C.众数 D.极差
10.(2022春·北京房山·八年级统考期末)为庆祝中国共产主义青年团成立100周年,某区举办了团课知识竞赛,甲、乙两所中学各派5名学生参加,两队学生的竞赛成绩如图所示,下列关系完全正确的是( )
A., B.,
C., D.,
11.(2022春·北京大兴·八年级统考期末)某校学生参加区诗词大赛预选赛,经过多次测试后,有四位同学成为晋级的候选人,具体情况如下表,如果从这四位同学中选出一名总体水平高且成绩稳定的选手晋级,你会推荐( ).
甲 乙 丙 丁
平均分 94 94 92 92
方差 23 35 23 35
A.甲 B.乙 C.丙 D.丁
12.(2022春·北京延庆·八年级统考期末)下表记录了甲、乙、丙、丁四名跳高运动员最近10次训练成绩(单位:cm)的平均数与方差:
甲 乙 丙 丁
平均数 181 183 183 181
方差 1.6 3.4 1.6 3.4
要选择一名成绩好且发挥稳定的同学参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
13.(2022春·北京顺义·八年级统考期末)某校组织环保知识竞赛,为参加区级比赛做选手选拔工作,经过多次测试后,有4名同学成为区级参赛选手的候选人,具体情况如下表:
甲 乙 丙 丁
平均分 90 92 95 95
方差 36 32 21 33
如果从这4名同学中选出1位参加区级比赛(总体水平高且状态稳定),你会推荐( )
A.甲 B.乙 C.丙 D.丁
14.(2022春·北京门头沟·八年级统考期末)下表记录了甲、乙、丙、丁四名滑雪选手次测试成绩的平均数与方差:
甲 乙 丙 丁
平均数(分)
方差
要选择一名成绩较高且状态稳定的选手参加滑雪比赛,那么应该选择的选手是( )
A.甲 B.乙 C.丙 D.丁
二、填空题
15.(2022春·北京丰台·八年级统考期末)每年的4月23日是“世界读书日”,某校为了解4月份八年级学生的读书情况,随机调查了八年级50名学生读书的册数,数据整理如下:
册数 0 1 2 3 4
人数 9 3 20 15 3
由此估计该校八年级学生4月份人均读书______册.
16.(2022春·北京海淀·八年级统考期末)某班有10名同学利用假期参与了社区志愿服务活动,他们的社区服务时长如下表所示.
服务时长(小时) 15 16 20
人数(人) 2 5 3
这10名同学社区服务的平均时长是______小时.
17.(2022春·北京·八年级统考期末)随着北京冬奥会的成功举办,越来越多的人喜欢上冰雪运动.为了解当地一家滑雪场的经营情况,小聪对该滑雪场自2022年1月31日至2月13日共两周的日接待游客数(单位:千人)进行了统计,并绘制成下面的统计图.
根据统计图提供的信息,有下列三个结论:
①按日接待游客数从高到低排名,2月6日在这14天中排名第4;
②记第一周,第二周日接待游客数的方差分别为s12,s22,则s12>s22;
③这14天日接待游客数的众数和中位数都是2.0千人.
其中所有正确结论的序号是______________.
18.(2022春·北京西城·八年级统考期末)射击运动员小东10次射击的成绩(单位:环):7.5,8,7.5,8.5,9,7,7,10,8.5,8.这10次成绩的平均数是8.1,方差是0.79,如果小东再射击一次,成绩为10环,则小东这11次成绩的方差______0.79.(填“大于”、“等于”或“小于”)
19.(2022春·北京东城·八年级统考期末)甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是,,,,则射击成绩最稳定的是______.(填“甲、乙、丙、丁”中的一位)
20.(2022春·北京朝阳·八年级统考期末)某市2021年和2022年5月1日至5日每日最高气温(单位:℃)如下表:
1日 2日 3日 4日 5日
2021年 22 22 24 24 25
2022年 27 26 31 33 30
则这五天的最高气温更稳定的是______年(填“2021”或“2022”).
21.(2022春·北京丰台·八年级统考期末)农科院为某地选择甲、乙两种甜玉米种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题,他们各用10块自然条件相同的试验田进行试验,下图是试验后得到的各试验田两种种子每公顷的产量(单位:t).已知甲、乙两种甜玉米种子的平均产量相差不大,那么由样本估计总体,推测这个地区比较适合种植______(填“甲”或“乙”)种甜玉米,理由是_____________________.
22.(2022春·北京通州·八年级统考期末)寒假期间,滑雪冬令营的同学们都参加了“单板滑雪”这个项目的40次的训练测试,每次测试成绩分别为5分,4分,3分,2分,1分五档,甲、乙两位同学在这个项目的测试成绩统计结果如图所示:
结合图中数据,请你从平均数、众数、中位数、方差中选择一方面评论一下两位同学的滑雪成绩_______.
三、解答题
23.(2022春·北京大兴·八年级统考期末)某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).
根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为________,图①中m的值为_______;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
24.(2022春·北京东城·八年级统考期末)为响应“带动三亿人参与冰雪运动”的号召,某校七、八年级举行了“冰雪运动知识竞赛”.为了解学生对冰雪运动知识的掌握情况,学校从两个年级分别随机抽取了20名学生的竞赛成绩(满分10分,6分及6分以上为合格)进行整理、描述和分析,下面给出了部分信息:
a.七年级20名学生的测试成绩为:
7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,7,9,7,10,6.
b.八年级20名学生的测试成绩条形统计图如图所示:
c.七、八年级抽取的学生的测试成绩的平均数、众数、中位数如下表所示:
年纪 平均数 众数 中位数
七年级 7.5 n 7
八年级 m 8 p
请你根据以上提供的信息,解答下列问题:
(1)上表中m=______,n=______,p=______;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生对冰雪运动知识掌握较好?请说明理由(写出一条理由即可);
(3)该校八年级共400名学生参加了此次测试活动,估计八年级参加此次测试活动成绩合格的学生人数.
25.(2022春·北京朝阳·八年级统考期末)为了解我国2022年25个地区第一季度快递业务收入情况,收集了这25个地区第一季度快递业务收入(单位:亿元)的数据,并对数据进行了整理、描述和分析,给出如下信息.
a.排在前5位的地区第一季度快递业务收入的数据分别为:
534.9 437.0 270.3 187.7 104.0
b.其余20个地区第一季度快递业务收入的数据的频数分布表如下:
快递业务收入x
频数 6 10 1 3
c.第一季度快递业务收入的数据在这一组的是:
20.2 20.4 22.4 24.2 26.1 26.5 28.5 34.4 39.1 39.8
d.排在前5位的地区、其余20个地区、全部25个地区第一季度快递业务收入的数据的平均数、中位数如下:
前5位的地区 其余20个地区 全部25个地区
平均数 306.8 29.9 n
中位数 270.3 m 28.5
根据以上信息,回答下列问题:
(1)表中m的值为______;
(2)在下面3个数中,与表中n的值最接近的是______(填写序号);
①30 ②85 ③150
(3)根据(2)中的数据,预计这25个地区2022年全年快递业务收入约为______亿元.
26.(2022春·北京丰台·八年级统考期末)2021年12月《北京市义务教育体育与健康考核评价方案》正式发布,跳绳成为新增的体育中考选考项目.某校体育组为了解八年级学生跳绳的基本情况,从八年级男、女生中各随机抽取了20名学生1分钟跳绳次数,并对数据进行整理、描述和分析.下面给出了部分信息.
a.学生1分钟跳绳次数频数分布直方图如下(数据分成9组:,,…,):
b.男生1分钟跳绳次数在这一组的是:140,141,142,143,144,145,145,147
c.1分钟跳绳次数的平均数、中位数、优秀率如下表:
组别 平均数 中位数 优秀率
男生 139 m 65%
女生 135 138 n
注:《国家中学生体质健康标准》规定:八年级男生1分钟跳绳次数大于或等于135个,成绩为优秀;八年级女生1分钟跳绳次数大于或等于130个,成绩为优秀.
根据以上信息,回答下列问题:
(1)将女生1分钟跳绳次数频数分布直方图补充完整;
(2)写出表中m,n的值;
(3)此次测试中,某学生的1分钟跳绳次数为140个,这名学生的成绩排名超过同组一半的学生,判断该生属于______(填“男生”或“女生”)组;
(4)如果全年级男生人数为100人,女生人数为120人,请估计该年级跳绳成绩优秀的总人数.
27.(2022春·北京顺义·八年级统考期末)2022年北京冬奥会的举办促进了冰雪旅游,小明为了解寒假期间冰雪旅游的消费情况,从某滑雪场的游客中随机抽取了50人,获得了这些游客当天消费额(单位:元)的数据,并对数据进行整理、描述和分析.下面给出部分信息:
a.滑雪场游客消费额数据的频数分布直方图如下(数据分成6组:0≤x<200,200≤x<400,400≤x<600,600≤x<800,800≤x<1000,1000≤x<1200):
b.滑雪场游客消费额数据在400≤x<600这一组的是:410 430 430 440 440 440 450 450 520 540
c.滑雪场游客消费额数据的平均数为420元.
根据以上信息,解决下列问题:
(1)求滑雪场游客消费额数据在600≤x<800这一组的频率,并补全频数分布直方图;
(2)滑雪场游客消费额数据的中位数是 ;
(3)若滑雪场在寒假期间的一个月内日均游客人数为300人,估计滑雪场这个月(按30天计算)的游客消费总额.
28.(2022春·北京房山·八年级统考期末)居家学习期间,为提高学生的身体素质,某中学开展了以“运动战疫情,跳出我青春”为主题的线上跳绳比赛,同学们通过拍摄视频的方式记录下1分钟内的跳绳个数.该学校共有400名同学参加了本次活动,我们从中随机抽取了40名同学的1分钟跳绳个数作为成绩数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.40名同学1分钟跳绳成绩的频数分布表和频数分布直方图如下:
40名同学1分钟跳绳成绩的频数分布表(表1)
跳绳成绩x(个) 频数 频率
2 0.05
8 0.20
m 0.15
8 0.20
n k
6 0.15
6 0.15
合计 40 1.00
b.40名同学1分钟跳绳成绩在这一组的数据如下表(表2)所示:
跳绳成绩(个) 120 125 128 135
频数 3 2 1 2
根据以上信息,回答下列问题:
(1)表1中m的值为______;k的值为______.
(2)补全该校40名学生1分钟跳绳成绩频数分布直方图.
(3)样本数据的中位数是_______.
(4)学校准备对1分钟跳绳成绩“不少于180个”以上的同学进行表彰,通过分析样本数据,估计400名参与者中可获得表彰的有______名.
29.(2022春·北京平谷·八年级统考期末)为了了解某中学八年级160名男生的身体发育情况,从中随机抽取了20名男生的身高进行测量,并对数据进行了整理、描述和分析,下面给出了部分信息.
a.20名男生身高数据如下(单位:cm):168 161 157 165 173 173 166 176 167 174 176 161 173 171 179 169 169 177 162 155
b.经分组整理后的频数分布表与频数分布直方图如图所示:
分组身高x厘米 频数 频率
155≤ x < 160 2 0.10
160≤ x < 165 3 b
165≤ x < 170 6
170≤ x < 175 0.25
175≤ x < 180 a 0.20
合计 20 1
但在列表和画图时,遗漏了频数分布表中的数据和频数分布直方图中相应的条形图.请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)样本数据中,男生身高的中位数是
(4)估计该校八年级男生身高在170-175cm范围内的人数约为
30.(2022春·北京海淀·八年级统考期末)为比较营养液A和营养液B对某种小西红柿产量的影响,甲、乙两个生物小组各选取了10株长势相近的小西红柿秧苗进行对照实验,甲组使用营养液A,乙组使用营养液B.将每株的产量记录整理,并绘制了如下两个条形图.
解答下列问题:
(1)甲组产量的众数为______,乙组产量的中位数为_______;
(2)经过计算发现两组产量的平均数接近,为了使产量更稳定,则应选择营养液______(填“A”或“B”);
(3)产量30个及以上为秧苗长势良好.现在选用第(2)问推荐的营养液培育100株秧苗,请估计长势良好的大约为______株.
参考答案:
1.B
【分析】由于比赛取前5名参加决赛,共有11名选手参加,根据中位数的意义分析即可.
【详解】11个不同的成绩按从小到大排序后,中位数及中位数之后的共有5个数,
故只要知道自己的成绩和中位数就可以知道是否进入决赛了.
故选B.
【点睛】本题考查了中位数意义.解题的关键是正确的求出这组数据的中位数.
2.A
【分析】根据平均数的计算公式先求出丙的得分,再根据方差公式进行计算即可得出答案.
【详解】根据题意得:
(分),
则丙的得分是分;
众数是,
故选A.
【点睛】考查了众数及平均数的定义,解题的关键是根据平均数求得丙的得分,难度不大.
3.B
【分析】出现次数最多的数据即为该组数据的众数,根据定义解答.
【详解】解:出现次数最多的是1.5,即这组数据的众数是1.5,
故选:B.
【点睛】此题考查了众数的定义,熟记定义是解题的关键.
4.C
【分析】商家关注的是哪种尺码销量最多,利用众数定义即可判断.
【详解】解:商家关注的是卖出的这种运动鞋中哪种尺码销量最多,
因此关注的是卖出的这种运动鞋尺码组成的一组数据的众数.
故选C.
【点睛】本题考查众数的应用,掌握众数的定义是解题的关键.
5.D
【分析】根据平均数和方差的意义判断即可.
【详解】解:由表知,甲、乙、丙成绩的平均数高,其中甲、丙成绩的方差小,
所以甲、丙成绩更好且发挥稳定,
故选:D.
【点睛】本题主要考查方差,解题的关键是掌握平均数及方差的意义.
6.C
【分析】结合图形,乙的成绩波动比较大,则波动大的方差就大.
【详解】解:从图看出:甲选手的成绩波动较小,说明它的成绩较稳定;乙选手的成绩的波动较大,则其方差大,即,
故选:C.
【点睛】此题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7.D
【分析】根据题目中的数据可以求得变化后的数据的平均数和方差,从而可以解答本题.
【详解】解:∵,,
∴变化后的数据的平均数为:,
方差为:,
故选:D.
【点睛】本题考查方差、算术平均数,解答本题的关键是明确题意,会计算一组数据的方差和平均数.
8.C
【分析】方差反应数据的波动程度,平均值容易受到最值影响,中位数需分数据为偶数个和奇数个讨论.
【详解】A.由图观察可知,A组的最大值再350km至400km之间,B组最大值再450km以上,故A正确;
B.由图观察可知,A组数据较为集中,B组数据较为分散,所以A组方差小于B组方差,故B正确;
C.由图观察可知,A组集中在300km和350km之间的有6人,250km至300km之间1人,200km至250km之间3人;而B组在300km至350km之间有3人,200km至250km之间有2人,低于200km的有3人,由此分析可知,A组客户的电动汽车的“实际平均续航里程”的平均值高于组,故C错误;
D.由于本组数据共计20个,采用第10个和第11个的平均数作为中位数,由此观察可知,这两个数在B组,故D正确
故选:C.
【点睛】熟练掌握平均数,中位数,方差的意义及影响要素是解题的关键.
9.D
【分析】根据极差是刻画数据离散程度的一个统计量.它能反映数据的波动范围大小解答;
【详解】解:在数据统计中,能反映一组数据变化范围大小的指标是极差,
故选:D.
【点睛】本题考查的是极差、方差、中位数、众数的概念和意义,掌握极差是刻画数据离散程度的一个统计量.它能反映数据的波动范围是解题的关键.
10.B
【分析】分别求出两所中学5名学生的成绩的平均数和方差,即可求解.
【详解】解:根据题意得:甲所中学5名学生的成绩为60,70,70,60,80,
乙所中学5名学生的成绩为70,80,80,70,90,
∴,,
56,
,
∴,.
故选:D
【点睛】本题主要考查了求平均数和方差,熟练掌握求平均数和方差的公式是解题的关键.
11.A
【分析】根据平均分及方差的比较即可求解.
【详解】解:甲的平均分=乙的平均分>丙和丁的平均分,
且,
因此甲的成绩最稳定,应推荐甲去,
故选:A.
【点睛】本题考查了根据方差判断一组数据的稳定性,熟练掌握方差越小越稳定是解题的关键.
12.C
【分析】平均数相同的情况下,根据方差越小,数据越稳定判断即可.
【详解】解:∵
∴从乙和丙中选一个,
∵,
∴丙的成绩方差最小,
∴应该选择丙.
故选:C.
【点睛】此题主要考查了方差和平均数,关键是掌握方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.平均数反映一组数据的一般水平,平均数较大的成绩相应的较好.
13.C
【分析】此题有两个要求:①成绩较好,②状态稳定.所以应选平均分数高、方差小的选手参赛,从而得出答案.
【详解】从表中可知:丙的方差最小、平均分最高,所以应推荐丙.
故选 C.
【点睛】本题考查平均数和方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
14.B
【分析】根据平均数的概念、方差的性质判断即可.
【详解】解:由表格中平均数可知:成绩好的选手是乙、丙,由表格中乙、丙的方差可知:成绩好且发挥稳定的选手是乙,
应该选择的选手是:乙,
故选:B.
【点睛】本题考查的是平均数、方差,解题的关键是掌握方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
15.2
【分析】先根据表格中的数据得出50名学生读书的总册数,然后除以50即可求出平均数.
【详解】解:估计该校八年级学生4月份人均读书(0×9+1×3+2×20+3×15+4×3)÷50=2(册),
由此估计该校八年级学生4月份人均读书2册.
故答案为:2.
【点睛】本题考查的是加权平均数的计算方法,通过样本去估计总体,总体平均数与样本平均数近似相等.
16.17
【分析】根据加权平均数的公式直接代入数据计算即可.
【详解】解:这10名同学社区服务的平均时长是:
=17(小时).
故答案为:17.
【点睛】本题考查了加权平均数,正确理解加权平均数的概念是解题的关键.
17.①②
【分析】①根据统计图数据判断即可;②根据数据的波动情况判断即可;③根据众数和中位数的定义判断即可.
【详解】解:①按日接待游客数从高到低排名,2月6日在这14天中排名第4,说法正确;
②记第一周,第二周日接待游客数的方差分别为s12,s22,则s12>s22,说法正确;
③这14天日接待游客数的众数为2.0千人,中位数为1.90千人,原说法错误.
所以正确结论的序号是①②.
故答案为:①②.
【点睛】本题考查了折线统计图,涉及中位数,方差,众数等知识.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
18.大于
【分析】计算小东这11次成绩的方差后比较即可.
【详解】解:小东这11次成绩的的平均成绩为(8.1×10+10)÷11=≈8.27,
小东这11次成绩的的方差S2=×[2×(7.5 8.27)2+2×(8 8.27)2+2×(8.5 8.27)2+2×(7 8.27)2+2×(10 8.27)2+(9 8.27)2]≈1.02,
即1.02>0.79,
∴小东这11次成绩的方差大于0.79,
故答案为:大于.
【点睛】本题考查求所给数据的方差:一般地设n个数据,x1,x2,…xn的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
19.丙
【分析】根据方差是用来衡量一组数据波动大小的量,故由甲乙丙丁的方差可直接作出判断.
【详解】解:∵,,,,
∴,
∴射击成绩最稳定的是丙.
故答案为:丙.
【点睛】本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
20.2021
【分析】分别计算出这两年的方差,即可判断.
【详解】解:2021年的平均数=23.4,方差==1.44,
2022年的平均数=,方差==6.64,
∵1.44<6.64,
∴2021年的最高气温更稳定,
故答案为:2021.
【点睛】此题考查了根据方差判断稳定性,正确掌握平均数的计算公式及方差的计算公式是解题的关键.
21. 甲 甲的产量比较稳定
【分析】据从图中数据的波动情况分析.
【详解】解:从图中看到,甲的波动比乙的波动小,故甲的产量比较稳定,
所以这个地区比较适合种植甲种甜玉米,理由是甲的产量比较稳定.
故答案为:甲;甲的产量比较稳定.
【点睛】本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
22.从平均数看甲同学成绩好(或从中位数看两个同学的成绩一样或从方差看乙的成绩稳定).答案不唯一
【分析】可以分别求出甲、乙两个同学的平均数、中位数和方差进行分析即可.
【详解】解:情况一:甲的平均数为:,
乙的平均数为:,
∵,
∴从平均数看甲同学成绩好.
情况二:甲的中位数为3,乙的中位数为3,因此从中位数看两个同学的成绩一样.
情况三:甲的方差为:
,
,
∵,
∴从方差看乙的成绩稳定.
故答案为:从平均数看甲同学成绩好(或从中位数看两个同学的成绩一样或从方差看乙的成绩稳定).答案不唯一
【点睛】本题主要考查了通过平均数、中位数、方差作出决策,解题的关键是求出两位同学的平均数、中位数和方差.
23.(Ⅰ)50,20;(Ⅱ)这组数据的平均数是5.9;众数为6;中位数为6.
【分析】(Ⅰ)利用用水量为5t的家庭个数除以其所占百分比即可求出本次接受调查的家庭个数;利用用水量为6.5t的家庭个数除以本次接受调查的家庭个数即得出其所占百分比,即得出m的值.
(Ⅱ)根据加权平均数的公式,中位数,众数的定义即可求出结果.
【详解】(Ⅰ)本次接受调查的家庭个数=,
由题意可知 ,
解得.
故答案为50,20.
(Ⅱ)观察条形统计图,
∵,
∴这组数据的平均数是5.9.
∵在这组数据中,6出现了16次,出现的次数最多,
∴这组数据的众数为6.
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数都是6,
即有,
∴这组数据的中位数为6.
【点睛】本题考查条形统计图与扇形统计图相关联,加权平均数,中位数以及众数.从条形统计图与扇形统计图中找到必要的数据和信息是解答本题的关键.
24.(1)7.5,7,7.5
(2)八年级,理由见解析
(3)360人
【分析】(1)根据平均数、众数、中位数的计算方法求解即可得出m、n、p的值;
(2)从中位数、众数的角度回答即可;
(3)求出七、八年级的总体合格率,利用总体乘以合格率计算即可即可.
(1)
解:由条形图得:(分),
七年级20名学生的测试成绩排序为:
5、5、6、6、6、7、7、7、7、7、7、8、8、8、9、9、9、9、10、10,
七年级学生成绩出现次数最多的是7分,共出现6次,因此七年级学生成绩的众数为7分,即n=7;
八年级学生成绩是20名学生测试成绩中位数位于,11两个位置数据的平均数,
从小到大排列后处在中间位置的两个数的测试成绩为7分,8分
平均数为(分),
因此八年级学生成绩的中位数是7.5分,即p=7.5;
故答案为:7.5,7,7.5;
(2)
解:根据表格七、八年级抽取的学生的测试成绩的平均数、众数、中位数如表所示:
年级 平均数 众数 中位数
七年级 7.5 7 7
八年级 7.5 8 7.5
∵七年八年学生测试成绩平均数相同,八年级学生测试成绩中位数与众数都比七年级学生测试成绩高
∴八年级学生掌握垃圾分类知识较好;
(3)
解:∵6分及6分以上为合格
七年级与八年级学生测试成绩合格人数分别为:18人,
占七八年各随机抽取20名学生的测试成绩的百分比为:
该校七、八年级共400名学生参加此次测试活动成绩合格的学生有(人),
答:我校七、八年级400名学生中测试成绩合格的大约有360人.
【点睛】本题考查了条形统计图、统计表,中位数、众数、平均数的意义,用样本的百分比含量估计总体中的数量,掌握中位数、平均数、众数、样本的百分比含量的计算方法是正确解答的前提.
25.(1)25.15
(2)②
(3)8528
【分析】(1)根据中位数的定义,计算第10个及第11个数据的平均数可得m;
(2)根据前5位的地区的平均数为306.8,其余20个地区的平均数为29.9,求出全部25个地区的收入,再除以25可得n,比较即可;
(3)用第一季度的总收入乘以4即可.
(1)
解:∵6+10=16,
∴其余20个地区的第一季度快递业务收入数据的第10个及第11个数据均在的范围,
∴第10个数据和第11个数据分别为24.2,26.1,
∴中位数m=,
故答案为:25.15;
(2)
∵前5位的地区的平均数为306.8,其余20个地区的平均数为29.9,
∴全部25个地区的收入=306.8×5+29.9×20=2132(亿元),
∴全部25个地区的n=2132÷25=85.28(亿元),
故选:②
(3)
这25个地区2022年全年快递业务收入约为2132×4=8528(亿元),
故答案为8528.
【点睛】此题考查了统计知识,求中位数,求平均数,根据部分的数量求总体,正确理解题意是解题的关键.
26.(1)见解析
(2),
(3)“女生”
(4)149人
【分析】(1)利用抽取女生的总人数和女生跳绳次数频数分布直方图中的数据,求出成绩在之间的人数即可;
(2)利用中位数的定义求m,利用八年级女生1分钟跳绳次数大于或等于130个的人数除以女生总人数求n;
(3)将这名学生的成绩与男生、女生成绩的中位数比较即可;
(4)利用样本估计总体的方法解决.
(1)
解:女生成绩在之间的人数为:,
补全后的频数分布直方图如下图所示:
(2)
解:由男生1分钟跳绳次数频数分布直方图和这一组的数据可知,20名男生中,成绩从低到高排序,第10位和第11位的成绩分别是141,142,
因此男生组的中位数:;
女生1分钟跳绳次数大于或等于130个的人数为:,
因此女生组的优秀率:,
故,;
(3)
解:这名学生的成绩140小于男生组的中位数141.5,大于女生组的中位数138,
因此该生属于“女生”,
故答案为:“女生”;
(4)
解:由已知和(2)的结论知男生组的优秀率为65%,女生组的优秀率为70%,
(人),
因此估计该年级跳绳成绩优秀的总人数为149人.
【点睛】本题考查统计相关知识,掌握频数分布直方图、中位数的定义和应用,以及利用样本估计总体的方法是解题的关键.
27.(1);图见解析
(2)430
(3)3780000元
【分析】(1)根据信息b和所给频数直方图中数据得到数据在600≤x<800这一组的频数即可求解;
(2)根据中位数是将所给数据从小到大排好顺序后,排在最中间两个数据的平均数即可求解;
(3)用样本中的平均数估计为总体的平均数求解即可.
(1)
解:由信息b可知:400≤x<600这一组的频数为10,结合信息a,可得600≤x<800这一组的频数为:50-(10+13+10+3+2)=12.
∴600≤x<800这一组的频率为:.
补全频数分布直方图如下;
(2)
解:根据信息b和所给频数直方图中数据得到第25个和第26个数都为430,
∴中位数为=430(元),
故答案为:430;
(3)
解:由信息c可估计滑雪场游客消费额数据的每天平均数为420元,
∴估计滑雪场这个月(按30天计算)的游客消费总额420×300×30=3780000(元).
【点睛】本题考查频数直方图、中位数、用样本估计总体,理解题意,能从题意中获取有效信息是解答的关键.
28.(1)6,0.10
(2)见解析
(3)125
(4)60
【分析】(1)由40名乘以100≤x<120的频率可得m的值,用1减去其它组的频率可得k的值;
(2)求出n的值,根据m、n的值补全频数分布直方图即可;
(3)根据中位数的定义即可求解;
(4)利用样本估计总体即可求解.
(1)
解∶根据题意得∶,
;
故答案为∶6,0.10
(2)
解∶,
补全图形如下:
(3)
解:根据题意得: 位于样本中的第20,21位的数为125,125,
∴样本数据的中位数是;
故答案为:125
(4)
解:估计400名参与者中可获得表彰的有名,
故答案为:60
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,此外还利用了样本估计总体的思想.
29.(1)4,0.15
(2)见解析
(3)169
(4)40
【分析】(1)根据频数=总数×频率可计算出a的值,根据频数频率÷总数可计算出b的值;
(2)根据a的值即可补全频数分布直方图;
(3)根据中位数的定义即可求解;
(4)根据样本估计总体即可求解.
(1)
解∶根据题意得:a=20×0.20=4;
;
(2)
解:补全频数分布直方图如下图:
(3)
解:20名男生身高数据从小到大排列,第10,11个数据是169,169,
∴样本数据中,男生身高的中位数是,
故答案为:169
(4)
解:估计该校八年级男生身高在170-175cm范围内的人数约为
160×0.25=40人,
故答案为:40.
【点睛】本题考查频数分布直方图、频数分布表、中位数、用样本估计总体,解答本题的关键是明确频数分布直方图的特点,利用数形结合的思想解答.
30.(1)30,31.5
(2)A
(3)70
【分析】(1)根据众数和中位数的概念求解可得;
(2)利用方差的意义解答即可得;
(3)利用样本估计总体思想求解可得.
【详解】(1)解:由条形统计图知:甲组产量的众数为30,
乙组产量第5个数是31,第6个数是32,
乙组产量的中位数为==31.5,
故答案为:30,31.5;
(2)甲=×(28×2+29×1+30×3+31×2+32×2)=30.1,
乙=×(26+27+28+30+31+32×2+33×2+34)=30.5,
由条形统计图得,甲组产量的波动较小,方差较小,产量更稳定,
所以应选择营养液A.
故答案为:A;
(3)估计长势良好的大约为100×=70(株),
故答案为:70.
【点睛】本题考查中位数、众数和方差以及条形统计图,解题的关键是掌握众数、中位数和方差的意义.
