人教版七年级数学 下册 第八章 8.1 二元一次方程 组 课件(共39张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第八章 8.1 二元一次方程 组 课件(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 15:31:06 | ||
图片预览










文档简介
(共32张PPT)
请同学们回想一下,什么是方程?
什么是一元一次方程?
只含有一个未知数(元),未知数的次数都是1, 且等号两边都是整式,这样的方程叫做一元一次方程.
如:
含有未知数的等式叫方程.
知识回顾
像这样,含有两个未知数,并且含有未知数的项的次数都是1的方程叫做二元一次方程.
请同学们观察一下这些式子有什么共同特点?
①
②
知识回顾
数学
七年级 下册
8.1 二元一次方程组
第八章 二元一次方程组
目标导航
1.了解二元一次方程(组)及其解的定义.
2.会检验一对数值是不是某个二元一次方程组的解.(重点)
3.能根据简单的实际问题列出二元一次方程组.(难点)
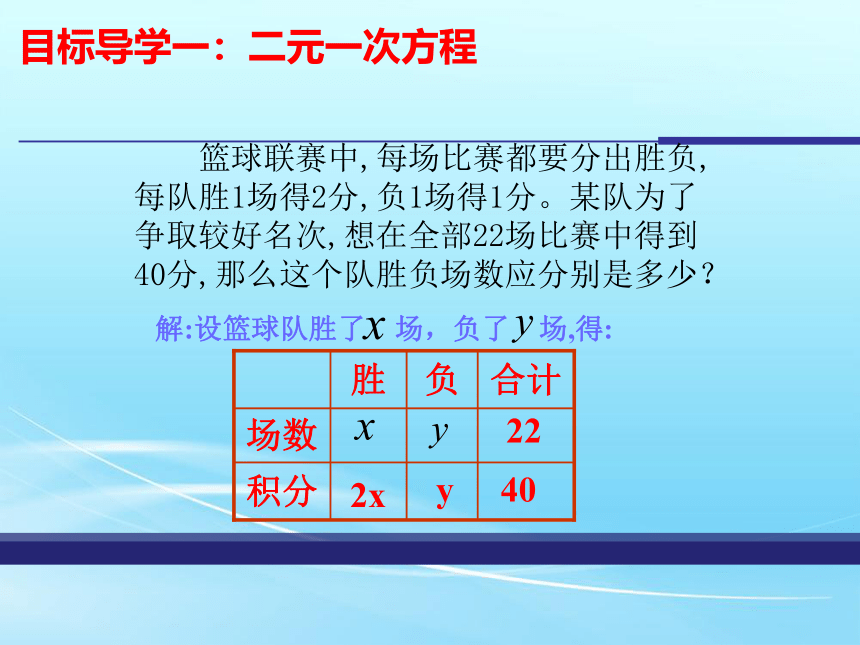
解:设篮球队胜了 场,负了 场,得:
积分
场数
合计
负
胜
22
2x
y
40
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分。某队为了争取较好名次,想在全部22场比赛中得到40分,那么这个队胜负场数应分别是多少?
目标导学一:二元一次方程
探究新知
解:设篮球队胜了 场,负了 场,得:
积分
22
场数
合计
负
胜
x+y=22
2x+y=40
2x
y
40
胜的场数+负的场数=总场数
胜场积分+负场积分=总积分
探究新知
议一议
思考一:上述方程有什么特点
思考二:它与你学过的一元一次方程比较
有什么区别
思考三:你能给它取名吗
思考四:你能给它下一个定义吗
x+y=22
2x+y=40
含有两个未知数,并且所含未知数的项的
次数都是1的方程叫做二元一次方程.
定义
探索新知
(1)二元一次方程的条件:
①整式方程;
②只含两个未知数;
③两个未知数系数都不为0;
④含有未知数的项的次数都是1.
(2)二元一次方程的一般形式:ax+by=c (a≠0,b≠0).
(8)4xy+5=0
(1)x+y=11
(3)x2+y=5
(4)3x-π=11
(5)-5x=4y+2
(7)7x+ =13
y
2
例1.判断下列方程是不是二元一次方程?
(2)m+1=2
(6)7+a=2b+11c
解:(1)(5)是二元一次方程.
总 结
判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都不为0且含未知数的项的次数都是1.
小试牛刀
请判断下列各方程中,哪些是二元一次方程,哪些不是?并说明理由。
含有两个未知数,每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.
问题 引言中的问题包含了两个必须同时满足的条件,也就是未知数x,y必须同时满足方程x+y=10和
2x+y=16.把两个方程合在一起,写成
就组成了一个方程组.这个方程组含有几个未知数?含有未知数的项的次数是多少?
二元一次方程组概念:
小试牛刀
3333的
3个未知数
3333的
次数是2
3333的
次数是2
练习 下列方程中是二元一次方程组的有:
二元一次方程的解:
定义:适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解.
目标导学二:二元一次方程的解
例 判断下列哪组未知数的值是二元一次方程
组 的解:( )
C
分析:二元一次方程的解是能使方程两边相等的一对未知数的值;因此将各个选项逐一代入原方程中,能使方程左右两边相等,则是方程的解,否则就不是方程的解.
总 结
(1)判断一组数值是不是方程的解,可将这组数值分别代入方程中,若满足该方程,则这组数值就是这个 方程的解,若不满足该方程,则这组数值就不是这个方程的解;
(2)二元一次方程中,如果已知其中一个未知数的值,我们可以利用二元一次方程的解的定义求出与它对应的另一个未知数的值.
二元一次方程的解和一元一次方程的解有什么区别?
一元一次方程的解 二元一次方程的解
一个
无数个
一个未知数的值
一对未知数的值
议一议
结论:二元一次方程有无数个解。
探索新知
把方程2x+2y =6改写成用含x 的式子表示y 的形式,得______________.
本题是将二元一次方程变形,用一个未知数表示另
一个未知数,可先移项,再系数化为1.把方程
2x+2y =6移项得:2y =6-2x,化简:y =3-x.
例
解析:
y=3-x
总 结
用含一个未知数的式子表示另一个未知数的变形步骤为:
(1)移项,把被表示项移到一边,把其他项移到另一边;
(2)化系数为1,在方程两边同除以被表示项的系数.
例 求二元一次方程3x+2y=12的非负整数解.
导引:对于二元一次方程3x+2y=12而言,它有无数组解,但它的非负整数解是有限的,可利用尝试取值的方法逐个验证.
解: 原方程可化为
因为x,y 都是非负整数,所以必须保证12-3x 能被2整除,
所以x 必为偶数.
探索新知
而由
所以x=0或2或4.
当x=0时,y=6;当x=2时,y=3;当x=4时,y=0,
所以原方程的非负整数解为
x≥0,得0≤x≤4,
总 结
求二元一次方程的整数解的方法:
(1)变形:把x 看成常数,把方程变形为用x表示y的形式;(2)划界:根据方程的解都是整数的特点,划定x的取值范围;
(3)试值:在x 的取值范围内逐一试值;
(4)确定:根据试值结果得到二元一次方程的整数解.其求解流程可概述为:变形
二元一次方程 二元一次方程组
定义
解的定义
解的情况 无数对 一对
如何判断
含有两个未知数(x和y),并且未知数的指数都是1,像这样的方程叫做二元一次方程.
把两个有共同未知数的二元一次方程合在一起,就组成了一个二元一次方程组.
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解
代入使方程成立
代入使方程成立
课堂小结
1.判断下列式子哪些是二元一次方程?
(1) 3x+5y=z
(5) x+y=12y
(3) x=―+1
2
y
(6)
(2) x2+y=0
(4) y+―x
2
1
√
y+―x=7
2
1
(7) xy+y=12
√
检测目标
2、下列方程组:(x、y 为未知数)
x+xy=3 2x+y=1 x=3 2x=2
⑴ ⑵ ⑶ ⑷
2x-y=3 y+z=2 y=4x - y=1
其中 ( )是二元一次方程组。
(3)(4)
检测目标
3.填表,使上下两对x,y的 值是
方程3 x+ y=5的解
x –2 0 0.4 2
y –0.5 –1 0 3
11
5
3.8
-1
11
6
2
5
3
3
2
检测目标
D.
x=4,
y=3
x=3,
y=6
x=2,
y=4
x=4,
y=2
A.
B.
C.
4.二元一次方程组
的解是( )
x+2y=10,
y=2x
C
检测目标
5.方程组
x-3y=2
2x-y=9
的解是上面的( )
B
检测目标
作 业 :
1.完成同步练习题
2.背诵知识点
谈谈你的收获吧
谢谢大家的努力
请同学们回想一下,什么是方程?
什么是一元一次方程?
只含有一个未知数(元),未知数的次数都是1, 且等号两边都是整式,这样的方程叫做一元一次方程.
如:
含有未知数的等式叫方程.
知识回顾
像这样,含有两个未知数,并且含有未知数的项的次数都是1的方程叫做二元一次方程.
请同学们观察一下这些式子有什么共同特点?
①
②
知识回顾
数学
七年级 下册
8.1 二元一次方程组
第八章 二元一次方程组
目标导航
1.了解二元一次方程(组)及其解的定义.
2.会检验一对数值是不是某个二元一次方程组的解.(重点)
3.能根据简单的实际问题列出二元一次方程组.(难点)
解:设篮球队胜了 场,负了 场,得:
积分
场数
合计
负
胜
22
2x
y
40
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分。某队为了争取较好名次,想在全部22场比赛中得到40分,那么这个队胜负场数应分别是多少?
目标导学一:二元一次方程
探究新知
解:设篮球队胜了 场,负了 场,得:
积分
22
场数
合计
负
胜
x+y=22
2x+y=40
2x
y
40
胜的场数+负的场数=总场数
胜场积分+负场积分=总积分
探究新知
议一议
思考一:上述方程有什么特点
思考二:它与你学过的一元一次方程比较
有什么区别
思考三:你能给它取名吗
思考四:你能给它下一个定义吗
x+y=22
2x+y=40
含有两个未知数,并且所含未知数的项的
次数都是1的方程叫做二元一次方程.
定义
探索新知
(1)二元一次方程的条件:
①整式方程;
②只含两个未知数;
③两个未知数系数都不为0;
④含有未知数的项的次数都是1.
(2)二元一次方程的一般形式:ax+by=c (a≠0,b≠0).
(8)4xy+5=0
(1)x+y=11
(3)x2+y=5
(4)3x-π=11
(5)-5x=4y+2
(7)7x+ =13
y
2
例1.判断下列方程是不是二元一次方程?
(2)m+1=2
(6)7+a=2b+11c
解:(1)(5)是二元一次方程.
总 结
判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都不为0且含未知数的项的次数都是1.
小试牛刀
请判断下列各方程中,哪些是二元一次方程,哪些不是?并说明理由。
含有两个未知数,每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.
问题 引言中的问题包含了两个必须同时满足的条件,也就是未知数x,y必须同时满足方程x+y=10和
2x+y=16.把两个方程合在一起,写成
就组成了一个方程组.这个方程组含有几个未知数?含有未知数的项的次数是多少?
二元一次方程组概念:
小试牛刀
3333的
3个未知数
3333的
次数是2
3333的
次数是2
练习 下列方程中是二元一次方程组的有:
二元一次方程的解:
定义:适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解.
目标导学二:二元一次方程的解
例 判断下列哪组未知数的值是二元一次方程
组 的解:( )
C
分析:二元一次方程的解是能使方程两边相等的一对未知数的值;因此将各个选项逐一代入原方程中,能使方程左右两边相等,则是方程的解,否则就不是方程的解.
总 结
(1)判断一组数值是不是方程的解,可将这组数值分别代入方程中,若满足该方程,则这组数值就是这个 方程的解,若不满足该方程,则这组数值就不是这个方程的解;
(2)二元一次方程中,如果已知其中一个未知数的值,我们可以利用二元一次方程的解的定义求出与它对应的另一个未知数的值.
二元一次方程的解和一元一次方程的解有什么区别?
一元一次方程的解 二元一次方程的解
一个
无数个
一个未知数的值
一对未知数的值
议一议
结论:二元一次方程有无数个解。
探索新知
把方程2x+2y =6改写成用含x 的式子表示y 的形式,得______________.
本题是将二元一次方程变形,用一个未知数表示另
一个未知数,可先移项,再系数化为1.把方程
2x+2y =6移项得:2y =6-2x,化简:y =3-x.
例
解析:
y=3-x
总 结
用含一个未知数的式子表示另一个未知数的变形步骤为:
(1)移项,把被表示项移到一边,把其他项移到另一边;
(2)化系数为1,在方程两边同除以被表示项的系数.
例 求二元一次方程3x+2y=12的非负整数解.
导引:对于二元一次方程3x+2y=12而言,它有无数组解,但它的非负整数解是有限的,可利用尝试取值的方法逐个验证.
解: 原方程可化为
因为x,y 都是非负整数,所以必须保证12-3x 能被2整除,
所以x 必为偶数.
探索新知
而由
所以x=0或2或4.
当x=0时,y=6;当x=2时,y=3;当x=4时,y=0,
所以原方程的非负整数解为
x≥0,得0≤x≤4,
总 结
求二元一次方程的整数解的方法:
(1)变形:把x 看成常数,把方程变形为用x表示y的形式;(2)划界:根据方程的解都是整数的特点,划定x的取值范围;
(3)试值:在x 的取值范围内逐一试值;
(4)确定:根据试值结果得到二元一次方程的整数解.其求解流程可概述为:变形
二元一次方程 二元一次方程组
定义
解的定义
解的情况 无数对 一对
如何判断
含有两个未知数(x和y),并且未知数的指数都是1,像这样的方程叫做二元一次方程.
把两个有共同未知数的二元一次方程合在一起,就组成了一个二元一次方程组.
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解
代入使方程成立
代入使方程成立
课堂小结
1.判断下列式子哪些是二元一次方程?
(1) 3x+5y=z
(5) x+y=12y
(3) x=―+1
2
y
(6)
(2) x2+y=0
(4) y+―x
2
1
√
y+―x=7
2
1
(7) xy+y=12
√
检测目标
2、下列方程组:(x、y 为未知数)
x+xy=3 2x+y=1 x=3 2x=2
⑴ ⑵ ⑶ ⑷
2x-y=3 y+z=2 y=4x - y=1
其中 ( )是二元一次方程组。
(3)(4)
检测目标
3.填表,使上下两对x,y的 值是
方程3 x+ y=5的解
x –2 0 0.4 2
y –0.5 –1 0 3
11
5
3.8
-1
11
6
2
5
3
3
2
检测目标
D.
x=4,
y=3
x=3,
y=6
x=2,
y=4
x=4,
y=2
A.
B.
C.
4.二元一次方程组
的解是( )
x+2y=10,
y=2x
C
检测目标
5.方程组
x-3y=2
2x-y=9
的解是上面的( )
B
检测目标
作 业 :
1.完成同步练习题
2.背诵知识点
谈谈你的收获吧
谢谢大家的努力
