2022—2023学年北师大版九年级数学下册第一章直角三角形的边角关系单元自测题(含答案)
文档属性
| 名称 | 2022—2023学年北师大版九年级数学下册第一章直角三角形的边角关系单元自测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 646.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 20:04:14 | ||
图片预览



文档简介
北师大版九年级数学下册第一章直角三角形的边角关系 单元自测题
一、单选题
1.如图,在 中, =3, =4, =5,则 的值是( )
A. B. C. D.
2.定义:圆心在原点,半径为1的圆称为单位圆.如图,已知点 在单位圆上,则 等于( )
A. B. C. D.
3.计算sin45°( )
A. B.1 C. D.
4.在Rt△ABC中,∠C=90°,如果∠A=α,AB=3,那么AC等于( )
A.3sinα B.3cosα C. D.
5.tan60°的值等于( )
A.1 B. C. D.2
6.在Rt△ABC中,∠C=90°,∠A=α,BC=m,则AB的长为( )
A.m sinα B. C.m cosα D.
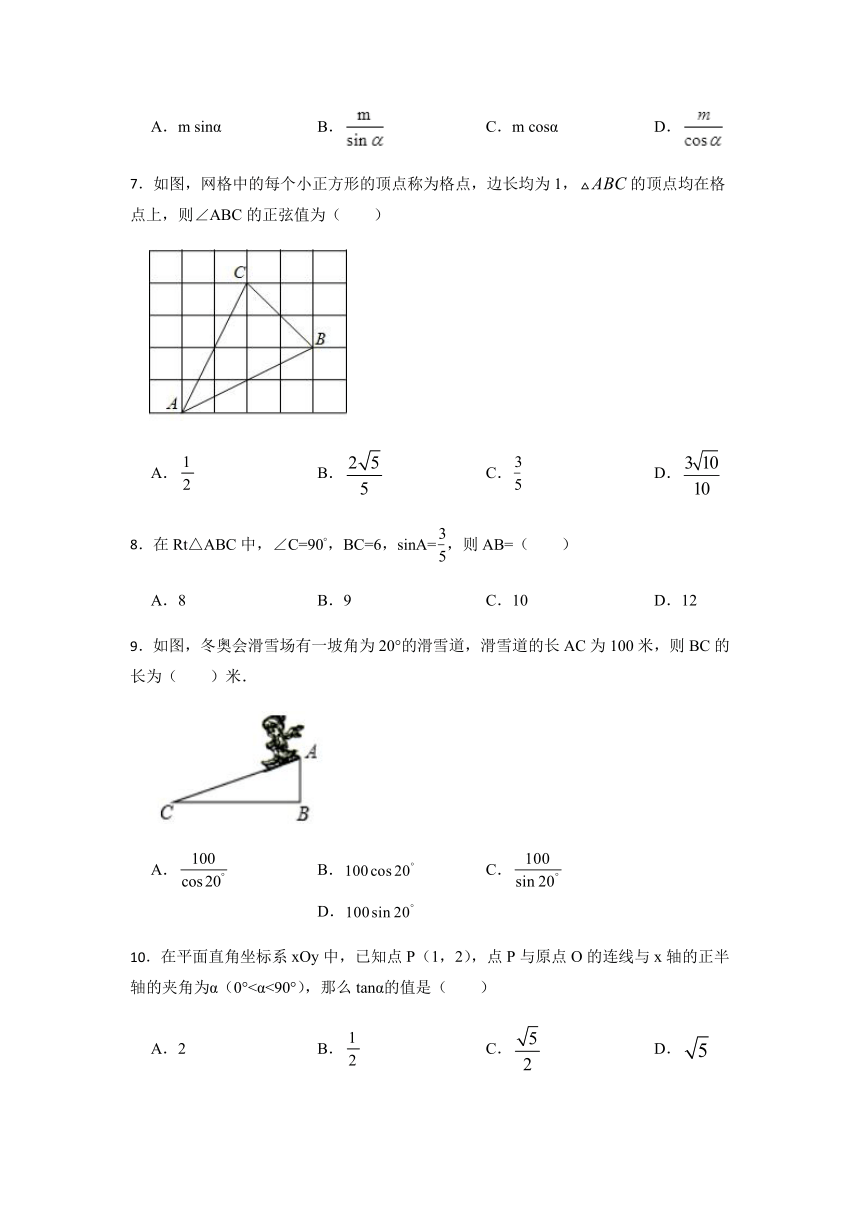
7.如图,网格中的每个小正方形的顶点称为格点,边长均为1,的顶点均在格点上,则∠ABC的正弦值为( )
A. B. C. D.
8.在Rt△ABC中,∠C=90°,BC=6,sinA=,则AB=( )
A.8 B.9 C.10 D.12
9.如图,冬奥会滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则BC的长为( )米.
A. B. C. D.
10.在平面直角坐标系xOy中,已知点P(1,2),点P与原点O的连线与x轴的正半轴的夹角为α(0°<α<90°),那么tanα的值是( )
A.2 B. C. D.
二、填空题
11.计算: –2cos60°= .
12. cos30°+ sin45°=
13.如图,在Rt△ABC中,∠ACB= 90°,CD⊥AB于点D, AD=, BD= ,则sinB= .
14.如图,已知斜坡AC的坡度i=1:2,小明沿斜坡AC从点A行进10m至点B,在这个过程中小明升高 m.
三、计算题
15.计算:
16.计算:.
四、解答题
17.今年五、六月份,我省各地、市普遭暴雨袭击,水位猛涨.某市抗洪抢险救援队伍在B处接到报告:有受灾群众被困于一座遭水淹的楼顶A处,情况危急!救援队伍在B处测得A在B的北偏东的方向上(如图所示),队伍决定分成两组:第一组马上下水游向A处救人,同时第二组从陆地往正东方向奔跑米到达C处,再从C处下水游向A处救人,已知A在C的北偏东的方向上,且救援人员在水中游进的速度均为1米/秒.在陆地上奔跑的速度为4米/秒,试问哪组救援队先到A处?请说明理由.(参考数据)
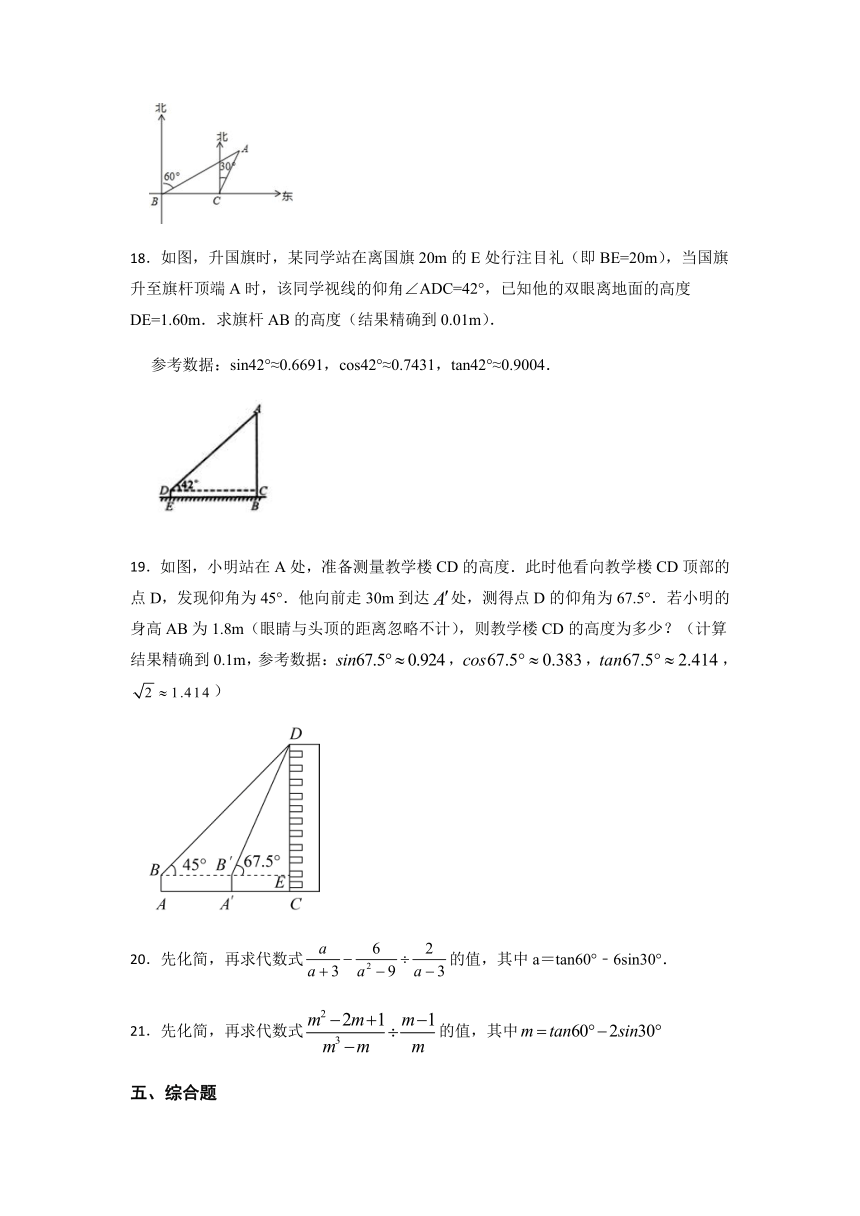
18.如图,升国旗时,某同学站在离国旗20m的E处行注目礼(即BE=20m),当国旗升至旗杆顶端A时,该同学视线的仰角∠ADC=42°,已知他的双眼离地面的高度DE=1.60m.求旗杆AB的高度(结果精确到0.01m).
参考数据:sin42°≈0.6691,cos42°≈0.7431,tan42°≈0.9004.
19.如图,小明站在A处,准备测量教学楼CD的高度.此时他看向教学楼CD顶部的点D,发现仰角为45°.他向前走30m到达处,测得点D的仰角为67.5°.若小明的身高AB为1.8m(眼睛与头顶的距离忽略不计),则教学楼CD的高度为多少?(计算结果精确到0.1m,参考数据:,,,)
20.先化简,再求代数式的值,其中a=tan60°﹣6sin30°.
21.先化简,再求代数式的值,其中
五、综合题
22.五一期间,数学兴趣小组的几位同学到公园游玩,看到公园内宝塔耸立,几人想用所学知识测量宝塔的高度.为此,他们在距离宝塔中心18m处(AC=18m)的一个斜坡CD上进行测量.如图,已知斜坡CD的坡度为i=1:,斜坡CD长12m,在点D处竖直放置测角仪DE,测得宝塔顶部B的仰角为37°,量得测角仪DE的高为1.5m,点A、B、C、D、E在同一平面内.
(1)求点D距地面的高度;
(2)求宝塔AB的高度.(结果精确到0.1,参考数据;sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,1.73)
23.如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,量得托板长,支撑板长,底座长,托板固定在支撑板顶端点处,且,托板可绕点转动,支撑板可绕点转动.(结果保留小数点后一位)(参考数据:,,,,)
(1)若,,求点到直线的距离;
(2)为了观看舒适,在(1)的情况下,把绕点逆时针旋转后,再将绕点顺时针旋转,使点落在直线上即可,求旋转的角度.
答案解析部分
1.【答案】A
【解析】【解答】解:在△ABC中,∵AC=3,BC=4,AB=5,又因32+42=52,即AC2+BC2=AB2,∴△ABC是直角三角形,且∠C=90°,∴tanB=.
故答案为:A.
【分析】首先根据勾股定理的逆定理判断出△ABC是直角三角形,再根据正切函数的定义即可得出答案.
2.【答案】B
【解析】【解答】解:过P作 于E,则PO=1,PE=y, OE=x,
∴ ,
故答案为:B.
【分析】过P作OA的垂线构造直角三角形,利用正弦的定义可得答案.
3.【答案】C
【解析】【解答】解:∵sin45°=.
故答案为:C.
【分析】根据特殊角的三角函数值即可求得答案.
4.【答案】B
【解析】【解答】解:如图,
∵ ,
∴AC=3cosα.
故答案为:B.
【分析】根据余弦等于邻边比斜边即可求解.
5.【答案】C
【解析】【解答】tan60°=。
故答案为:C。
【分析】根据30°、45°、60°特殊角的三角函数值解答即可。
6.【答案】B
【解析】【解答】解:在Rt△ABC中,
∵ ∠C=90°,∠A=α,BC=m,
∴sinα=,
∴AB=.
故答案为:B.
【分析】在Rt△ABC中,根据锐角三角函数正弦定义可得sinα=,由此即可求得答案.
7.【答案】D
【解析】【解答】解:如图,连接,
由勾股定理得,
∴
又
∴点E为BC的中点,
∴,
∴
∴
故答案为:D
【分析】连接AE,利用勾股定理求出AB和AE的长,再利用正弦的定义可得。
8.【答案】C
【解析】【解答】由题意得:sinA=,
∵BC=6,
∴,
∴AB=10,
故答案为:C.
【分析】根据sinA=,再将数据代入求出AB的长即可。
9.【答案】B
【解析】【解答】解:∵∠B=90°,∠C=20°,
∴,
∴BC=AC·=100.
故答案为:B.
【分析】根据余弦的定义得出,即可得出BC=100.
10.【答案】A
【解析】【解答】解:连接OP,过点P作PA⊥x轴,如图,
则,
∵点P(1,2),
∴,.
.
故答案为:A.
【分析】连接OP,过点P作PA⊥x轴,先求出,,再利用正切的定义可得。
11.【答案】0
【解析】【解答】 –2cos60°=1- .
故答案是:0.
【分析】根据零指数幂和特殊角的三角函数值可以解答.
12.【答案】
【解析】【解答】解: cos30°+ sin45°= ,
故答案为: .
【分析】利用特殊角的三角函数值进行计算即可.
13.【答案】
【解析】【解答】由AD=, BD= 得出AB=AD+BD=5,
由题意可知:∠ACB= 90°,CD⊥AB于点D,
由射影定理,
得出:
故答案为
【分析】利用已知条件求出AB的长,再利用射影定理求出AC的长,然后利用锐角三角函数的定义求出sinB的值.
14.【答案】
【解析】【解答】解:过点B作BD⊥水平面于点D,
∵斜坡AC的坡度i=1:2,
∴AD=2BD,
在Rt△ABD中,AD2+BD2=AB2,
即(2BD)2+BD2=102,
解得:BD=2,
∴在这个过程中小明升高了2m.
故答案为:2.
【分析】过点B作BD⊥水平面于点D,根据坡度可得AD=2BD,然后在Rt△ABD中,利用勾股定理即可求出BD,即小明升高的距离.
15.【答案】解:原式
【解析】【分析】先代入特殊锐角三角函数值,同时根据0指数幂的性质、二次根式的性质及绝对值的性质分别化简,再合并同类二次根式及进行有理数的加减法即可.
16.【答案】解:
=1-2+-2-2×
=1-2+-2-
=-3.
【解析】【分析】先算乘方和开方运算,同时化简绝对值,代入特殊角的三角函数值,再算乘法运算,然后合并即可.
17.【答案】解:过A作AD⊥BC,交BC的延长线于点D,
∵A在B北偏东60°方向上,
∴∠ABD=30°,
又∵A在C北偏东30°方向上,
∴∠ACD=60°,
又∵∠ABC=30°,所以∠BAC=30°,
∴∠ABD=∠BAC,所以AC=BC,
∵BC=120,所以AC=120,
在Rt△ACD中,∠ACD=60°,AC=120,
∴CD=60,AD=60,
在Rt△ABD中,∵∠ABD=30°,
∴AB=120,
第一组时间:≈207.84,
第二组时间:+=150,
因为207.84>150所以第二组先到达A处.
答:第二组先到.
【解析】【分析】过A作AD⊥BC,交BC的延长线于点D,在Rt△ACD中,由直角三角形的性质“30度角所对的的直角边等于斜边的一半”可得CD=AC,用勾股定理求得AD的值;在Rt△ABD中,同理可求得AB的值,分别计算两组队伍所用的时间,并比较大小即可判断求解.
18.【答案】解:由题意,得CD=BE=20(m),
在Rt△ACD中,AC=tan42°×CD≈0.9004×20≈18.0(m)
∵BC=DE=1.60(m),
∴AB=AC+BC=18.01+1.60=19.61(m)
【解析】【分析】由题意得CD=BE=20m,BC=DE=1.60m,再在Rt△ACD中,可得AC=tan42°·CD≈18.0m,最后由AB=AC+BC代入数据即可求得AB的高度.
19.【答案】解:如图,过点作,交BD于点F,
由题意可知四边形是矩形
∴.
∵,,
∴,
∴是∠BDC的角平分线
∵⊥DC,
∴,
∴.
∴,
∴.
答:教学楼CD的高为53.0m.
【解析】【分析】过点作,交BD于点F,利用解直角三角形的方法求出,求出,再利用线段的和差求出即可。
20.【答案】解:原式=﹣×
=﹣
=,
∵a=tan60°﹣6sin30°=﹣6×=﹣3,
∴原式===1﹣2.
【解析】【分析】先利用分式的混合运算化简,再利用特殊角的三角函数值求出a的值,最后将a的值代入计算即可。
21.【答案】解:
将代入上式,得:
【解析】【分析】先利用分式的混合运算化简,再利用特殊角的三角函数值求出m的值,最后将m的值代入计算即可。
22.【答案】(1)解:如图:
∵斜坡CD的坡度为i=1:,
∴在Rt△DCF中,tan∠DCF,
∴∠DCF=30°,
∴DFDC=6(m),
∴点D距地面的高度为6m
(2)解:过点E作EG⊥AB,垂足为G,
∴EG=AF,
∵∠DFC=90°,∠DCF=30°,
∴CFDF=6(m),
∵AC=18m,
∴AF=AC+CF=(18+6)m,
∴EG=(18+6)m,
在Rt△EBG中,∠BEC=37°,
∴BG=EG tan37°=(18+6)×0.75≈21.29(m),
∴BA=BG+ED+DF=21.29+1.5+6≈28.8(m),
∴宝塔AB的高度为28.8m.
【解析】【分析】(1)根据tan∠DCF,求出∠DCF=30°,再利用含30°角的直角三角形的性质可得DF的长;
(2)过点E作EG⊥AB,垂足为G,先利用线段的和差求出AF的长,再利用解直角三角形求出BG的长,最后利用线段的和差求出BA的长即可。
23.【答案】(1)解:如图所示,过点A作,,,
则,
∵,,
∴,
又∵,,
∴,,
∴,
∴,
∴,
又∵,,
∴mm,
∴.
∴点到直线的距离是.
(2)解:如图所示,
根据题意可得,,,
∴,
∴,
根据(1)可得,
∴旋转的角度=.
【解析】【分析】(1)过点A作,,,先求出,,再利用线段的和差求出AM的长即可;
(2)根据,求出,再利用角的运算求出旋转的角度即可。
一、单选题
1.如图,在 中, =3, =4, =5,则 的值是( )
A. B. C. D.
2.定义:圆心在原点,半径为1的圆称为单位圆.如图,已知点 在单位圆上,则 等于( )
A. B. C. D.
3.计算sin45°( )
A. B.1 C. D.
4.在Rt△ABC中,∠C=90°,如果∠A=α,AB=3,那么AC等于( )
A.3sinα B.3cosα C. D.
5.tan60°的值等于( )
A.1 B. C. D.2
6.在Rt△ABC中,∠C=90°,∠A=α,BC=m,则AB的长为( )
A.m sinα B. C.m cosα D.
7.如图,网格中的每个小正方形的顶点称为格点,边长均为1,的顶点均在格点上,则∠ABC的正弦值为( )
A. B. C. D.
8.在Rt△ABC中,∠C=90°,BC=6,sinA=,则AB=( )
A.8 B.9 C.10 D.12
9.如图,冬奥会滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则BC的长为( )米.
A. B. C. D.
10.在平面直角坐标系xOy中,已知点P(1,2),点P与原点O的连线与x轴的正半轴的夹角为α(0°<α<90°),那么tanα的值是( )
A.2 B. C. D.
二、填空题
11.计算: –2cos60°= .
12. cos30°+ sin45°=
13.如图,在Rt△ABC中,∠ACB= 90°,CD⊥AB于点D, AD=, BD= ,则sinB= .
14.如图,已知斜坡AC的坡度i=1:2,小明沿斜坡AC从点A行进10m至点B,在这个过程中小明升高 m.
三、计算题
15.计算:
16.计算:.
四、解答题
17.今年五、六月份,我省各地、市普遭暴雨袭击,水位猛涨.某市抗洪抢险救援队伍在B处接到报告:有受灾群众被困于一座遭水淹的楼顶A处,情况危急!救援队伍在B处测得A在B的北偏东的方向上(如图所示),队伍决定分成两组:第一组马上下水游向A处救人,同时第二组从陆地往正东方向奔跑米到达C处,再从C处下水游向A处救人,已知A在C的北偏东的方向上,且救援人员在水中游进的速度均为1米/秒.在陆地上奔跑的速度为4米/秒,试问哪组救援队先到A处?请说明理由.(参考数据)
18.如图,升国旗时,某同学站在离国旗20m的E处行注目礼(即BE=20m),当国旗升至旗杆顶端A时,该同学视线的仰角∠ADC=42°,已知他的双眼离地面的高度DE=1.60m.求旗杆AB的高度(结果精确到0.01m).
参考数据:sin42°≈0.6691,cos42°≈0.7431,tan42°≈0.9004.
19.如图,小明站在A处,准备测量教学楼CD的高度.此时他看向教学楼CD顶部的点D,发现仰角为45°.他向前走30m到达处,测得点D的仰角为67.5°.若小明的身高AB为1.8m(眼睛与头顶的距离忽略不计),则教学楼CD的高度为多少?(计算结果精确到0.1m,参考数据:,,,)
20.先化简,再求代数式的值,其中a=tan60°﹣6sin30°.
21.先化简,再求代数式的值,其中
五、综合题
22.五一期间,数学兴趣小组的几位同学到公园游玩,看到公园内宝塔耸立,几人想用所学知识测量宝塔的高度.为此,他们在距离宝塔中心18m处(AC=18m)的一个斜坡CD上进行测量.如图,已知斜坡CD的坡度为i=1:,斜坡CD长12m,在点D处竖直放置测角仪DE,测得宝塔顶部B的仰角为37°,量得测角仪DE的高为1.5m,点A、B、C、D、E在同一平面内.
(1)求点D距地面的高度;
(2)求宝塔AB的高度.(结果精确到0.1,参考数据;sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,1.73)
23.如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,量得托板长,支撑板长,底座长,托板固定在支撑板顶端点处,且,托板可绕点转动,支撑板可绕点转动.(结果保留小数点后一位)(参考数据:,,,,)
(1)若,,求点到直线的距离;
(2)为了观看舒适,在(1)的情况下,把绕点逆时针旋转后,再将绕点顺时针旋转,使点落在直线上即可,求旋转的角度.
答案解析部分
1.【答案】A
【解析】【解答】解:在△ABC中,∵AC=3,BC=4,AB=5,又因32+42=52,即AC2+BC2=AB2,∴△ABC是直角三角形,且∠C=90°,∴tanB=.
故答案为:A.
【分析】首先根据勾股定理的逆定理判断出△ABC是直角三角形,再根据正切函数的定义即可得出答案.
2.【答案】B
【解析】【解答】解:过P作 于E,则PO=1,PE=y, OE=x,
∴ ,
故答案为:B.
【分析】过P作OA的垂线构造直角三角形,利用正弦的定义可得答案.
3.【答案】C
【解析】【解答】解:∵sin45°=.
故答案为:C.
【分析】根据特殊角的三角函数值即可求得答案.
4.【答案】B
【解析】【解答】解:如图,
∵ ,
∴AC=3cosα.
故答案为:B.
【分析】根据余弦等于邻边比斜边即可求解.
5.【答案】C
【解析】【解答】tan60°=。
故答案为:C。
【分析】根据30°、45°、60°特殊角的三角函数值解答即可。
6.【答案】B
【解析】【解答】解:在Rt△ABC中,
∵ ∠C=90°,∠A=α,BC=m,
∴sinα=,
∴AB=.
故答案为:B.
【分析】在Rt△ABC中,根据锐角三角函数正弦定义可得sinα=,由此即可求得答案.
7.【答案】D
【解析】【解答】解:如图,连接,
由勾股定理得,
∴
又
∴点E为BC的中点,
∴,
∴
∴
故答案为:D
【分析】连接AE,利用勾股定理求出AB和AE的长,再利用正弦的定义可得。
8.【答案】C
【解析】【解答】由题意得:sinA=,
∵BC=6,
∴,
∴AB=10,
故答案为:C.
【分析】根据sinA=,再将数据代入求出AB的长即可。
9.【答案】B
【解析】【解答】解:∵∠B=90°,∠C=20°,
∴,
∴BC=AC·=100.
故答案为:B.
【分析】根据余弦的定义得出,即可得出BC=100.
10.【答案】A
【解析】【解答】解:连接OP,过点P作PA⊥x轴,如图,
则,
∵点P(1,2),
∴,.
.
故答案为:A.
【分析】连接OP,过点P作PA⊥x轴,先求出,,再利用正切的定义可得。
11.【答案】0
【解析】【解答】 –2cos60°=1- .
故答案是:0.
【分析】根据零指数幂和特殊角的三角函数值可以解答.
12.【答案】
【解析】【解答】解: cos30°+ sin45°= ,
故答案为: .
【分析】利用特殊角的三角函数值进行计算即可.
13.【答案】
【解析】【解答】由AD=, BD= 得出AB=AD+BD=5,
由题意可知:∠ACB= 90°,CD⊥AB于点D,
由射影定理,
得出:
故答案为
【分析】利用已知条件求出AB的长,再利用射影定理求出AC的长,然后利用锐角三角函数的定义求出sinB的值.
14.【答案】
【解析】【解答】解:过点B作BD⊥水平面于点D,
∵斜坡AC的坡度i=1:2,
∴AD=2BD,
在Rt△ABD中,AD2+BD2=AB2,
即(2BD)2+BD2=102,
解得:BD=2,
∴在这个过程中小明升高了2m.
故答案为:2.
【分析】过点B作BD⊥水平面于点D,根据坡度可得AD=2BD,然后在Rt△ABD中,利用勾股定理即可求出BD,即小明升高的距离.
15.【答案】解:原式
【解析】【分析】先代入特殊锐角三角函数值,同时根据0指数幂的性质、二次根式的性质及绝对值的性质分别化简,再合并同类二次根式及进行有理数的加减法即可.
16.【答案】解:
=1-2+-2-2×
=1-2+-2-
=-3.
【解析】【分析】先算乘方和开方运算,同时化简绝对值,代入特殊角的三角函数值,再算乘法运算,然后合并即可.
17.【答案】解:过A作AD⊥BC,交BC的延长线于点D,
∵A在B北偏东60°方向上,
∴∠ABD=30°,
又∵A在C北偏东30°方向上,
∴∠ACD=60°,
又∵∠ABC=30°,所以∠BAC=30°,
∴∠ABD=∠BAC,所以AC=BC,
∵BC=120,所以AC=120,
在Rt△ACD中,∠ACD=60°,AC=120,
∴CD=60,AD=60,
在Rt△ABD中,∵∠ABD=30°,
∴AB=120,
第一组时间:≈207.84,
第二组时间:+=150,
因为207.84>150所以第二组先到达A处.
答:第二组先到.
【解析】【分析】过A作AD⊥BC,交BC的延长线于点D,在Rt△ACD中,由直角三角形的性质“30度角所对的的直角边等于斜边的一半”可得CD=AC,用勾股定理求得AD的值;在Rt△ABD中,同理可求得AB的值,分别计算两组队伍所用的时间,并比较大小即可判断求解.
18.【答案】解:由题意,得CD=BE=20(m),
在Rt△ACD中,AC=tan42°×CD≈0.9004×20≈18.0(m)
∵BC=DE=1.60(m),
∴AB=AC+BC=18.01+1.60=19.61(m)
【解析】【分析】由题意得CD=BE=20m,BC=DE=1.60m,再在Rt△ACD中,可得AC=tan42°·CD≈18.0m,最后由AB=AC+BC代入数据即可求得AB的高度.
19.【答案】解:如图,过点作,交BD于点F,
由题意可知四边形是矩形
∴.
∵,,
∴,
∴是∠BDC的角平分线
∵⊥DC,
∴,
∴.
∴,
∴.
答:教学楼CD的高为53.0m.
【解析】【分析】过点作,交BD于点F,利用解直角三角形的方法求出,求出,再利用线段的和差求出即可。
20.【答案】解:原式=﹣×
=﹣
=,
∵a=tan60°﹣6sin30°=﹣6×=﹣3,
∴原式===1﹣2.
【解析】【分析】先利用分式的混合运算化简,再利用特殊角的三角函数值求出a的值,最后将a的值代入计算即可。
21.【答案】解:
将代入上式,得:
【解析】【分析】先利用分式的混合运算化简,再利用特殊角的三角函数值求出m的值,最后将m的值代入计算即可。
22.【答案】(1)解:如图:
∵斜坡CD的坡度为i=1:,
∴在Rt△DCF中,tan∠DCF,
∴∠DCF=30°,
∴DFDC=6(m),
∴点D距地面的高度为6m
(2)解:过点E作EG⊥AB,垂足为G,
∴EG=AF,
∵∠DFC=90°,∠DCF=30°,
∴CFDF=6(m),
∵AC=18m,
∴AF=AC+CF=(18+6)m,
∴EG=(18+6)m,
在Rt△EBG中,∠BEC=37°,
∴BG=EG tan37°=(18+6)×0.75≈21.29(m),
∴BA=BG+ED+DF=21.29+1.5+6≈28.8(m),
∴宝塔AB的高度为28.8m.
【解析】【分析】(1)根据tan∠DCF,求出∠DCF=30°,再利用含30°角的直角三角形的性质可得DF的长;
(2)过点E作EG⊥AB,垂足为G,先利用线段的和差求出AF的长,再利用解直角三角形求出BG的长,最后利用线段的和差求出BA的长即可。
23.【答案】(1)解:如图所示,过点A作,,,
则,
∵,,
∴,
又∵,,
∴,,
∴,
∴,
∴,
又∵,,
∴mm,
∴.
∴点到直线的距离是.
(2)解:如图所示,
根据题意可得,,,
∴,
∴,
根据(1)可得,
∴旋转的角度=.
【解析】【分析】(1)过点A作,,,先求出,,再利用线段的和差求出AM的长即可;
(2)根据,求出,再利用角的运算求出旋转的角度即可。
