2022-2023学年苏科版数学七年级下册第7章平面图形的认识(二)单元训练 (含答案)
文档属性
| 名称 | 2022-2023学年苏科版数学七年级下册第7章平面图形的认识(二)单元训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 902.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 20:01:35 | ||
图片预览


文档简介
第7章 平面图形的认识(二) 单元训练
一、单选题
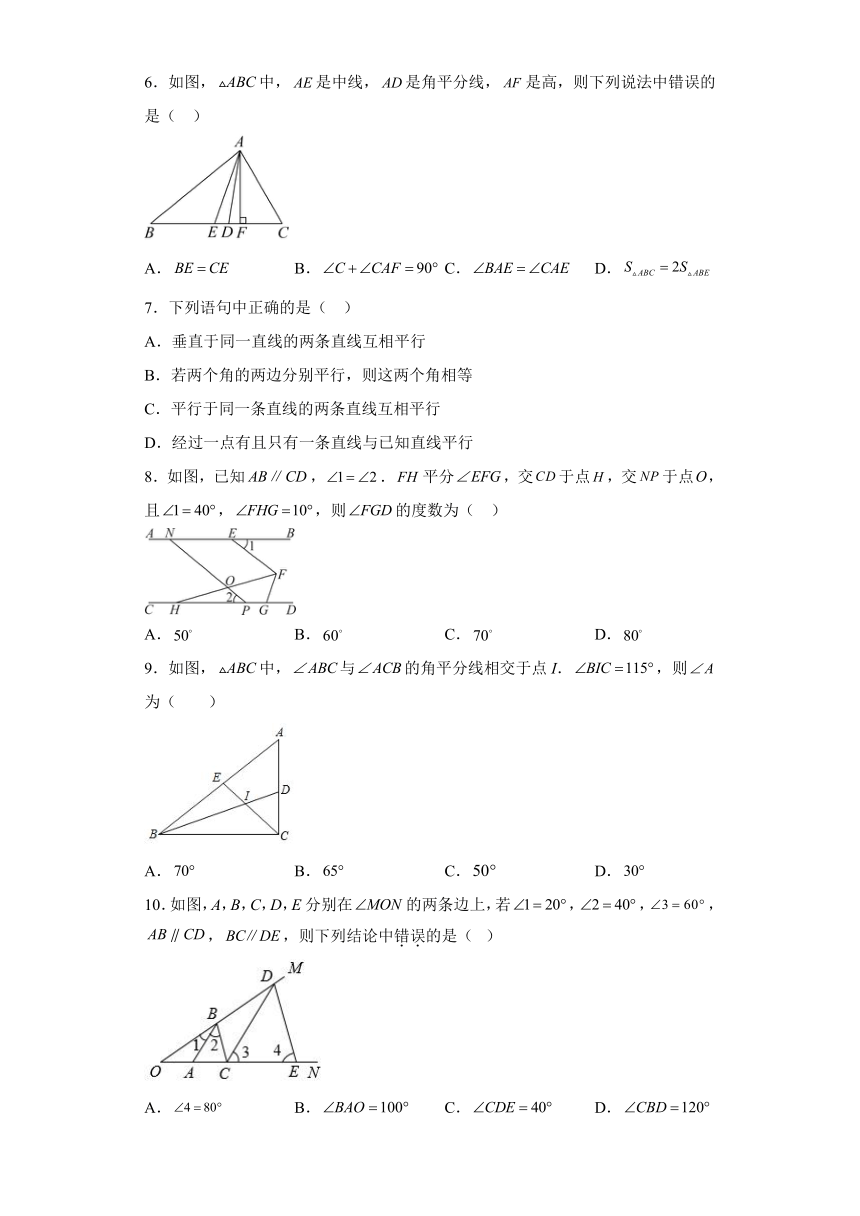
1.如图,下面给出四个判断:①和是同位角;②和是同位角;③和是同旁内角;④和是内错角.其中错误的是( )
A.①② B.①②③ C.②④ D.③④
2.下列长度的三条线段能组成三角形的是( )
A.2cm,2cm,5cm B.3cm,4cm,7cm
C.3cm,4cm,5cm D.5cm,5cm,11cm
3.如图,直线a,b被直线m所截,若,,则( )
A. B. C. D.
4.如图,小明从A点出发,沿直线前进9米后向左转,再沿直线前进9米,又向左转……照这样走下去,他第一次回到出发点A时,共走路程为( )
A.54米 B.72米 C.90米 D.108米
5.如图,点E在的延长线上,下列条件不能判定的是( )
B.
C. D.
6.如图,中,是中线,是角平分线,是高,则下列说法中错误的是( )
A. B. C. D.
7.下列语句中正确的是( )
A.垂直于同一直线的两条直线互相平行
B.若两个角的两边分别平行,则这两个角相等
C.平行于同一条直线的两条直线互相平行
D.经过一点有且只有一条直线与已知直线平行
8.如图,已知,.平分,交于点,交于点,且,,则的度数为( )
A. B. C. D.
9.如图,中,与的角平分线相交于点I.,则为( )
A. B. C. D.
10.如图,A,B,C,D,E分别在的两条边上,若,,,,,则下列结论中错误的是( )
A. B. C. D.
二、填空题
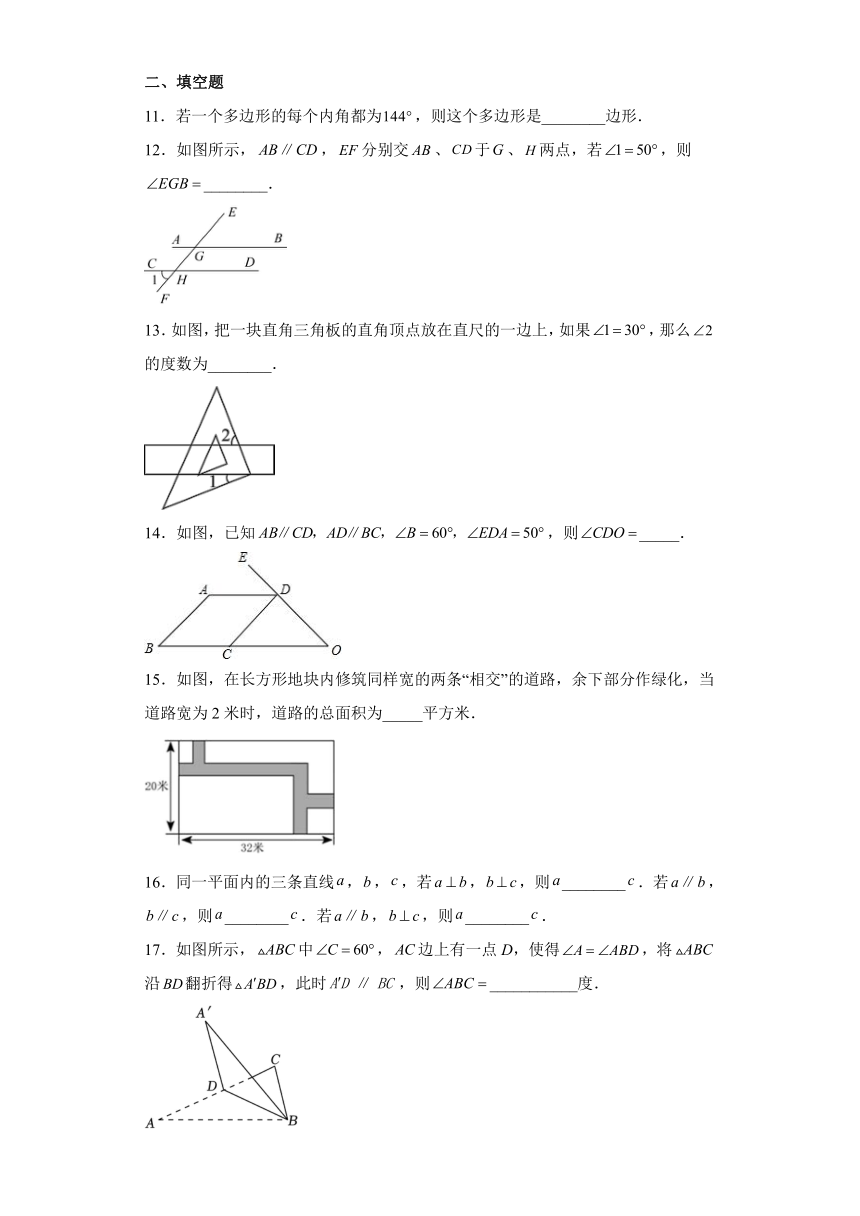
11.若一个多边形的每个内角都为,则这个多边形是________边形.
12.如图所示,,分别交、于、两点,若,则________.
13.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果,那么的度数为________.
14.如图,已知,则_____.
15.如图,在长方形地块内修筑同样宽的两条“相交”的道路,余下部分作绿化,当道路宽为2米时,道路的总面积为_____平方米.
16.同一平面内的三条直线,,,若,,则________.若,,则________.若,,则________.
17.如图所示,中,边上有一点D,使得,将沿翻折得,此时,则___________度.
18.两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到的位置,,,平移距离为,则阴影部分面积为__
三、解答题
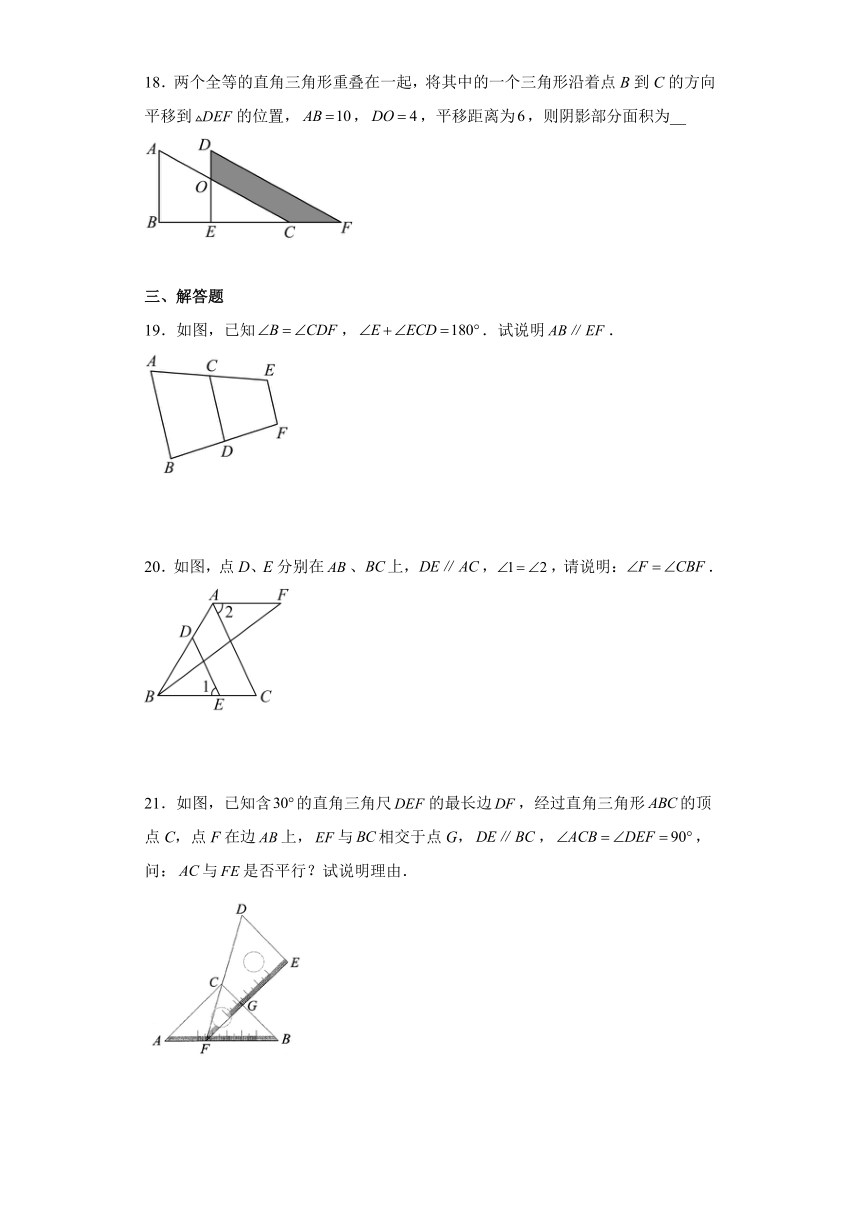
19.如图,已知,.试说明.
20.如图,点D、E分别在、上,,,请说明:.
21.如图,已知含的直角三角尺的最长边,经过直角三角形的顶点C,点F在边上,与相交于点G,,,问:与是否平行?试说明理由.
22.已知.
(1)如图1,求证:;
(2)若F为直线、之间的一点,,平分交于点G,交于点C.
①如图2,若,且,求的度数;
②如图3,若点K在射线上,且满足,若,,直接写出的度数.
23.已知:直线,M,N分别在直线,上,H为平面内一点,连,.
(1)如图1,延长至G,和的角平分线相交于点E.
①若,,则的度数为 ;
②探究与的数量关系,并给予证明;
(2)如图2,和的角平分线相交于点E.作平分,交的延长线于点Q,若,求的度数.
参考答案:
一、选择1.C2.C3.C4.B5.B6.C7.C8.B9.C10.B
二、填空11.十12.13.14.70°15.100
16. 17.9018.48
三、解答
19.【详解】解:∵,
∴(同位角相等,两直线平行),
∵,
∴(同旁内角互补,两直线平行),
∴(平行于同一条直线的两直线平行).
20.【详解】解:∵,
∴,(两直线平行,同位角相等),
∵,
∴,(等量代换),
∴,(内错角相等,两直线平行),
∴.(两直线平行,内错角相等).
21.【详解】解:.理由如下:
∵,
∴,
又∵,
∴,
∴.
22.【详解】(1)解:如图,
过E作,
∴,
又∵,
∴,
∴,
即;
(2)①如图,
过F作,交于H点,过点作,则,,
∵,
∴,
∴,
∵平分,
∴,
∵,
∴,
∵,
即,
∴,
∵,
∴,
即,
∴;
②如图,过点F作,
设,则,,
∴,
∴,,
当K在上,,
∴,
∴,
∴;
当K在延长线上时,,,
∴,
∴,
综上所述,或.
23.【详解】(1)①如图,过点E作交于点Q,
∵,,
∴,
又平分,
∴,
∴.
∴.
∵,.
∴.
∴,
即,
∵,
∴.
故答案为:;
②,理由详见①;
(2)过点H作,如答图2.
由(1)的证明方法可得,
由图可知,
∵,
∴,
∵,,
∴.
∴.
∴.
又∵,
∴.
即.
∵,
∴.
∴.
过点H作.
∵,
∴.
∴,
∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
一、单选题
1.如图,下面给出四个判断:①和是同位角;②和是同位角;③和是同旁内角;④和是内错角.其中错误的是( )
A.①② B.①②③ C.②④ D.③④
2.下列长度的三条线段能组成三角形的是( )
A.2cm,2cm,5cm B.3cm,4cm,7cm
C.3cm,4cm,5cm D.5cm,5cm,11cm
3.如图,直线a,b被直线m所截,若,,则( )
A. B. C. D.
4.如图,小明从A点出发,沿直线前进9米后向左转,再沿直线前进9米,又向左转……照这样走下去,他第一次回到出发点A时,共走路程为( )
A.54米 B.72米 C.90米 D.108米
5.如图,点E在的延长线上,下列条件不能判定的是( )
B.
C. D.
6.如图,中,是中线,是角平分线,是高,则下列说法中错误的是( )
A. B. C. D.
7.下列语句中正确的是( )
A.垂直于同一直线的两条直线互相平行
B.若两个角的两边分别平行,则这两个角相等
C.平行于同一条直线的两条直线互相平行
D.经过一点有且只有一条直线与已知直线平行
8.如图,已知,.平分,交于点,交于点,且,,则的度数为( )
A. B. C. D.
9.如图,中,与的角平分线相交于点I.,则为( )
A. B. C. D.
10.如图,A,B,C,D,E分别在的两条边上,若,,,,,则下列结论中错误的是( )
A. B. C. D.
二、填空题
11.若一个多边形的每个内角都为,则这个多边形是________边形.
12.如图所示,,分别交、于、两点,若,则________.
13.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果,那么的度数为________.
14.如图,已知,则_____.
15.如图,在长方形地块内修筑同样宽的两条“相交”的道路,余下部分作绿化,当道路宽为2米时,道路的总面积为_____平方米.
16.同一平面内的三条直线,,,若,,则________.若,,则________.若,,则________.
17.如图所示,中,边上有一点D,使得,将沿翻折得,此时,则___________度.
18.两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到的位置,,,平移距离为,则阴影部分面积为__
三、解答题
19.如图,已知,.试说明.
20.如图,点D、E分别在、上,,,请说明:.
21.如图,已知含的直角三角尺的最长边,经过直角三角形的顶点C,点F在边上,与相交于点G,,,问:与是否平行?试说明理由.
22.已知.
(1)如图1,求证:;
(2)若F为直线、之间的一点,,平分交于点G,交于点C.
①如图2,若,且,求的度数;
②如图3,若点K在射线上,且满足,若,,直接写出的度数.
23.已知:直线,M,N分别在直线,上,H为平面内一点,连,.
(1)如图1,延长至G,和的角平分线相交于点E.
①若,,则的度数为 ;
②探究与的数量关系,并给予证明;
(2)如图2,和的角平分线相交于点E.作平分,交的延长线于点Q,若,求的度数.
参考答案:
一、选择1.C2.C3.C4.B5.B6.C7.C8.B9.C10.B
二、填空11.十12.13.14.70°15.100
16. 17.9018.48
三、解答
19.【详解】解:∵,
∴(同位角相等,两直线平行),
∵,
∴(同旁内角互补,两直线平行),
∴(平行于同一条直线的两直线平行).
20.【详解】解:∵,
∴,(两直线平行,同位角相等),
∵,
∴,(等量代换),
∴,(内错角相等,两直线平行),
∴.(两直线平行,内错角相等).
21.【详解】解:.理由如下:
∵,
∴,
又∵,
∴,
∴.
22.【详解】(1)解:如图,
过E作,
∴,
又∵,
∴,
∴,
即;
(2)①如图,
过F作,交于H点,过点作,则,,
∵,
∴,
∴,
∵平分,
∴,
∵,
∴,
∵,
即,
∴,
∵,
∴,
即,
∴;
②如图,过点F作,
设,则,,
∴,
∴,,
当K在上,,
∴,
∴,
∴;
当K在延长线上时,,,
∴,
∴,
综上所述,或.
23.【详解】(1)①如图,过点E作交于点Q,
∵,,
∴,
又平分,
∴,
∴.
∴.
∵,.
∴.
∴,
即,
∵,
∴.
故答案为:;
②,理由详见①;
(2)过点H作,如答图2.
由(1)的证明方法可得,
由图可知,
∵,
∴,
∵,,
∴.
∴.
∴.
又∵,
∴.
即.
∵,
∴.
∴.
过点H作.
∵,
∴.
∴,
∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
