7.1.1 数系的扩充和复数的概念 课件(共22张PPT)
文档属性
| 名称 | 7.1.1 数系的扩充和复数的概念 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 22:31:31 | ||
图片预览








文档简介
7.1.1 数系的扩充和复数的概念
第七章 复数
2023/3/9
7.1.1 数系的扩充与复数的概念
创设情境 引入概念
它,曾是数学领域中一个飘荡了数百年的幽灵.
笛卡儿第一次提出了它的名字,却引来一片困惑,很多大数学家都不承认它.
欧拉说:“对于这类数,我们只能断言,它们既不是什么都不是,也不比什么都不是多些什么,更不比什么都不是少些什么,它们纯属虚幻.”
它的名字叫虚数.
我们知道,在实数范围内,解方程x2+1=0是无能为力的,只有把实数集扩充到复数集上才能解决,可是,历史上引进虚数,把实数集扩充到复数集可不是件容易的事.
16世纪意大利米兰学者卡当(1501~1576)在1545年发表的《重要的艺术》一书中,公布了三次方程的一般解法(“卡当公式”),他把10分成两部分,使它们的乘积等于40,即(5+?????????)(5-?????????)=40,尽管他认为(5+?????????)和(5-?????????)这两个表示式是没有意义的、想象的、虚无飘渺的.
?
随着科学和技术的进步,复数理论已越来越显出它的重要性,它不但对于数学本身的发展有着极其重要的意义,而且在系统分析、信号分析、量子力学、电工学、应用数学、流体力学、振动理论、机翼理论等方面得到了广泛应用,并在解决堤坝渗水的问题中显示了它的威力,也为建立巨大水电站提供了重要的理论依据.
同学们,你想了解复数的初步知识吗?那就让我们步入本章的学习吧!
引 入
数的扩充都是为了解决生产生活中的问题.
思考1 我们把一个数集连同规定的运算以及满足的运算律叫做一个数系.回顾从自然数系逐步到实数系的扩充过程,每一次数系扩充的主要原因是什么?
自然数集
整数集
有理数集
实数集
刻画相反意义的量
引入了
负数
解决测量等分问题
引入了
分数
解决度量正方体对角线等问题
引入了
无理数
计数的需要
引入了
自然数
?
从社会实践来看
引入
新数
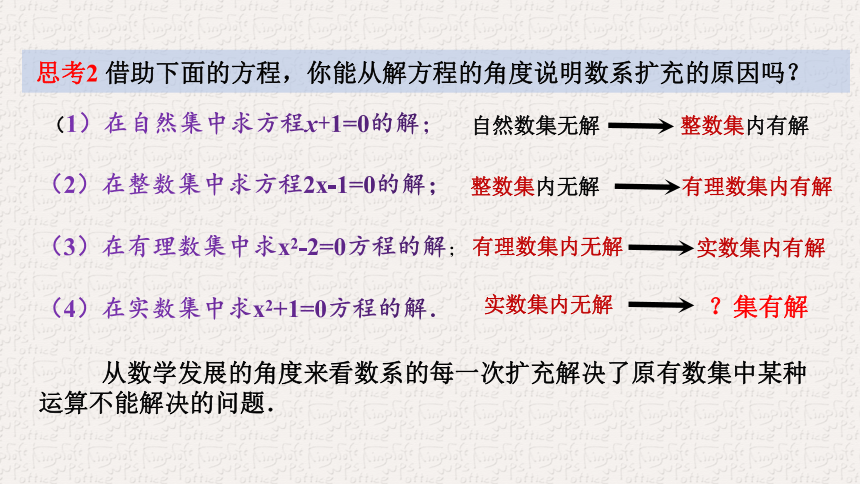
思考2 借助下面的方程,你能从解方程的角度说明数系扩充的原因吗?
从数学发展的角度来看数系的每一次扩充解决了原有数集中某种运算不能解决的问题.
(2)在整数集中求方程2x-1=0的解;
(3)在有理数集中求x2-2=0方程的解; ?
(4)在实数集中求x2+1=0方程的解.
?集有解
(1)在自然集中求方程x+1=0的解;
自然数集无解
整数集内有解
有理数集内有解
整数集内无解
有理数集内无解
实数集内有解
实数集内无解
探究新知
为了解决 这样的方程在实数系中无解的问题,我们设想引入一个新数i, 使得x=i是方程 的解, 即使得 i2 = -1.
i是数学家欧拉最早引入的,它取自imaginary
(想象的,假设的)一词的词头,i2=i·i.
思考3 数系扩充后,要遵循了什么规则?
如果没有运算,数只是孤立的符号!
数系扩充规则:数集扩充后,新数集中规定的加法和乘法运算,与原数集中规定的加法和乘法运算协调一致,并且加法和乘法都满足交换律和结合律,乘法对加法满足分配律.
依此规则,我们
①把实数b与i相乘,结果记作bi
②把实数a与bi相加,结果记作a+bi
所有实数以及i都可写成a+bi (a,b∈R)的形式,从而这些数都在扩充后的新数集中,我们把形如a+bi (a,b∈R)的数叫做复数.
1. 复数的概念
形如a+bi (a,b∈R)的数叫做复数.
i 叫做虚数单位.
全体复数所构成的集合C={a+bi |a,b∈R}叫做复数集.
复数通常用字母z表示,即
z=a+bi (a,b∈R)
2. 复数的代数形式
a叫做复数的实部
b叫做复数的虚部
注意:复数z的实部和虚部都是 数.
-3
实
1.复数i-2的虚部是( )
A.i B. -2 C.1 D.2
C
课堂练习
这些都叫复数,
课本P70第1题
有些是实数,
有些还能叫虚数,有些还能叫纯虚数
z=a+bi (a,b∈R)
当且仅当 b=0 时,它叫做
当且仅当 b≠0 时,它叫做
当且仅当a=b=0时,它是实数0;
z=a
z=0
z=a+bi (b≠0)
z=bi (b≠0)
虚数
实数
当且仅当 时,它叫做
a=0
b≠0
纯虚数
3. 复数的分类
复数
实数:
虚数:
纯虚数:
非纯虚数:
思考4 复数集C与实数集R之间有什么关系?
复
数
集
C
虚数集
实数集
R
纯虚数集
虚数
纯虚数
实数
课本P70第2题
课堂练习
探究新知
例1
解:当m-1=0时,即m=1时,复数z 是实数;
当m-1≠0时,即m≠1时,复数z 是虚数;
当m+1=0,且m-1≠0时,即m=-1时,复数z 是纯虚数.
课堂练习
4. 复数相等复数
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
即如果 ,那么
例2 求适合下列方程的实数x与y的值:
(1) (2)
课堂练习
例题讲解
例3
解:
练习6.若复数z=(m+1)+(m2-9)i<0,求实数m的值.
思考5 由3>2能否推出3十i>2+i?两个实数能比较大小,那么两个复数能比较大小吗?
由3>2不能推出3十i>2+i,
当两个复数都是实数时,可以比较大小,
当两个复数不全是实数时,不能比较大小.
m=-3
课堂练习
7.下列命题:
①若a∈R,则(a+1)i是纯虚数
②若a,b∈R,且a>b,则a+i>b+i
③若(x2-4)+(x2+3x+2)i是纯虚数,则实数x=±2
④实数集是复数集的真子集其中正确的是( )
A.① B.② C.③ D.④
D
课堂小结
1.虚数单位i的引入;
2.复数有关概念:
复数的代数形式:
复数的实部 、虚部
复数相等
虚数、纯虚数
THANKS
第七章 复数
2023/3/9
7.1.1 数系的扩充与复数的概念
创设情境 引入概念
它,曾是数学领域中一个飘荡了数百年的幽灵.
笛卡儿第一次提出了它的名字,却引来一片困惑,很多大数学家都不承认它.
欧拉说:“对于这类数,我们只能断言,它们既不是什么都不是,也不比什么都不是多些什么,更不比什么都不是少些什么,它们纯属虚幻.”
它的名字叫虚数.
我们知道,在实数范围内,解方程x2+1=0是无能为力的,只有把实数集扩充到复数集上才能解决,可是,历史上引进虚数,把实数集扩充到复数集可不是件容易的事.
16世纪意大利米兰学者卡当(1501~1576)在1545年发表的《重要的艺术》一书中,公布了三次方程的一般解法(“卡当公式”),他把10分成两部分,使它们的乘积等于40,即(5+?????????)(5-?????????)=40,尽管他认为(5+?????????)和(5-?????????)这两个表示式是没有意义的、想象的、虚无飘渺的.
?
随着科学和技术的进步,复数理论已越来越显出它的重要性,它不但对于数学本身的发展有着极其重要的意义,而且在系统分析、信号分析、量子力学、电工学、应用数学、流体力学、振动理论、机翼理论等方面得到了广泛应用,并在解决堤坝渗水的问题中显示了它的威力,也为建立巨大水电站提供了重要的理论依据.
同学们,你想了解复数的初步知识吗?那就让我们步入本章的学习吧!
引 入
数的扩充都是为了解决生产生活中的问题.
思考1 我们把一个数集连同规定的运算以及满足的运算律叫做一个数系.回顾从自然数系逐步到实数系的扩充过程,每一次数系扩充的主要原因是什么?
自然数集
整数集
有理数集
实数集
刻画相反意义的量
引入了
负数
解决测量等分问题
引入了
分数
解决度量正方体对角线等问题
引入了
无理数
计数的需要
引入了
自然数
?
从社会实践来看
引入
新数
思考2 借助下面的方程,你能从解方程的角度说明数系扩充的原因吗?
从数学发展的角度来看数系的每一次扩充解决了原有数集中某种运算不能解决的问题.
(2)在整数集中求方程2x-1=0的解;
(3)在有理数集中求x2-2=0方程的解; ?
(4)在实数集中求x2+1=0方程的解.
?集有解
(1)在自然集中求方程x+1=0的解;
自然数集无解
整数集内有解
有理数集内有解
整数集内无解
有理数集内无解
实数集内有解
实数集内无解
探究新知
为了解决 这样的方程在实数系中无解的问题,我们设想引入一个新数i, 使得x=i是方程 的解, 即使得 i2 = -1.
i是数学家欧拉最早引入的,它取自imaginary
(想象的,假设的)一词的词头,i2=i·i.
思考3 数系扩充后,要遵循了什么规则?
如果没有运算,数只是孤立的符号!
数系扩充规则:数集扩充后,新数集中规定的加法和乘法运算,与原数集中规定的加法和乘法运算协调一致,并且加法和乘法都满足交换律和结合律,乘法对加法满足分配律.
依此规则,我们
①把实数b与i相乘,结果记作bi
②把实数a与bi相加,结果记作a+bi
所有实数以及i都可写成a+bi (a,b∈R)的形式,从而这些数都在扩充后的新数集中,我们把形如a+bi (a,b∈R)的数叫做复数.
1. 复数的概念
形如a+bi (a,b∈R)的数叫做复数.
i 叫做虚数单位.
全体复数所构成的集合C={a+bi |a,b∈R}叫做复数集.
复数通常用字母z表示,即
z=a+bi (a,b∈R)
2. 复数的代数形式
a叫做复数的实部
b叫做复数的虚部
注意:复数z的实部和虚部都是 数.
-3
实
1.复数i-2的虚部是( )
A.i B. -2 C.1 D.2
C
课堂练习
这些都叫复数,
课本P70第1题
有些是实数,
有些还能叫虚数,有些还能叫纯虚数
z=a+bi (a,b∈R)
当且仅当 b=0 时,它叫做
当且仅当 b≠0 时,它叫做
当且仅当a=b=0时,它是实数0;
z=a
z=0
z=a+bi (b≠0)
z=bi (b≠0)
虚数
实数
当且仅当 时,它叫做
a=0
b≠0
纯虚数
3. 复数的分类
复数
实数:
虚数:
纯虚数:
非纯虚数:
思考4 复数集C与实数集R之间有什么关系?
复
数
集
C
虚数集
实数集
R
纯虚数集
虚数
纯虚数
实数
课本P70第2题
课堂练习
探究新知
例1
解:当m-1=0时,即m=1时,复数z 是实数;
当m-1≠0时,即m≠1时,复数z 是虚数;
当m+1=0,且m-1≠0时,即m=-1时,复数z 是纯虚数.
课堂练习
4. 复数相等复数
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
即如果 ,那么
例2 求适合下列方程的实数x与y的值:
(1) (2)
课堂练习
例题讲解
例3
解:
练习6.若复数z=(m+1)+(m2-9)i<0,求实数m的值.
思考5 由3>2能否推出3十i>2+i?两个实数能比较大小,那么两个复数能比较大小吗?
由3>2不能推出3十i>2+i,
当两个复数都是实数时,可以比较大小,
当两个复数不全是实数时,不能比较大小.
m=-3
课堂练习
7.下列命题:
①若a∈R,则(a+1)i是纯虚数
②若a,b∈R,且a>b,则a+i>b+i
③若(x2-4)+(x2+3x+2)i是纯虚数,则实数x=±2
④实数集是复数集的真子集其中正确的是( )
A.① B.② C.③ D.④
D
课堂小结
1.虚数单位i的引入;
2.复数有关概念:
复数的代数形式:
复数的实部 、虚部
复数相等
虚数、纯虚数
THANKS
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
