8.2 消元——解二元一次方程组第2课时加减消元法 课件(共21张PPT)
文档属性
| 名称 | 8.2 消元——解二元一次方程组第2课时加减消元法 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
二元一次方程组
8.2消元——解二元一次方程组第2课时加减消元法
教学目标/Teaching aims
1
掌握用加减消元法解二元一次方程组的步骤;
3
培养学生的分析能力,能迅速根据所给的二元一次方程组,选择一种简单的方法解方程组.
2
熟练运用消元法解简单的二元一次方程组;
复习回顾
问题1:
1. 解二元一次方程组的基本思路是什么?
1. 用代入法解二元一次方程组的一般步骤:
用代入法解二元一次方程组的关键是什么
基本思路:
二元
一元
消元
变
代
求
写
用含一个未知数的代数式表示另一个未知数.
复习回顾
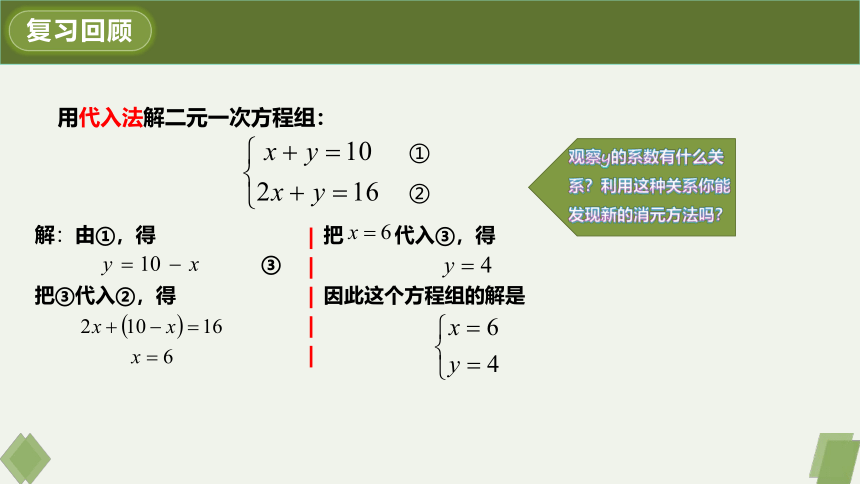
用代入法解二元一次方程组:
①
②
解:由①,得
把③代入②,得
把 代入③,得
因此这个方程组的解是
③
观察y的系数有什么关系?利用这种关系你能发现新的消元方法吗?
新知探究
①
②
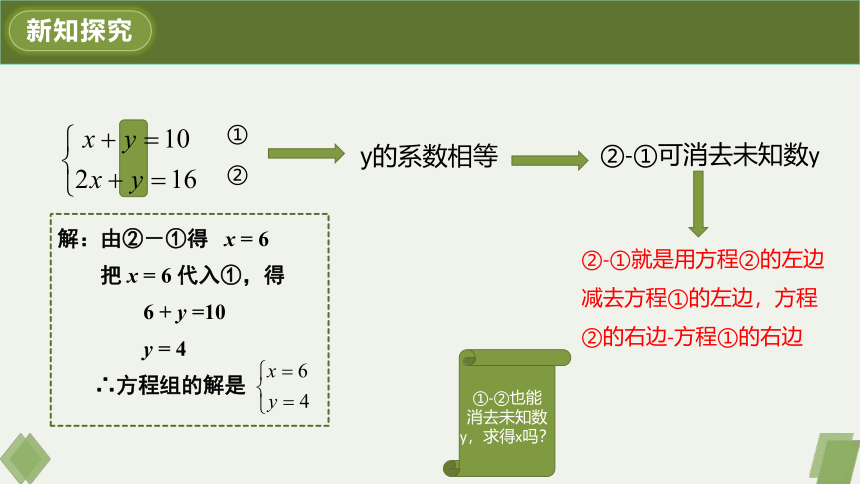
y的系数相等
②-①可消去未知数y
解:由②-①得 x = 6
把 x = 6 代入①,得
6 + y =10
y = 4
∴方程组的解是
②-①就是用方程②的左边减去方程①的左边,方程②的右边-方程①的右边
①-②也能消去未知数y,求得x吗?
新知探究
思考:
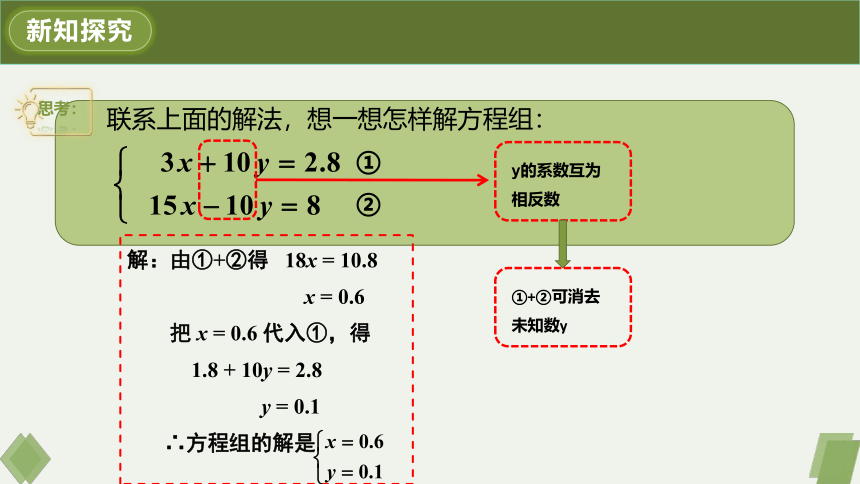
联系上面的解法,想一想怎样解方程组:
①
②
y的系数互为相反数
①+②可消去未知数y
解:由①+②得 18x = 10.8
x = 0.6
把 x = 0.6 代入①,得
1.8 + 10y = 2.8
y = 0.1
∴方程组的解是
归纳小结
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
解二元一次方程的基本思路:
消元,将二元转化为一元
同一未知数的系数 时,把两个方程的两边分别 !
互为相反数
相加
同一未知数的系数 时,把两个方程的两边分别 !
相等
相减
巩固练习
1. 用加减法解方程组
6x-5y=17②
应用( )
A.①-②消去y
B.①-②消去x
C. ②-①消去常数项
D. 以上都不对
B
6x+7y=-19①
巩固练习
①
②
3x+2y=23
5x+2y=33
2. 解方程组
解:
由②-①得:
将x=5代入①得:
15+2y=23
y=4.
所以原方程组的解是
x=5
y=4
2x=10
x=5.
巩固练习
3.用加减消元法解二元一次方程组
由①+②得 2x=11
x=5.5
把x=5.5代入①,得
5.5+y=7
y=1.5
∴方程组的解为
①
②
由① - ②得 2y=3
y=1.5
把y=1.5代入①,得
x+1.5=7
x=5.5
∴方程组的解为
消去 x
消去 y
新知探究
例3.
用加减法解方程组
3x+4y=16①
5x-6y=33②
同一个未知数的系数没有相反或者相等,直接加减这两个方程不能消元。
①+②得
①-②得
新知探究
思考:
1. 怎样将未知数的系数变成相等的或者相反数?
系数最小公倍数
消去 x
消去 y
解:由①×3得 9x + 12y =48 ③
由②×2得 10x - 12y =66 ④
③+④得 19x=114
x=6
把x=6代入①得y=-
所以这个方程组的解是
解:由①×5得 15x +20y =80 ③
由②×3得 15x- 18y =99 ④
③-④得 38y=-19
y=-
把y=- 代入①得x=6
所以这个方程组的解是
x=6
y=-
x=6
y=-
巩固练习
用加减消元法解方程组:
解:(1)由①+②得
把 代入①,得
因此这个方程组的解是
①
②
(1)
巩固练习
用加减消元法解方程组:
解:(2)由①×2得
由③-②,得
因此这个方程组的解是
①
②
③
把 代入①,得
(2)
归纳小结
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元:
消去一个元
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数;
当未知数系数的绝对值不同时,先利用等式的
性质将其化为相同即可.
用加减法解二元一次方程组:
课堂练习
1.用加减法解方程组:
①
②
①×3得:
所以原方程组的解是
解:
③-④得: y=2
把y=2代入①, 解得: x=3
②×2得:
6x+9y=36 ③
6x+8y=34 ④
课堂练习
解: ②×4得:
所以原方程组的解为
①
2.解方程组:
②
③
①+③得:7x = 35,
解得:x = 5.
把x = 5代入②得,y = 1.
4x-4y=16
课堂练习
3.已知x、y满足方程组 ,求代数式x-y的值.
解:
②-①得2x-2y=-1-5,
得x-y=-3.
①
②
课堂练习
4.甲乙二人同时解方程组 mx+y=5,
2x-ny=13
甲看错了m,解出的结果是 x=3.5,
y=-2
乙看错了n,解出的结果是 x=3,
y=-7
假设他们不再有其他错误,你能求出原方程组的解吗?
课堂总结
同一未知数的系数互为相反数→相加
同一未知数的系数相同→相减
既不相同也非相反数→找最小公倍数
基本思路:
二元
一元
消元
前提条件:
一般步骤:
变形
加减
求解
写解
加减消元法
8.2.2 解二元一次方程组(二)加减消元法
谢谢观看
二元一次方程组
二元一次方程组
8.2消元——解二元一次方程组第2课时加减消元法
教学目标/Teaching aims
1
掌握用加减消元法解二元一次方程组的步骤;
3
培养学生的分析能力,能迅速根据所给的二元一次方程组,选择一种简单的方法解方程组.
2
熟练运用消元法解简单的二元一次方程组;
复习回顾
问题1:
1. 解二元一次方程组的基本思路是什么?
1. 用代入法解二元一次方程组的一般步骤:
用代入法解二元一次方程组的关键是什么
基本思路:
二元
一元
消元
变
代
求
写
用含一个未知数的代数式表示另一个未知数.
复习回顾
用代入法解二元一次方程组:
①
②
解:由①,得
把③代入②,得
把 代入③,得
因此这个方程组的解是
③
观察y的系数有什么关系?利用这种关系你能发现新的消元方法吗?
新知探究
①
②
y的系数相等
②-①可消去未知数y
解:由②-①得 x = 6
把 x = 6 代入①,得
6 + y =10
y = 4
∴方程组的解是
②-①就是用方程②的左边减去方程①的左边,方程②的右边-方程①的右边
①-②也能消去未知数y,求得x吗?
新知探究
思考:
联系上面的解法,想一想怎样解方程组:
①
②
y的系数互为相反数
①+②可消去未知数y
解:由①+②得 18x = 10.8
x = 0.6
把 x = 0.6 代入①,得
1.8 + 10y = 2.8
y = 0.1
∴方程组的解是
归纳小结
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
解二元一次方程的基本思路:
消元,将二元转化为一元
同一未知数的系数 时,把两个方程的两边分别 !
互为相反数
相加
同一未知数的系数 时,把两个方程的两边分别 !
相等
相减
巩固练习
1. 用加减法解方程组
6x-5y=17②
应用( )
A.①-②消去y
B.①-②消去x
C. ②-①消去常数项
D. 以上都不对
B
6x+7y=-19①
巩固练习
①
②
3x+2y=23
5x+2y=33
2. 解方程组
解:
由②-①得:
将x=5代入①得:
15+2y=23
y=4.
所以原方程组的解是
x=5
y=4
2x=10
x=5.
巩固练习
3.用加减消元法解二元一次方程组
由①+②得 2x=11
x=5.5
把x=5.5代入①,得
5.5+y=7
y=1.5
∴方程组的解为
①
②
由① - ②得 2y=3
y=1.5
把y=1.5代入①,得
x+1.5=7
x=5.5
∴方程组的解为
消去 x
消去 y
新知探究
例3.
用加减法解方程组
3x+4y=16①
5x-6y=33②
同一个未知数的系数没有相反或者相等,直接加减这两个方程不能消元。
①+②得
①-②得
新知探究
思考:
1. 怎样将未知数的系数变成相等的或者相反数?
系数最小公倍数
消去 x
消去 y
解:由①×3得 9x + 12y =48 ③
由②×2得 10x - 12y =66 ④
③+④得 19x=114
x=6
把x=6代入①得y=-
所以这个方程组的解是
解:由①×5得 15x +20y =80 ③
由②×3得 15x- 18y =99 ④
③-④得 38y=-19
y=-
把y=- 代入①得x=6
所以这个方程组的解是
x=6
y=-
x=6
y=-
巩固练习
用加减消元法解方程组:
解:(1)由①+②得
把 代入①,得
因此这个方程组的解是
①
②
(1)
巩固练习
用加减消元法解方程组:
解:(2)由①×2得
由③-②,得
因此这个方程组的解是
①
②
③
把 代入①,得
(2)
归纳小结
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元:
消去一个元
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数;
当未知数系数的绝对值不同时,先利用等式的
性质将其化为相同即可.
用加减法解二元一次方程组:
课堂练习
1.用加减法解方程组:
①
②
①×3得:
所以原方程组的解是
解:
③-④得: y=2
把y=2代入①, 解得: x=3
②×2得:
6x+9y=36 ③
6x+8y=34 ④
课堂练习
解: ②×4得:
所以原方程组的解为
①
2.解方程组:
②
③
①+③得:7x = 35,
解得:x = 5.
把x = 5代入②得,y = 1.
4x-4y=16
课堂练习
3.已知x、y满足方程组 ,求代数式x-y的值.
解:
②-①得2x-2y=-1-5,
得x-y=-3.
①
②
课堂练习
4.甲乙二人同时解方程组 mx+y=5,
2x-ny=13
甲看错了m,解出的结果是 x=3.5,
y=-2
乙看错了n,解出的结果是 x=3,
y=-7
假设他们不再有其他错误,你能求出原方程组的解吗?
课堂总结
同一未知数的系数互为相反数→相加
同一未知数的系数相同→相减
既不相同也非相反数→找最小公倍数
基本思路:
二元
一元
消元
前提条件:
一般步骤:
变形
加减
求解
写解
加减消元法
8.2.2 解二元一次方程组(二)加减消元法
谢谢观看
二元一次方程组
