8.3 实际问题与二元一次方程组 课件(共30张PPT)
文档属性
| 名称 | 8.3 实际问题与二元一次方程组 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 13:49:44 | ||
图片预览











文档简介
(共30张PPT)
第八章
二元一次方程组
8.3实际问题与二元一次方程组
教学目标/Teaching aims
1
能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列出二元一次方程组并求解。
2
熟练运用消元法解简单的二元一次方程组。
复习回顾
思考:
列方程解应用题常用的几种数量关系:
(1)行程问题:
路程=速度×时间
顺水(风)速度=静水(风)速度+水(风)流速度
(2)工程问题:
工作量=工作效率×工作时间
复习回顾
(3)利息问题:
年利率=年利息÷本金×100%;
本息和=本金+利息;
总利润=每件商品的利润×销量.
(4)利润问题:
商品利润 = 商品售价 - 商品进价;
商品售价 = 标价×折扣数;
(商品利润=商品进价×商品利润率)
复习回顾
圆面积=πr2;
(5)面积问题:
矩形面积=长×宽;
平行四边形面积=底×高;
正方形面积=边长2;
三角形面积=底乘以高的一半;
新知探究
例1.养牛场原有30只母牛和15只小牛,1天约需用饲675kg;一周后又购进12只母牛和5只小牛,这时1天约需用饲料940kg.饲养员李大叔估计平均每只母牛1天约需饲料18~20kg,每只小牛1天约需饲料7~8kg.你能否通过计算检验他的估计?
1、怎样检验他的估计呢?
2、题目中包含怎样的等量关系?
新知探究
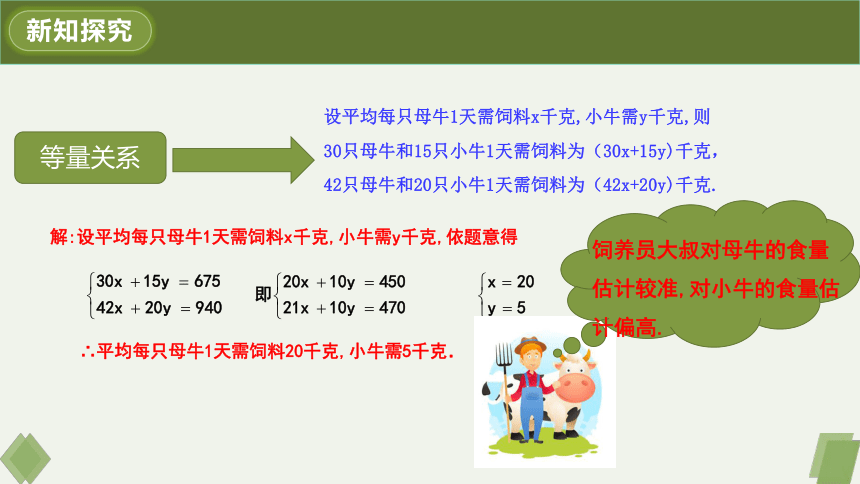
等量关系
设平均每只母牛1天需饲料x千克,小牛需y千克,则
30只母牛和15只小牛1天需饲料为(30x+15y)千克,
42只母牛和20只小牛1天需饲料为(42x+20y)千克.
解:设平均每只母牛1天需饲料x千克,小牛需y千克,依题意得
∴平均每只母牛1天需饲料20千克,小牛需5千克.
饲养员大叔对母牛的食量估计较准,对小牛的食量估计偏高.
巩固练习
巩固练习
新知探究
例2 据统计资料,甲、乙两种作物的单位面积产量的比 1:2. 现要把一块长 200 m ,宽 100 m 的长方形土地,分为两块小长方形土地,分别种植这两种作物. 怎样划分这块土地,使甲、乙两种作物的总产量的比是 3:4 ?
200 m
100 m
总产量 = 单位面积产量×面积
新知探究
① 种植方案为:甲、乙两种作物的种植区域分别为长方形AEFD和BCFE.此时设 AE=x m ,BE= y m,根据问题中涉及长度、产量的数量关系,列方程组
解这个方程组,得
答:过长方形土地的长边上离
一端120 m处,作这条边的垂线,
把这块土地分成两块长方形土地.
较大一块土地种甲种作物,较小一块土地种乙种作物.
200 m
100 m
D
C
B
A
F
E
x m
y m
100x
100y
新知探究
200 m
100 m
D
C
B
A
F
E
x m
y m
200x
200y
② 种植方案为:甲、乙两种作物的种植区域分别为长方形AFEB和FDCE.此时设 CE=x m ,BE= y m,根据问题中涉及长度、产量的数量关系,列方程组
解这个方程组,得
答:过长方形土地的宽边上离
一端60 m处,作这条边的垂线,
把这块土地分成两块长方形土地.
较大一块土地种甲种作物,较小一块土地种乙种作物.
巩固练习
巩固练习
新知探究
例3 如图,长青化工厂与 A,B 两地有公路、铁路相连.这家工厂从 A 地购买一批每吨 1 000 元的原料运回工厂,制成每吨 8 000 元的产品运到 B 地.已知公路运价为 1.5 元/(t·km),铁路运价为 1.2 元/(t·km),且这两次运输共支出公路运费 15 000 元,铁路运费 97 200 元.这批产品的销售款比原料费与运输费的和多多少元?
新知探究
分析:销售款与产品数量有关,原料费与原料数量有关.
设制成 x t 产品,购买 y t 原料,根据题中数量关系填写表格.
总结:(1)销售款 = 产品数量 × 8 000.
(2)原料费 = 原料数量 × 1 000.
(3)运输费 = 公路运费 + 铁路运费.
产品 x t 原料 y t 合计
公路运费/元 15 000
铁路运费/元 97 200
价值/元 8 000 x 1 000 y
产品 x t 原料 y t 合计
公路运费/元
铁路运费/元
价值/元 8 000 x 1 000 y
1.2×120 y
1.2×110 x
1.5×20 y
1.5×20 x
1.2×110x+1.2×120 y
1.5×20x+1.5×20 y
新知探究
解:设制成 x t 产品,购买 y t 原料.
由题意,列方程组
解这个方程组,得
销售款 = 8 000 x = 8 000 × 300 = 2 400 000(元)
原料费 = 1 000 y = 1 000 × 400 = 400 000(元)
运输费 = 公路运费 + 铁路运费 = 15 000 + 97 200 = 112 200(元)
2 400 000 -(400 000 + 112 200) =1 887 800(元)
答:这批产品的销售款比原料费与运输费的和多1 887 800元.
巩固练习
巩固练习
课堂练习
D
课堂练习
D
课堂练习
课堂练习
课堂练习
课堂练习
课堂练习
归纳小结
列二元一次方程组解应用题
1.基本思想方法:
(1)列方程组解应用题是把“未知”转化成“已知”的过程;它的关键是把未知量与已知量联系起来,找出题目中等量关系列方程组;
归纳小结
列二元一次方程组解应用题
(2)一般情况下,有几个未知量就必须列出几个方程,所列方程必须满足:
①方程两边表示的是同类量;
②同类量的单位要统一;
③方程两边的数值要相等.
归纳小结
列二元一次方程组解应用题
2.列方程组解应用题的一般步骤:
审→设→找→列→解→答.
(1)审:通过审题,把实际问题抽象成数学问题;
(2)设:分析已知量和未知量,并用字母表示其中
的两个未知量(设元);
(3)找:找出能表示题意的两个相等关系;
(4)列:根据相等关系列出方程组;
(5)解:解这个方程组,求出未知数的值;
(6)答:检验所求解是否符合实际意义,写出答案.
8.3实际问题与二元一次方程组
谢谢观看
二元一次方程组
第八章
二元一次方程组
8.3实际问题与二元一次方程组
教学目标/Teaching aims
1
能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列出二元一次方程组并求解。
2
熟练运用消元法解简单的二元一次方程组。
复习回顾
思考:
列方程解应用题常用的几种数量关系:
(1)行程问题:
路程=速度×时间
顺水(风)速度=静水(风)速度+水(风)流速度
(2)工程问题:
工作量=工作效率×工作时间
复习回顾
(3)利息问题:
年利率=年利息÷本金×100%;
本息和=本金+利息;
总利润=每件商品的利润×销量.
(4)利润问题:
商品利润 = 商品售价 - 商品进价;
商品售价 = 标价×折扣数;
(商品利润=商品进价×商品利润率)
复习回顾
圆面积=πr2;
(5)面积问题:
矩形面积=长×宽;
平行四边形面积=底×高;
正方形面积=边长2;
三角形面积=底乘以高的一半;
新知探究
例1.养牛场原有30只母牛和15只小牛,1天约需用饲675kg;一周后又购进12只母牛和5只小牛,这时1天约需用饲料940kg.饲养员李大叔估计平均每只母牛1天约需饲料18~20kg,每只小牛1天约需饲料7~8kg.你能否通过计算检验他的估计?
1、怎样检验他的估计呢?
2、题目中包含怎样的等量关系?
新知探究
等量关系
设平均每只母牛1天需饲料x千克,小牛需y千克,则
30只母牛和15只小牛1天需饲料为(30x+15y)千克,
42只母牛和20只小牛1天需饲料为(42x+20y)千克.
解:设平均每只母牛1天需饲料x千克,小牛需y千克,依题意得
∴平均每只母牛1天需饲料20千克,小牛需5千克.
饲养员大叔对母牛的食量估计较准,对小牛的食量估计偏高.
巩固练习
巩固练习
新知探究
例2 据统计资料,甲、乙两种作物的单位面积产量的比 1:2. 现要把一块长 200 m ,宽 100 m 的长方形土地,分为两块小长方形土地,分别种植这两种作物. 怎样划分这块土地,使甲、乙两种作物的总产量的比是 3:4 ?
200 m
100 m
总产量 = 单位面积产量×面积
新知探究
① 种植方案为:甲、乙两种作物的种植区域分别为长方形AEFD和BCFE.此时设 AE=x m ,BE= y m,根据问题中涉及长度、产量的数量关系,列方程组
解这个方程组,得
答:过长方形土地的长边上离
一端120 m处,作这条边的垂线,
把这块土地分成两块长方形土地.
较大一块土地种甲种作物,较小一块土地种乙种作物.
200 m
100 m
D
C
B
A
F
E
x m
y m
100x
100y
新知探究
200 m
100 m
D
C
B
A
F
E
x m
y m
200x
200y
② 种植方案为:甲、乙两种作物的种植区域分别为长方形AFEB和FDCE.此时设 CE=x m ,BE= y m,根据问题中涉及长度、产量的数量关系,列方程组
解这个方程组,得
答:过长方形土地的宽边上离
一端60 m处,作这条边的垂线,
把这块土地分成两块长方形土地.
较大一块土地种甲种作物,较小一块土地种乙种作物.
巩固练习
巩固练习
新知探究
例3 如图,长青化工厂与 A,B 两地有公路、铁路相连.这家工厂从 A 地购买一批每吨 1 000 元的原料运回工厂,制成每吨 8 000 元的产品运到 B 地.已知公路运价为 1.5 元/(t·km),铁路运价为 1.2 元/(t·km),且这两次运输共支出公路运费 15 000 元,铁路运费 97 200 元.这批产品的销售款比原料费与运输费的和多多少元?
新知探究
分析:销售款与产品数量有关,原料费与原料数量有关.
设制成 x t 产品,购买 y t 原料,根据题中数量关系填写表格.
总结:(1)销售款 = 产品数量 × 8 000.
(2)原料费 = 原料数量 × 1 000.
(3)运输费 = 公路运费 + 铁路运费.
产品 x t 原料 y t 合计
公路运费/元 15 000
铁路运费/元 97 200
价值/元 8 000 x 1 000 y
产品 x t 原料 y t 合计
公路运费/元
铁路运费/元
价值/元 8 000 x 1 000 y
1.2×120 y
1.2×110 x
1.5×20 y
1.5×20 x
1.2×110x+1.2×120 y
1.5×20x+1.5×20 y
新知探究
解:设制成 x t 产品,购买 y t 原料.
由题意,列方程组
解这个方程组,得
销售款 = 8 000 x = 8 000 × 300 = 2 400 000(元)
原料费 = 1 000 y = 1 000 × 400 = 400 000(元)
运输费 = 公路运费 + 铁路运费 = 15 000 + 97 200 = 112 200(元)
2 400 000 -(400 000 + 112 200) =1 887 800(元)
答:这批产品的销售款比原料费与运输费的和多1 887 800元.
巩固练习
巩固练习
课堂练习
D
课堂练习
D
课堂练习
课堂练习
课堂练习
课堂练习
课堂练习
归纳小结
列二元一次方程组解应用题
1.基本思想方法:
(1)列方程组解应用题是把“未知”转化成“已知”的过程;它的关键是把未知量与已知量联系起来,找出题目中等量关系列方程组;
归纳小结
列二元一次方程组解应用题
(2)一般情况下,有几个未知量就必须列出几个方程,所列方程必须满足:
①方程两边表示的是同类量;
②同类量的单位要统一;
③方程两边的数值要相等.
归纳小结
列二元一次方程组解应用题
2.列方程组解应用题的一般步骤:
审→设→找→列→解→答.
(1)审:通过审题,把实际问题抽象成数学问题;
(2)设:分析已知量和未知量,并用字母表示其中
的两个未知量(设元);
(3)找:找出能表示题意的两个相等关系;
(4)列:根据相等关系列出方程组;
(5)解:解这个方程组,求出未知数的值;
(6)答:检验所求解是否符合实际意义,写出答案.
8.3实际问题与二元一次方程组
谢谢观看
二元一次方程组
