7.2.2 用坐标表示平移 课时2 课件(33张ppt)
文档属性
| 名称 | 7.2.2 用坐标表示平移 课时2 课件(33张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 813.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 00:00:00 | ||
图片预览







文档简介
(共33张PPT)
第七章 平面直角坐标系
人教版七年级 下册
主讲:XXX
7.2.2 用坐标表示平移
(课时2)
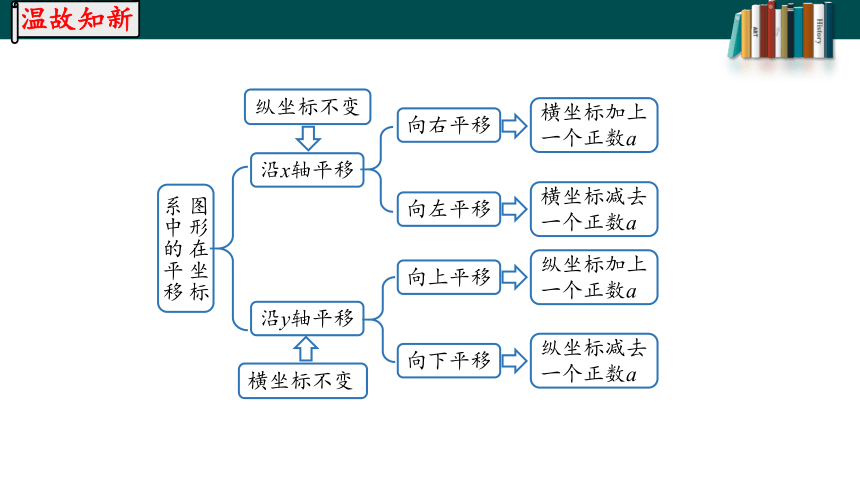
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
横坐标不变
向右平移
向左平移
向上平移
向下平移
横坐标加上一个正数a
横坐标减去一个正数a
纵坐标加上一个正数a
纵坐标减去一个正数a
温故知新
1. 掌握点的坐标的变化引起的平面直角坐标系中点或图形平移的规律.
2. 进一步体会平面直角坐标系是数与形之间的桥梁,感受代数与几何的相互转化,初步建立空间概念.
素养目标
上一节课我们学习了图形的平移引起的图形上点的坐标的变化规律,反过来,这节课我们将探讨图形上点的坐标的某种变化引起的图形平移.
课堂导入
如图,已知点 A 的坐标是(2,3),把它的横坐标加 5,纵坐标不变,得到点 A1,点 A1 的坐标是什么?
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
点A所在位置发生了什么变化?
A
A1 (3,-3)
A1
点 A 向右平移了 5 个单位长度.
知识点:由坐标变化确定平移方式
新知探究
如图,已知点 A 的坐标是(2,3),把它的纵坐标加 4,横坐标不变,得到点 A2,点 A2 的坐标是什么?
点A所在位置发生了什么变化?
A2 (-2,1)
点 A 向上平移了 4 个单位长度.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
A2
知识点:由坐标变化确定平移方式
新知探究
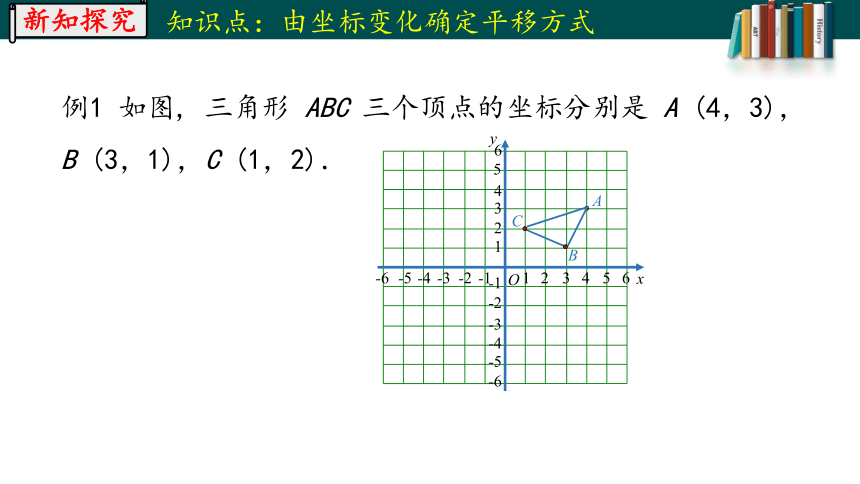
例1 如图, 三角形 ABC 三个顶点的坐标分别是 A (4,3),
B (3,1),C (1,2).
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
知识点:由坐标变化确定平移方式
新知探究
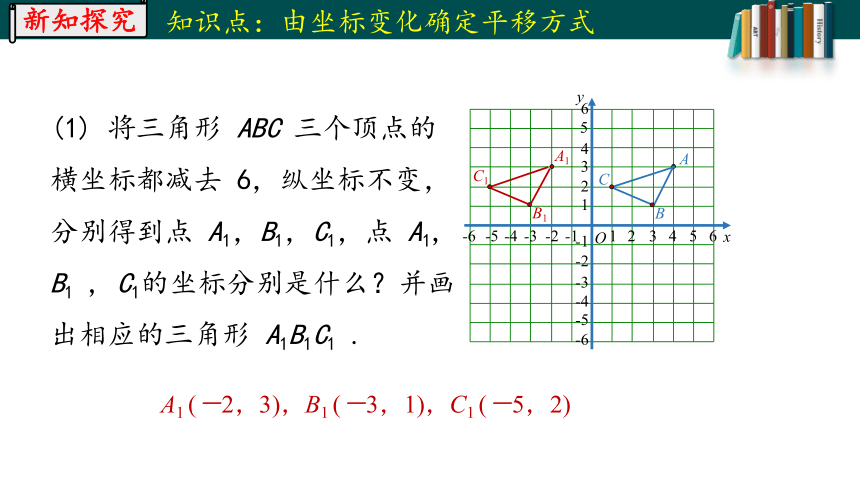
(1) 将三角形 ABC 三个顶点的横坐标都减去 6,纵坐标不变,分别得到点 A1,B1,C1,点 A1, B1 , C1的坐标分别是什么?并画出相应的三角形 A1B1C1 .
A1 (-2,3),B1 (-3,1),C1 (-5,2)
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
知识点:由坐标变化确定平移方式
新知探究
(2) 三角形 A1B1C1 与三角形 ABC 的大小、形状和位置有什么关系?
三角形 ABC 向左平移了 6 个单位长度得到三角形A1B1C1 ,因此所得三角形 A1B1C1 与三角形 ABC 的大小、形状完全相同.
知识点:由坐标变化确定平移方式
新知探究
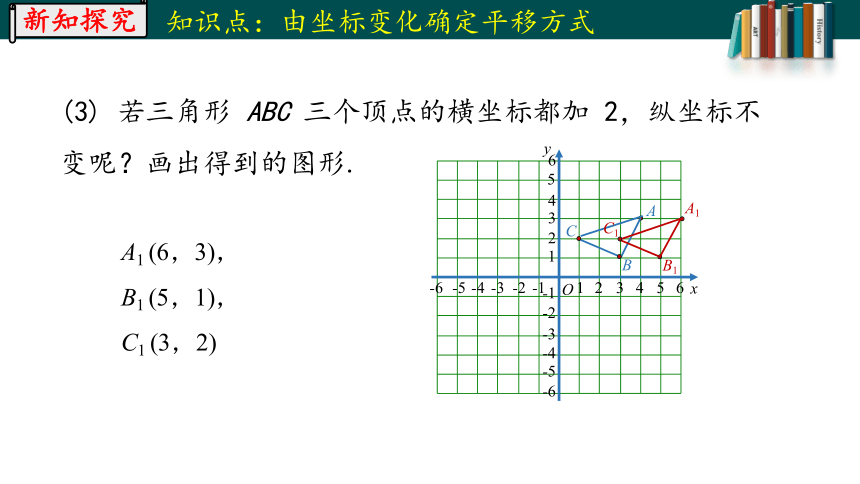
(3) 若三角形 ABC 三个顶点的横坐标都加 2,纵坐标不变呢?画出得到的图形.
A1 (6,3),
B1 (5,1),
C1 (3,2)
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
知识点:由坐标变化确定平移方式
新知探究
在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数 a,相应的新图形就是把原图形向右(或向左)平移 a 个单位长度.
知识点:由坐标变化确定平移方式
新知探究
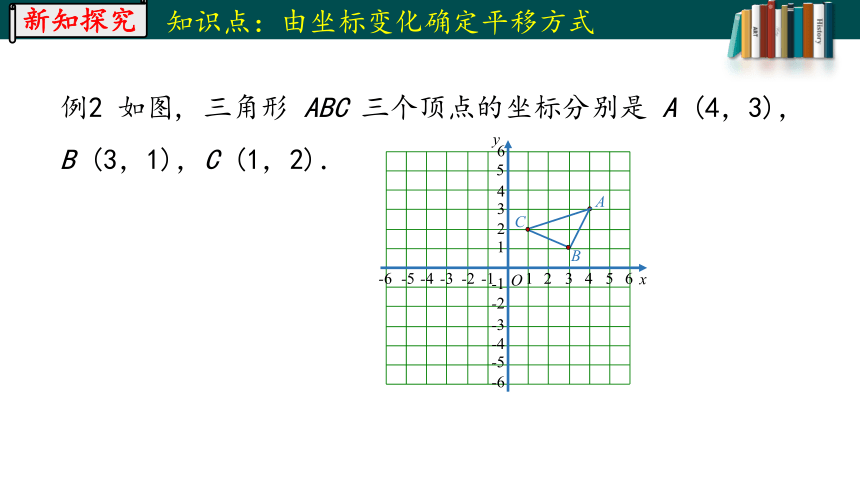
例2 如图, 三角形 ABC 三个顶点的坐标分别是 A (4,3),
B (3,1),C (1,2).
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
知识点:由坐标变化确定平移方式
新知探究
(1) 将三角形 ABC 三个顶点的纵坐标都减去 5,横坐标不变,分别得到点 A2,B2,C2,点 A2,B2 ,C2 坐标分别是什么?并画出相应的三角形 A2B2C2 .
A2 (4,-2),B2 (3,-4),C2 (1,-3)
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A2
B2
C2
知识点:由坐标变化确定平移方式
新知探究
(2) 三角形 A2B2C2 与三角形 ABC 的大小、形状和位置有什么关系?
三角形 ABC 向下平移了 5 个单位长度得到三角形A2B2C2 ,因此所得三角形 A2B2C2 与三角形 ABC 的大小、形状完全相同.
知识点:由坐标变化确定平移方式
新知探究
(3) 若三角形 ABC 三个顶点的纵坐标都加 2,横坐标不变呢?画出得到的图形.
A2 (4,5),B2 (3,3),C2 (1,4)
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A2
B2
C2
知识点:由坐标变化确定平移方式
新知探究
在平面直角坐标系内,如果把一个图形的各个点的纵坐标都加(或减去)一个正数 b,相应的新图形就是把原图形向上(或向下)平移 b 个单位长度.
知识点:由坐标变化确定平移方式
新知探究
思考 如图,将三角形 ABC 三个顶点的横坐标都减去 6,同时纵坐标减去 5,能得到什么结论?画出得到的图形.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
A2
B2
C2
知识点:由坐标变化确定平移方式
新知探究
所得三角形可以由三角形 ABC 向左平移 6 个单位长度,再向下平移 5 个单位长度得到.两个三角形的大小、形状完全相同.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
A2
B2
C2
知识点:由坐标变化确定平移方式
新知探究
一个图形依次沿 x 轴方向、y 轴方向平移后所得图形上的点与原来图形对应点 (x,y) 的坐标之间的关系:
对应点 的坐标 平移方向和平移距离
(x+a , y+b)
(x+a , yb)
(xa , y+b)
(xa , yb)
向右平移 a 个单位长度,向上平移 b 个单位长度
向右平移 a 个单位长度,向下平移 b 个单位长度
向左平移 a 个单位长度,向上平移 b 个单位长度
向左平移 a 个单位长度,向下平移 b 个单位长度
知识点:由坐标变化确定平移方式
新知探究
跟踪练习
1.点 N (1,3)可以看作由点 M (1,1)( )
A. 向上平移 4 个单位长度得到的
B. 向左平移 4 个单位长度得到的
C. 向下平移 4 个单位长度得到的
D. 向右平移 4 个单位长度得到的
A
2. 在平面直角坐标系中,三角形 ABC 的三个顶点的横坐标保持不变,纵坐标都减去 3,则得到的新三角形与原三角形相比,向( ) 平移了 3 个单位长度.
A. 左 B. 右
C. 下 D. 上
C
3. 如图,与图 1 中的三角形相比,图 2 中的三角形发生的位置变化是( )
A. 向左平移 3 个单位长度
B. 向左平移 1 个单位长度
C. 向上平移 3 个单位长度
D. 向下平移 1 个单位长度
A
由点的坐标变化确定点的平移方式的方法
1. 平移后的点与平移前的点的横坐标的差反映了点沿 x 轴平移的情况,若差值为正,则表示向右平移,若差值为负,则表示向左平移.
2. 平移后的点与平移前的点的纵坐标的差反映了点沿 y 轴平移的情况,若差值为正,则表示向上平移,若差值为负,则表示向下平移.
知识点:由坐标变化确定平移方式
新知探究
图形在坐标系中的平移
横坐标加上一个正数a
向右平移
横坐标减去一个正数a
向左平移
纵坐标加上一个正数a
向上平移
纵坐标减去一个正数a
向下平移
课堂小结
当堂检测
基础练习:
1.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点 A,B 的坐标分别为( 1,0),(0,).现将该三角板向右平移使点 A 与点 O 重合,得到三角形 OCB', 则点 B 的对应点 B' 的坐标是( )
A.(1,0) B. (,)
C.(1,) D.(1,)
C
2. 已知点 A,B 的坐标分别为 (2,0),(0,1),将线段 AB 平移至 A1B1 ,若点 A1,B1 的坐标分别为 (3,b),(a,2),则 a+b 的值为 ( )
A. 2 B. 3 C. 4 D. 5
A
3.如图,点A,B的坐标分别为(1,2),(4,0),将三角形AOB沿x轴向右平移,得到三角形CDE,已知DB=1,则点C的坐标为 ( )
A.(2,2) B.(4,3) C.(3,2) D.(4,2)
D
能力提升:
4. 如图,在平面直角坐标系中,已知点 A (3,3),B (5,1),C (2,0),P (a,b) 是三角形 ABC 的边 AC 上任意一点,三角形 ABC 经过平移后得到三角形 A1B1C1,点 P 的对应点为 P1 (a6,b2).
(1) 写出点 A1,B1,C1 的坐标.
解:(1) ∵ 点 P (a,b)的对应点为 P1 (a6,b2),
∴ 平移规律为向右平移 6 个单位长度,向下平移 2 个单位长度.
∴ A(3,3),B(5,1),C(2,0)的对应点的坐标分别为 A1(3,1),B1(1,1),C1(4,2).
A1
C1
B1
解:三角形 A1B1C1 如图所示.
(2) 在图中画出三角形 A1B1C1.
解:如图,借助网格可知三角形 AOA1 的面积为
.
(3) 连接 OA,OA1,AA1,求三角形 AOA1 的面积.
A1
C1
B1
拓展延伸:
5. 如图,已知三角形ABC,其中点A和点B的坐标分别为(2,-4)和(-2,2).
(1)请在图中建立适当的平面直角坐标系;
(2)点C的坐标为 ;
(3)若点D是y轴上的一点,连接BD,DC,满足S三角形ABC=S三角形DBC,
则点D的坐标为 ,S三角形DBC= ;
(4)已知点P(3,n+2),Q(6,n)均是第一象限内的点,连接PQ,
平移线段PQ使点P,Q分别落在两条坐标轴上.求点P平移后的对应点的坐标.
5. 解:(1)由题意,建立如图所示的平面直角坐标系.
(2)(3,2)
(3)(0,-4)或(0,8) 15
设点D到BC的距离为h,∵S三角形ABC=S三角形DBC=×5×6=×5h=15,
∴h=6,
∴点D的坐标为(0,-4)或(0,8).
(4)设平移后点P,Q的对应点分别是点P',Q'.
分两种情况:
①若点P'在y轴上,点Q'在x轴上,
则点P'的横坐标为0,点Q'的纵坐标为0,
∴线段PQ先向左平移3个单位长度,再向下平移n个单位长度得到线段P'Q',
∴点P平移后的对应点的坐标为(0,2).
②若点P'在x轴上,点Q'在y轴上,
则点P'的纵坐标为0,点Q'的横坐标为0,
∴线段PQ先向左平移6个单位长度,再向下平移(n+2)个单位长度得到线段P'Q',
∴点P平移后的对应点的坐标为(-3,0).
综上所述,点P平移后的对应点的坐标为(0,2)或(-3,0).
谢谢!再见!
主讲:XXX
第七章 平面直角坐标系
人教版七年级 下册
主讲:XXX
7.2.2 用坐标表示平移
(课时2)
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
横坐标不变
向右平移
向左平移
向上平移
向下平移
横坐标加上一个正数a
横坐标减去一个正数a
纵坐标加上一个正数a
纵坐标减去一个正数a
温故知新
1. 掌握点的坐标的变化引起的平面直角坐标系中点或图形平移的规律.
2. 进一步体会平面直角坐标系是数与形之间的桥梁,感受代数与几何的相互转化,初步建立空间概念.
素养目标
上一节课我们学习了图形的平移引起的图形上点的坐标的变化规律,反过来,这节课我们将探讨图形上点的坐标的某种变化引起的图形平移.
课堂导入
如图,已知点 A 的坐标是(2,3),把它的横坐标加 5,纵坐标不变,得到点 A1,点 A1 的坐标是什么?
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
点A所在位置发生了什么变化?
A
A1 (3,-3)
A1
点 A 向右平移了 5 个单位长度.
知识点:由坐标变化确定平移方式
新知探究
如图,已知点 A 的坐标是(2,3),把它的纵坐标加 4,横坐标不变,得到点 A2,点 A2 的坐标是什么?
点A所在位置发生了什么变化?
A2 (-2,1)
点 A 向上平移了 4 个单位长度.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
A2
知识点:由坐标变化确定平移方式
新知探究
例1 如图, 三角形 ABC 三个顶点的坐标分别是 A (4,3),
B (3,1),C (1,2).
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
知识点:由坐标变化确定平移方式
新知探究
(1) 将三角形 ABC 三个顶点的横坐标都减去 6,纵坐标不变,分别得到点 A1,B1,C1,点 A1, B1 , C1的坐标分别是什么?并画出相应的三角形 A1B1C1 .
A1 (-2,3),B1 (-3,1),C1 (-5,2)
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
知识点:由坐标变化确定平移方式
新知探究
(2) 三角形 A1B1C1 与三角形 ABC 的大小、形状和位置有什么关系?
三角形 ABC 向左平移了 6 个单位长度得到三角形A1B1C1 ,因此所得三角形 A1B1C1 与三角形 ABC 的大小、形状完全相同.
知识点:由坐标变化确定平移方式
新知探究
(3) 若三角形 ABC 三个顶点的横坐标都加 2,纵坐标不变呢?画出得到的图形.
A1 (6,3),
B1 (5,1),
C1 (3,2)
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
知识点:由坐标变化确定平移方式
新知探究
在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数 a,相应的新图形就是把原图形向右(或向左)平移 a 个单位长度.
知识点:由坐标变化确定平移方式
新知探究
例2 如图, 三角形 ABC 三个顶点的坐标分别是 A (4,3),
B (3,1),C (1,2).
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
知识点:由坐标变化确定平移方式
新知探究
(1) 将三角形 ABC 三个顶点的纵坐标都减去 5,横坐标不变,分别得到点 A2,B2,C2,点 A2,B2 ,C2 坐标分别是什么?并画出相应的三角形 A2B2C2 .
A2 (4,-2),B2 (3,-4),C2 (1,-3)
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A2
B2
C2
知识点:由坐标变化确定平移方式
新知探究
(2) 三角形 A2B2C2 与三角形 ABC 的大小、形状和位置有什么关系?
三角形 ABC 向下平移了 5 个单位长度得到三角形A2B2C2 ,因此所得三角形 A2B2C2 与三角形 ABC 的大小、形状完全相同.
知识点:由坐标变化确定平移方式
新知探究
(3) 若三角形 ABC 三个顶点的纵坐标都加 2,横坐标不变呢?画出得到的图形.
A2 (4,5),B2 (3,3),C2 (1,4)
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A2
B2
C2
知识点:由坐标变化确定平移方式
新知探究
在平面直角坐标系内,如果把一个图形的各个点的纵坐标都加(或减去)一个正数 b,相应的新图形就是把原图形向上(或向下)平移 b 个单位长度.
知识点:由坐标变化确定平移方式
新知探究
思考 如图,将三角形 ABC 三个顶点的横坐标都减去 6,同时纵坐标减去 5,能得到什么结论?画出得到的图形.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
A2
B2
C2
知识点:由坐标变化确定平移方式
新知探究
所得三角形可以由三角形 ABC 向左平移 6 个单位长度,再向下平移 5 个单位长度得到.两个三角形的大小、形状完全相同.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
y
x
A
C
B
A1
B1
C1
A2
B2
C2
知识点:由坐标变化确定平移方式
新知探究
一个图形依次沿 x 轴方向、y 轴方向平移后所得图形上的点与原来图形对应点 (x,y) 的坐标之间的关系:
对应点 的坐标 平移方向和平移距离
(x+a , y+b)
(x+a , yb)
(xa , y+b)
(xa , yb)
向右平移 a 个单位长度,向上平移 b 个单位长度
向右平移 a 个单位长度,向下平移 b 个单位长度
向左平移 a 个单位长度,向上平移 b 个单位长度
向左平移 a 个单位长度,向下平移 b 个单位长度
知识点:由坐标变化确定平移方式
新知探究
跟踪练习
1.点 N (1,3)可以看作由点 M (1,1)( )
A. 向上平移 4 个单位长度得到的
B. 向左平移 4 个单位长度得到的
C. 向下平移 4 个单位长度得到的
D. 向右平移 4 个单位长度得到的
A
2. 在平面直角坐标系中,三角形 ABC 的三个顶点的横坐标保持不变,纵坐标都减去 3,则得到的新三角形与原三角形相比,向( ) 平移了 3 个单位长度.
A. 左 B. 右
C. 下 D. 上
C
3. 如图,与图 1 中的三角形相比,图 2 中的三角形发生的位置变化是( )
A. 向左平移 3 个单位长度
B. 向左平移 1 个单位长度
C. 向上平移 3 个单位长度
D. 向下平移 1 个单位长度
A
由点的坐标变化确定点的平移方式的方法
1. 平移后的点与平移前的点的横坐标的差反映了点沿 x 轴平移的情况,若差值为正,则表示向右平移,若差值为负,则表示向左平移.
2. 平移后的点与平移前的点的纵坐标的差反映了点沿 y 轴平移的情况,若差值为正,则表示向上平移,若差值为负,则表示向下平移.
知识点:由坐标变化确定平移方式
新知探究
图形在坐标系中的平移
横坐标加上一个正数a
向右平移
横坐标减去一个正数a
向左平移
纵坐标加上一个正数a
向上平移
纵坐标减去一个正数a
向下平移
课堂小结
当堂检测
基础练习:
1.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点 A,B 的坐标分别为( 1,0),(0,).现将该三角板向右平移使点 A 与点 O 重合,得到三角形 OCB', 则点 B 的对应点 B' 的坐标是( )
A.(1,0) B. (,)
C.(1,) D.(1,)
C
2. 已知点 A,B 的坐标分别为 (2,0),(0,1),将线段 AB 平移至 A1B1 ,若点 A1,B1 的坐标分别为 (3,b),(a,2),则 a+b 的值为 ( )
A. 2 B. 3 C. 4 D. 5
A
3.如图,点A,B的坐标分别为(1,2),(4,0),将三角形AOB沿x轴向右平移,得到三角形CDE,已知DB=1,则点C的坐标为 ( )
A.(2,2) B.(4,3) C.(3,2) D.(4,2)
D
能力提升:
4. 如图,在平面直角坐标系中,已知点 A (3,3),B (5,1),C (2,0),P (a,b) 是三角形 ABC 的边 AC 上任意一点,三角形 ABC 经过平移后得到三角形 A1B1C1,点 P 的对应点为 P1 (a6,b2).
(1) 写出点 A1,B1,C1 的坐标.
解:(1) ∵ 点 P (a,b)的对应点为 P1 (a6,b2),
∴ 平移规律为向右平移 6 个单位长度,向下平移 2 个单位长度.
∴ A(3,3),B(5,1),C(2,0)的对应点的坐标分别为 A1(3,1),B1(1,1),C1(4,2).
A1
C1
B1
解:三角形 A1B1C1 如图所示.
(2) 在图中画出三角形 A1B1C1.
解:如图,借助网格可知三角形 AOA1 的面积为
.
(3) 连接 OA,OA1,AA1,求三角形 AOA1 的面积.
A1
C1
B1
拓展延伸:
5. 如图,已知三角形ABC,其中点A和点B的坐标分别为(2,-4)和(-2,2).
(1)请在图中建立适当的平面直角坐标系;
(2)点C的坐标为 ;
(3)若点D是y轴上的一点,连接BD,DC,满足S三角形ABC=S三角形DBC,
则点D的坐标为 ,S三角形DBC= ;
(4)已知点P(3,n+2),Q(6,n)均是第一象限内的点,连接PQ,
平移线段PQ使点P,Q分别落在两条坐标轴上.求点P平移后的对应点的坐标.
5. 解:(1)由题意,建立如图所示的平面直角坐标系.
(2)(3,2)
(3)(0,-4)或(0,8) 15
设点D到BC的距离为h,∵S三角形ABC=S三角形DBC=×5×6=×5h=15,
∴h=6,
∴点D的坐标为(0,-4)或(0,8).
(4)设平移后点P,Q的对应点分别是点P',Q'.
分两种情况:
①若点P'在y轴上,点Q'在x轴上,
则点P'的横坐标为0,点Q'的纵坐标为0,
∴线段PQ先向左平移3个单位长度,再向下平移n个单位长度得到线段P'Q',
∴点P平移后的对应点的坐标为(0,2).
②若点P'在x轴上,点Q'在y轴上,
则点P'的纵坐标为0,点Q'的横坐标为0,
∴线段PQ先向左平移6个单位长度,再向下平移(n+2)个单位长度得到线段P'Q',
∴点P平移后的对应点的坐标为(-3,0).
综上所述,点P平移后的对应点的坐标为(0,2)或(-3,0).
谢谢!再见!
主讲:XXX
