6.1.1算数平方根 课件(共25张PPT)
文档属性
| 名称 | 6.1.1算数平方根 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 786.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 15:39:33 | ||
图片预览






文档简介
(共25张PPT)
第六章 实数
人教版七年级 下册
主讲:XXX
6.1.1 算术平方根
1.了解算术平方根的概念,会用根号表示一个数的算术平方根.
2.会求非负数的算术平方根,掌握算术平方根的非负性.
素养目标
学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm2 的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
正方形画布的边长应取 5 dm.
课堂导入
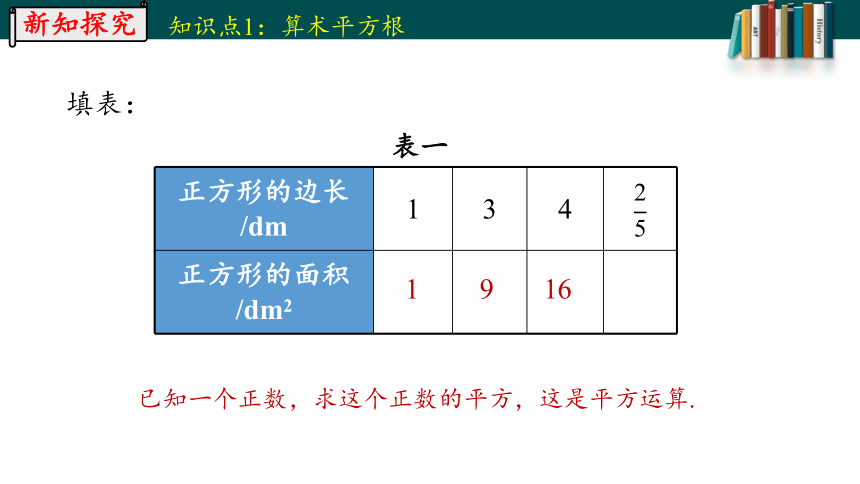
已知一个正数,求这个正数的平方,这是平方运算.
正方形的边长/dm 1 3 4
正方形的面积/dm2
1
填表:
9
16
表一
知识点1:算术平方根
新知探究
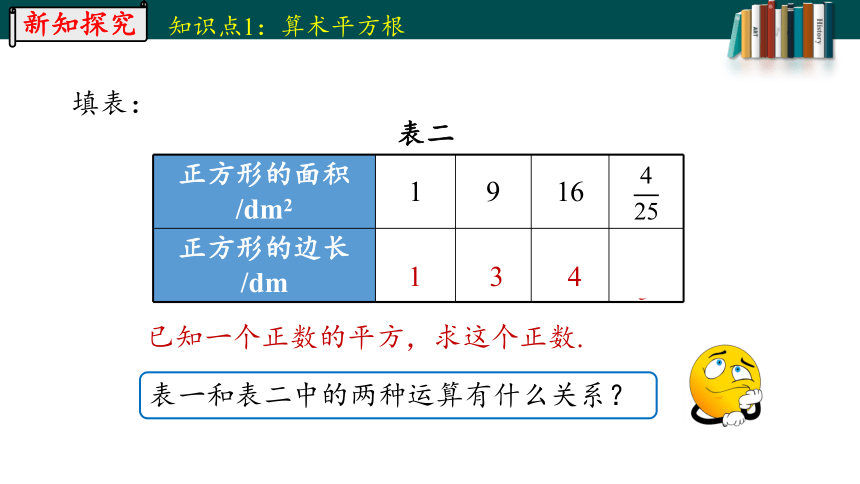
正方形的面积/dm2 1 9 16
正方形的边长/dm
1
填表:
3
4
已知一个正数的平方,求这个正数.
表二
表一和表二中的两种运算有什么关系?
知识点1:算术平方根
新知探究
一般地,如果一个正数 x 的平方等于 a,即 x2=a,那么这个正数 x 叫做 a 的算术平方根.
规定:0 的算术平方根是 0.
算术平方根是它本身的数只有 0 和 1.
知识点1:算术平方根
新知探究
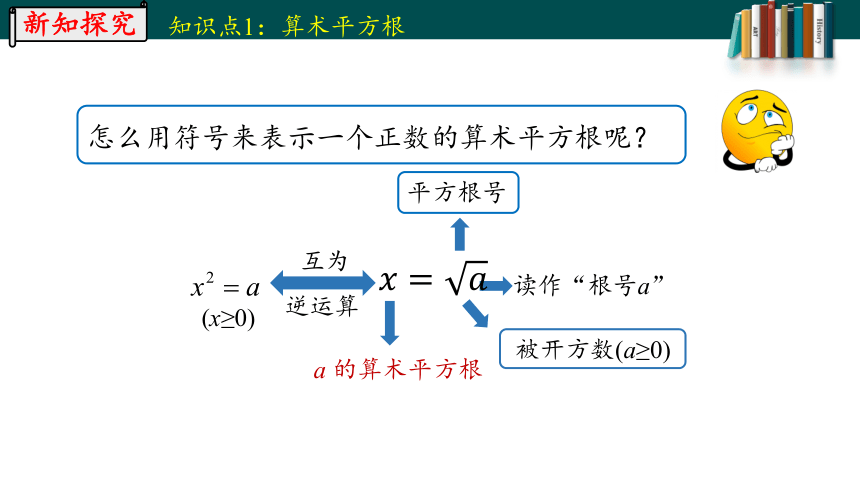
a 的算术平方根
互为
逆运算
平方根号
被开方数(a≥0)
读作“根号a”
(x≥0)
怎么用符号来表示一个正数的算术平方根呢?
知识点1:算术平方根
新知探究
例1 分别求下列各数的算术平方根:
(1) 100; (2) ; (3) 0.0001.
解:(1) 由于102=100, 因此 10.
(2)由于 ,因此 .
(3) 由于 0.012=0.0001,因此 .
被开方数越大,对应的算术平方根也越大.
知识点1:算术平方根
新知探究
1.一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
2.0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根
一个正数的算术平方根有1个
合作与交流:
知识点2:算术平方根的性质
新知探究
(1)49的算术平方根是______;
7
2
一步运算
两步运算
(2) 的算术平方根是______.
例2 填空:
注意文字或算术的表述,读清题意,再进行计算,以防误解.
归纳:
知识点2:算术平方根的性质
新知探究
问题1: (1)因为_____2=64,所以64的算术平方根是____,
即 =______.
(2)因为_____2=0.25,所以0.25的算术平方根是______,
即 =______.
(3)因为_____2=0,所以0的算术平方根是______,
即 =______.
8
8
8
0.5
0.5
0.5
0
0
0
问题2: 讨论:在 中,被开方数a是一_____数,
算术平方根 是一个______数.
非负
非负
知识点2:算术平方根的性质
新知探究
是什么数?其中a可以取任何数吗?
算术平方根的双重非负性
a 的算术平方根
非负数0
非负数a≥0
知识点2:算术平方根的性质
新知探究
到目前为止,表示非负数的式子有:
|a| ≥ 0;a2 ≥ 0;当a ≥ 0 时, ≥ 0.
知识点2:算术平方根的性质
新知探究
解: 因为 |m-2| ≥0, ≥0,
且 |m-2| + =0,
所以 |m-2| =0, =0,
所以 m=2,n=-2,
所以 m+n=2+(-2)=0.
例3 若 |m-2| + =0,求 m+n 的值.
知识点2:算术平方根的性质
新知探究
几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
归纳
1.(2021 湖州中考)化简的正确结果是( )
A.4 B.±4
C. D.±
C
跟踪练习
2.已知 a,b,c 为有理数,若|a-1| + +(c+4)2=0,则 (a+b+c)2020 = .
1
3.求下列各数的算术平方根.
(1) 144;
(2) 0.0036;
(3) ;
(4) ;
(5) 0.
12.
求一个带分数的算术平方根时,要先把带分数化成假分数.
4.若
解:因为,
所以,
解得,
所以 .
一般地,如果一个正数 x 的平方等于 a,即 x2=a,那么这个正数 x 叫做 a 的算术平方根.
算术平方根
概念
应用
a ≥0
几个非负数的和为0,则每个数均为0.
双重非负性
课堂小结
A
A
当堂检测
基础练习:
B
4.填空:
(1) 一个数的算术平方根是8,则这个数是 .
(2) 一个自然数的算术平方根为a,则这个自然数是___;和这个自然数相邻的下一个自然数是 .
5.计算:
(1) 的算术平方根为 .
(2) 2的算术平方根为____.
3
64
a2
a2+1
3
6.求下列各数的算术平方根:
(1)121; (2) ; (3) 0.0001.
解:(1)因为112 =121,所以121的算术平方根是11,
即 ;
(2)因为 ,所以 的算术平方根是 ,
即
(3)因为0.012 =0.0001,所以0.0001的算术平方根是0.01, 即
能力提升:
8.已知:|x+2y|+ .
求x-3y+4z的值.
解:由题意得:
解得
拓展延伸:
谢谢!再见!
主讲:XXX
第六章 实数
人教版七年级 下册
主讲:XXX
6.1.1 算术平方根
1.了解算术平方根的概念,会用根号表示一个数的算术平方根.
2.会求非负数的算术平方根,掌握算术平方根的非负性.
素养目标
学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm2 的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
正方形画布的边长应取 5 dm.
课堂导入
已知一个正数,求这个正数的平方,这是平方运算.
正方形的边长/dm 1 3 4
正方形的面积/dm2
1
填表:
9
16
表一
知识点1:算术平方根
新知探究
正方形的面积/dm2 1 9 16
正方形的边长/dm
1
填表:
3
4
已知一个正数的平方,求这个正数.
表二
表一和表二中的两种运算有什么关系?
知识点1:算术平方根
新知探究
一般地,如果一个正数 x 的平方等于 a,即 x2=a,那么这个正数 x 叫做 a 的算术平方根.
规定:0 的算术平方根是 0.
算术平方根是它本身的数只有 0 和 1.
知识点1:算术平方根
新知探究
a 的算术平方根
互为
逆运算
平方根号
被开方数(a≥0)
读作“根号a”
(x≥0)
怎么用符号来表示一个正数的算术平方根呢?
知识点1:算术平方根
新知探究
例1 分别求下列各数的算术平方根:
(1) 100; (2) ; (3) 0.0001.
解:(1) 由于102=100, 因此 10.
(2)由于 ,因此 .
(3) 由于 0.012=0.0001,因此 .
被开方数越大,对应的算术平方根也越大.
知识点1:算术平方根
新知探究
1.一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
2.0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根
一个正数的算术平方根有1个
合作与交流:
知识点2:算术平方根的性质
新知探究
(1)49的算术平方根是______;
7
2
一步运算
两步运算
(2) 的算术平方根是______.
例2 填空:
注意文字或算术的表述,读清题意,再进行计算,以防误解.
归纳:
知识点2:算术平方根的性质
新知探究
问题1: (1)因为_____2=64,所以64的算术平方根是____,
即 =______.
(2)因为_____2=0.25,所以0.25的算术平方根是______,
即 =______.
(3)因为_____2=0,所以0的算术平方根是______,
即 =______.
8
8
8
0.5
0.5
0.5
0
0
0
问题2: 讨论:在 中,被开方数a是一_____数,
算术平方根 是一个______数.
非负
非负
知识点2:算术平方根的性质
新知探究
是什么数?其中a可以取任何数吗?
算术平方根的双重非负性
a 的算术平方根
非负数0
非负数a≥0
知识点2:算术平方根的性质
新知探究
到目前为止,表示非负数的式子有:
|a| ≥ 0;a2 ≥ 0;当a ≥ 0 时, ≥ 0.
知识点2:算术平方根的性质
新知探究
解: 因为 |m-2| ≥0, ≥0,
且 |m-2| + =0,
所以 |m-2| =0, =0,
所以 m=2,n=-2,
所以 m+n=2+(-2)=0.
例3 若 |m-2| + =0,求 m+n 的值.
知识点2:算术平方根的性质
新知探究
几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
归纳
1.(2021 湖州中考)化简的正确结果是( )
A.4 B.±4
C. D.±
C
跟踪练习
2.已知 a,b,c 为有理数,若|a-1| + +(c+4)2=0,则 (a+b+c)2020 = .
1
3.求下列各数的算术平方根.
(1) 144;
(2) 0.0036;
(3) ;
(4) ;
(5) 0.
12.
求一个带分数的算术平方根时,要先把带分数化成假分数.
4.若
解:因为,
所以,
解得,
所以 .
一般地,如果一个正数 x 的平方等于 a,即 x2=a,那么这个正数 x 叫做 a 的算术平方根.
算术平方根
概念
应用
a ≥0
几个非负数的和为0,则每个数均为0.
双重非负性
课堂小结
A
A
当堂检测
基础练习:
B
4.填空:
(1) 一个数的算术平方根是8,则这个数是 .
(2) 一个自然数的算术平方根为a,则这个自然数是___;和这个自然数相邻的下一个自然数是 .
5.计算:
(1) 的算术平方根为 .
(2) 2的算术平方根为____.
3
64
a2
a2+1
3
6.求下列各数的算术平方根:
(1)121; (2) ; (3) 0.0001.
解:(1)因为112 =121,所以121的算术平方根是11,
即 ;
(2)因为 ,所以 的算术平方根是 ,
即
(3)因为0.012 =0.0001,所以0.0001的算术平方根是0.01, 即
能力提升:
8.已知:|x+2y|+ .
求x-3y+4z的值.
解:由题意得:
解得
拓展延伸:
谢谢!再见!
主讲:XXX
