人教版七年级下册5.4平移 第1课时 课件(共18张PPT)
文档属性
| 名称 | 人教版七年级下册5.4平移 第1课时 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
第五章 相交线与平行线
5.4 平 移
导入新课
讲授新课
当堂练习
课堂小结
第1课时
学习目标
CONTENTS
01
02
理解平移的概念及决定因素.
会找出平移前后图形中对应点、对应角和对应线段.
掌握平移的性质及其运用.
情景引入
一、平移的相关概念
A
B
C
D
E
F
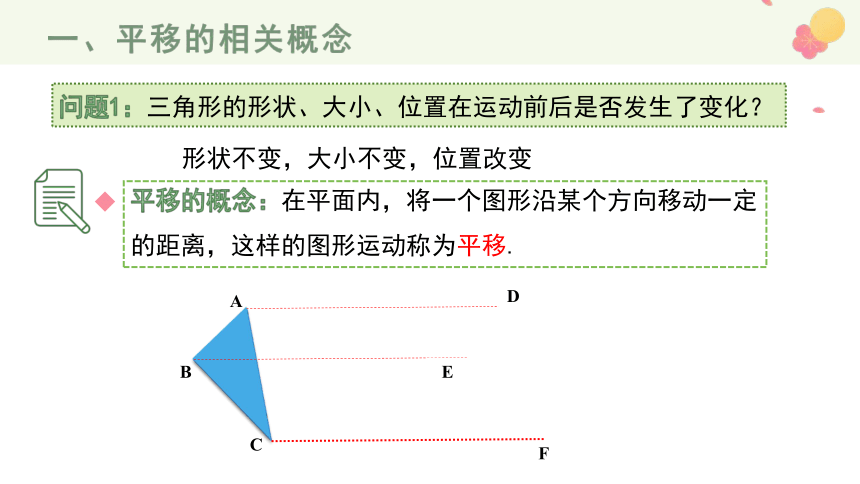
问题1:三角形的形状、大小、位置在运动前后是否发生了变化?
形状不变,大小不变,位置改变
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
一、平移的相关概念
知识点一:平移的相关概念
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
注意
1
平移前后的图形,其形状不变,大小不变,位置改变
典例精析
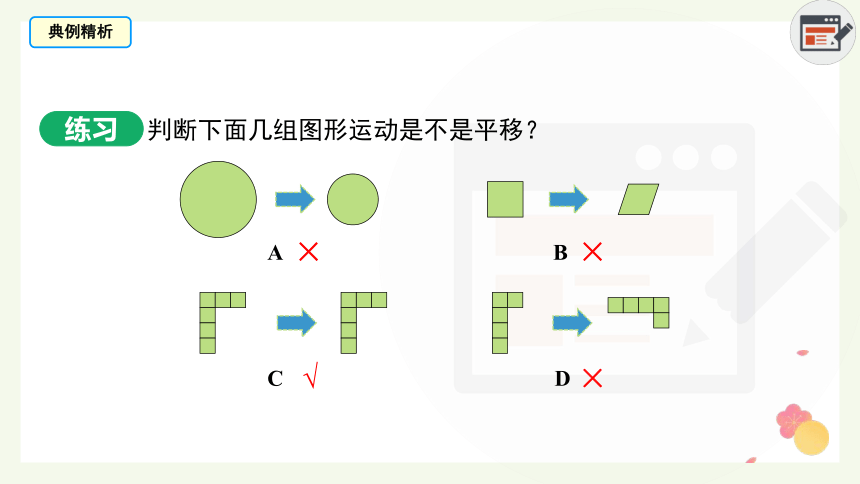
判断下面几组图形运动是不是平移?
A
C
D
B
×
×
√
×
练习
一、平移的相关概念
知识点一:平移的相关概念
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
注意
1
平移前后的图形,其形状不变,大小不变,位置改变
2
图形的平移不一定是水平的,也不一定是竖直的.
图形的平移由移动的方向和距离决定.
3
二、平移的性质
A
B
C
F
I
H
M
D
N
二、平移的性质
A
B
C
F
H
M
1
对应点、对应点连线(方向、距离)
2
对应线段平行(或在同一直线上)
且相等;.
各对应点所连线段平行(或在同一直线上)且相等;
3
小本活页P21
遇到平移,先确定:方向和距离
典例精析
B
A
C
D
E
F
O
1.如图,直角三角形ABC平移得到直角三角形DEF,DE与AC相交于O,若∠B=90°,∠A=60°,BC=8cm.
(1)图中平行的线段有_____________________
(2)∠DEF=________,∠COE=_________,
EF=________cm.
(3)若平移的距离为5cm,则BE=______cm,EC=_________cm;
AB∥DE,AC∥DF
90°
60°
8
5
3
三、平移的画法
如图,平移三角形ABC,使点A移动到点D,画出平移后的三角形DEF
A
B
C
A
B
C
典例精析
如图,平移三角形ABC,使点A移动到点D,画出平移后的三角形DEF
A
B
C
D
E
F
当堂练习
1m
1m
21m
15m
A
C
D
B
图 1
例3:如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
1m
1m
21m
15m
A
C
D
B
图 1
思路点拨:两种平移方式
解:长草部分的面积=(21-1)×(15-1)=280(m2).
当堂练习
1m
21m
15m
A
C
D
B
变式:如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
思路点拨:平移构成规则图形
解:长草部分的面积=(21-1)×15=300(m2).
当堂练习
1. 在平移变换中,平移后的图形与原来的图形________和________都相同,连接各组对应点的线段________且_________.
形状
大小
平行
相等
2. 下列各组图形,可经平移变换由一个图形得到另一个图形的是( )
A
A B C D
当堂练习
3.下列四个图形中,不能通过基本图形平移得到的是( )
A. B.
C. D.
C
当堂练习
4.如图所示,经过平移,四边形 ABCD 的顶点 A 移到点 A′ 处,作出平移后的四边形.
A
B
C
D
A′
课堂小结
(1)平移的基本性质是什么?
(2)回顾探究平移基本性质的过程,你能说出归纳平移基本性质的基本思路吗?
课堂小结
第五章 相交线与平行线
5.4 平 移
导入新课
讲授新课
当堂练习
课堂小结
第1课时
学习目标
CONTENTS
01
02
理解平移的概念及决定因素.
会找出平移前后图形中对应点、对应角和对应线段.
掌握平移的性质及其运用.
情景引入
一、平移的相关概念
A
B
C
D
E
F
问题1:三角形的形状、大小、位置在运动前后是否发生了变化?
形状不变,大小不变,位置改变
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
一、平移的相关概念
知识点一:平移的相关概念
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
注意
1
平移前后的图形,其形状不变,大小不变,位置改变
典例精析
判断下面几组图形运动是不是平移?
A
C
D
B
×
×
√
×
练习
一、平移的相关概念
知识点一:平移的相关概念
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
注意
1
平移前后的图形,其形状不变,大小不变,位置改变
2
图形的平移不一定是水平的,也不一定是竖直的.
图形的平移由移动的方向和距离决定.
3
二、平移的性质
A
B
C
F
I
H
M
D
N
二、平移的性质
A
B
C
F
H
M
1
对应点、对应点连线(方向、距离)
2
对应线段平行(或在同一直线上)
且相等;.
各对应点所连线段平行(或在同一直线上)且相等;
3
小本活页P21
遇到平移,先确定:方向和距离
典例精析
B
A
C
D
E
F
O
1.如图,直角三角形ABC平移得到直角三角形DEF,DE与AC相交于O,若∠B=90°,∠A=60°,BC=8cm.
(1)图中平行的线段有_____________________
(2)∠DEF=________,∠COE=_________,
EF=________cm.
(3)若平移的距离为5cm,则BE=______cm,EC=_________cm;
AB∥DE,AC∥DF
90°
60°
8
5
3
三、平移的画法
如图,平移三角形ABC,使点A移动到点D,画出平移后的三角形DEF
A
B
C
A
B
C
典例精析
如图,平移三角形ABC,使点A移动到点D,画出平移后的三角形DEF
A
B
C
D
E
F
当堂练习
1m
1m
21m
15m
A
C
D
B
图 1
例3:如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
1m
1m
21m
15m
A
C
D
B
图 1
思路点拨:两种平移方式
解:长草部分的面积=(21-1)×(15-1)=280(m2).
当堂练习
1m
21m
15m
A
C
D
B
变式:如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
思路点拨:平移构成规则图形
解:长草部分的面积=(21-1)×15=300(m2).
当堂练习
1. 在平移变换中,平移后的图形与原来的图形________和________都相同,连接各组对应点的线段________且_________.
形状
大小
平行
相等
2. 下列各组图形,可经平移变换由一个图形得到另一个图形的是( )
A
A B C D
当堂练习
3.下列四个图形中,不能通过基本图形平移得到的是( )
A. B.
C. D.
C
当堂练习
4.如图所示,经过平移,四边形 ABCD 的顶点 A 移到点 A′ 处,作出平移后的四边形.
A
B
C
D
A′
课堂小结
(1)平移的基本性质是什么?
(2)回顾探究平移基本性质的过程,你能说出归纳平移基本性质的基本思路吗?
课堂小结
