专题拓展六:乘法公式的拓展应用(含答案)
文档属性
| 名称 | 专题拓展六:乘法公式的拓展应用(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 291.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题拓展六:乘法公式的拓展应用
知识点拨:
乘法公式是初中数学中的重要公式,也是中考常见的考点之一.
平方差公式:(a+b)(a-b)=a2-b2,公式的左边是两个数的和乘这两个数的差,右边正好是这两个数的平方差,两边都有差的运算,关键要准确把握谁减去谁.
完全平方公式:(a+b)2=a2+2ab+b2,(a-b)=a2-2ab+b2,公式的左边是两个数的和(或差)的平方,右边是这两个数的平方和,再加上(或减去)这两个数积的2倍,两边的符号是一致的,要准确把握符号问题.
在解决问题时,要注意观察式子的特点,选择合适的方法和解题思路,不要拘泥于公式的形式,而要深刻理解,加以灵活运用.
完全平方公式的常见变形有:
a2+b2=(a+b)2-2ab=(a-b)2+2ab;
ab=
(a+b)2+(a-b)2 =_______________ .
题型分析
题型一:巧用乘法公式简便计算
1.计算:1002×998-9992 .
题型二:利用乘法公式化简求值
2.先化简,再求值:(2a+1)(2a-1)-(2a-3)2+5,其中a=.
3.先化简,再求值:(2x-y)2-(x-y)(x+y),其中|x+1|+(y-2)2 =0 .
4.先化简,再求值:(2m+n-1)(2m-n+1),其中4m2+2n=4+n2 .
题型三:利用乘法公式求代数式的值
5.已知(2a+b)2 =10,(2a-b)2 =2,分别求下列代数式的值:
(1)4a2+b2 ;
(2)4a2-6ab+b2 ;
(3)16a4+b4 .
题型四:利用乘法公式解决图形面积问题
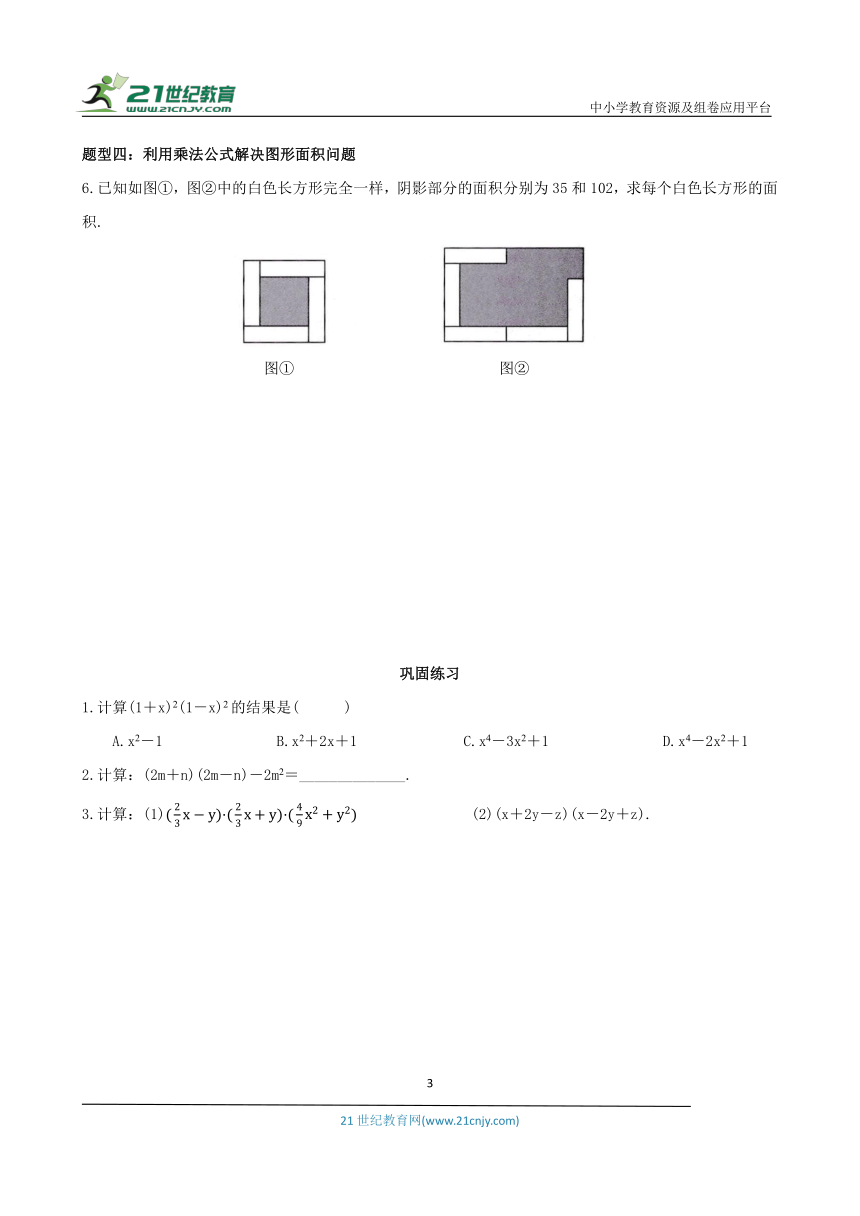
6.已知如图①,图②中的白色长方形完全一样,阴影部分的面积分别为35和102,求每个白色长方形的面积.
图① 图②
巩固练习
1.计算(1+x)2(1-x)2的结果是( )
A.x2-1 B.x2+2x+1 C.x4-3x2+1 D.x4-2x2+1
2.计算:(2m+n)(2m-n)-2m2=______________.
3.计算:(1) (2)(x+2y-z)(x-2y+z).
4.如图,小唯家计划用长为140 m的篱笆围一个长方形院子(即长方形ABCD).以AB,AD为边分别向外作正方形ABEF、正方形ADGH,并在两块正方形空地上种植不同品种的农作物,其种植面积和为2500 m2,求长方形院子ABCD的面积.
5.先化简,再求值:(m+3n)2-(2m+n)(2m-n)+2n(2m-3n),其中m=,n=.
6.已知x+y=7,xy=5,求下列代数式的值:
(1)x2-3xy+y2;
(2)x4+y4.
7.(代数推理)若m≠0,Q=(m2-m+1)(m2+m+1),P=(m+1)2(m-1)2.试说明:Q>P.
专题拓展六 参考答案
1.解:原式=(1000+2)(1000-2)-9992=10002-4-9992=(1000+999)(1000-999)-4
=1999-4=1995.
2.解:(2a+1)(2a-1)-(2a-3)2+5=4a2-1-(4a2-12a+9)+5=4a2-1-4a2+12a-9+5=12a-5,
当a=时,原式=12×-5=4-5=-1.
3.解:(2x-y)2-(x-y)(x+y)=4x2-4xy+y2-x2+y2=3x2-4xy+2y2,
因为|x+1|+(y-2)2=0,所以x=-1,y=2,
将x=-1,y=2代入,得原式=3+8+8=19.
4.解:原式=[2m+(n-1)][2m-(n-1)]=(2m)2-(n-1)2=4m2-(n2-2n+1)=4m2-n2+2n-1,
因为4m2+2n=4+n2,所以原式=4+n2-n2-1=3.
5.解:(1)因为(2a+b)2=4a2+4ab+b2=10,(2a-b)2=4a2-4ab+b2=2,
所以(2a+b)2-(2a-b)2=8ab=10-2=8,所以ab=1,
所以4a2+b2=(2a+b)2-4ab=6;
(2)由(1)可得4a2+b2=6,ab=1,所以4a2-6ab+b2=6-6=0;
(3)由(1)可得4a2+b2=6,ab=1,
所以16a4+b4=(4a2)2+(b2)2=(4a2+b2)-8a2b2=(4a2+b2)2-8(ab)2=36-8=28.
6.解:设每个白色长方形的长为a,宽为b,
由题图①可得(a+b)2-4ab=35,即a2+b2=2ab+35①,
由题图②可得(2a+b)(a+2b)-5ab=102,即a2+b2=51②.
由①②得2ab+35=51,所以ab=8,即每个白色长方形的面积为8.
巩固练习 参考答案
1.D
2.2m2-n2
3.解:(1)原式=(x2-y2)·(x2+y2)=x4-y4;
(2)原式=[x+(2y-z)][x-(2y-z)]=x2-(2y-z)2=x2-(4y2-4yz+z2)=x2-4y2+4yz-z2.
4.解:设AB=x m,AD=y m,则2(x+y)=140,所以x+y=70,
因为x2+y2=2500,所以2xy=(x+y)2-(x2+y2)=702-2500=2400,
所以xy=1200,故长方形院子ABCD的面积为1200 m2.
5.解:原式=m2+6mn+9n2-4m2+n2+4mn-6n2=-3m2+10mn+4n2,
当m=,n=时,原式=-1
6.解:(1)因为x+y=7,xy=5,所以x2-3xy+y2=(x+y)2-5xy=72-5×5=24;
(2)因为x+y=7,xy=5,
所以x2+y2=(x+y)2-2xy=72-2×5=39,所以x4+y4=(x2+y2)2-2x2y2=392-2×52=1471.
7.解:Q=(m2-m+1)(m2+m+1)=[(m2+1)-m][(m2+1)+m]=(m2+1)2-m2=m4+m2+1,
P=(m+1)2(m-1)2=(m2-1)2=m4-2m2+1,
因为m4+m4+1-(m4-2m2+1)=3m2(m≠0),所以Q-P>0,所以Q>P.
21世纪教育网(www.21cnjy.com)
专题拓展六:乘法公式的拓展应用
知识点拨:
乘法公式是初中数学中的重要公式,也是中考常见的考点之一.
平方差公式:(a+b)(a-b)=a2-b2,公式的左边是两个数的和乘这两个数的差,右边正好是这两个数的平方差,两边都有差的运算,关键要准确把握谁减去谁.
完全平方公式:(a+b)2=a2+2ab+b2,(a-b)=a2-2ab+b2,公式的左边是两个数的和(或差)的平方,右边是这两个数的平方和,再加上(或减去)这两个数积的2倍,两边的符号是一致的,要准确把握符号问题.
在解决问题时,要注意观察式子的特点,选择合适的方法和解题思路,不要拘泥于公式的形式,而要深刻理解,加以灵活运用.
完全平方公式的常见变形有:
a2+b2=(a+b)2-2ab=(a-b)2+2ab;
ab=
(a+b)2+(a-b)2 =_______________ .
题型分析
题型一:巧用乘法公式简便计算
1.计算:1002×998-9992 .
题型二:利用乘法公式化简求值
2.先化简,再求值:(2a+1)(2a-1)-(2a-3)2+5,其中a=.
3.先化简,再求值:(2x-y)2-(x-y)(x+y),其中|x+1|+(y-2)2 =0 .
4.先化简,再求值:(2m+n-1)(2m-n+1),其中4m2+2n=4+n2 .
题型三:利用乘法公式求代数式的值
5.已知(2a+b)2 =10,(2a-b)2 =2,分别求下列代数式的值:
(1)4a2+b2 ;
(2)4a2-6ab+b2 ;
(3)16a4+b4 .
题型四:利用乘法公式解决图形面积问题
6.已知如图①,图②中的白色长方形完全一样,阴影部分的面积分别为35和102,求每个白色长方形的面积.
图① 图②
巩固练习
1.计算(1+x)2(1-x)2的结果是( )
A.x2-1 B.x2+2x+1 C.x4-3x2+1 D.x4-2x2+1
2.计算:(2m+n)(2m-n)-2m2=______________.
3.计算:(1) (2)(x+2y-z)(x-2y+z).
4.如图,小唯家计划用长为140 m的篱笆围一个长方形院子(即长方形ABCD).以AB,AD为边分别向外作正方形ABEF、正方形ADGH,并在两块正方形空地上种植不同品种的农作物,其种植面积和为2500 m2,求长方形院子ABCD的面积.
5.先化简,再求值:(m+3n)2-(2m+n)(2m-n)+2n(2m-3n),其中m=,n=.
6.已知x+y=7,xy=5,求下列代数式的值:
(1)x2-3xy+y2;
(2)x4+y4.
7.(代数推理)若m≠0,Q=(m2-m+1)(m2+m+1),P=(m+1)2(m-1)2.试说明:Q>P.
专题拓展六 参考答案
1.解:原式=(1000+2)(1000-2)-9992=10002-4-9992=(1000+999)(1000-999)-4
=1999-4=1995.
2.解:(2a+1)(2a-1)-(2a-3)2+5=4a2-1-(4a2-12a+9)+5=4a2-1-4a2+12a-9+5=12a-5,
当a=时,原式=12×-5=4-5=-1.
3.解:(2x-y)2-(x-y)(x+y)=4x2-4xy+y2-x2+y2=3x2-4xy+2y2,
因为|x+1|+(y-2)2=0,所以x=-1,y=2,
将x=-1,y=2代入,得原式=3+8+8=19.
4.解:原式=[2m+(n-1)][2m-(n-1)]=(2m)2-(n-1)2=4m2-(n2-2n+1)=4m2-n2+2n-1,
因为4m2+2n=4+n2,所以原式=4+n2-n2-1=3.
5.解:(1)因为(2a+b)2=4a2+4ab+b2=10,(2a-b)2=4a2-4ab+b2=2,
所以(2a+b)2-(2a-b)2=8ab=10-2=8,所以ab=1,
所以4a2+b2=(2a+b)2-4ab=6;
(2)由(1)可得4a2+b2=6,ab=1,所以4a2-6ab+b2=6-6=0;
(3)由(1)可得4a2+b2=6,ab=1,
所以16a4+b4=(4a2)2+(b2)2=(4a2+b2)-8a2b2=(4a2+b2)2-8(ab)2=36-8=28.
6.解:设每个白色长方形的长为a,宽为b,
由题图①可得(a+b)2-4ab=35,即a2+b2=2ab+35①,
由题图②可得(2a+b)(a+2b)-5ab=102,即a2+b2=51②.
由①②得2ab+35=51,所以ab=8,即每个白色长方形的面积为8.
巩固练习 参考答案
1.D
2.2m2-n2
3.解:(1)原式=(x2-y2)·(x2+y2)=x4-y4;
(2)原式=[x+(2y-z)][x-(2y-z)]=x2-(2y-z)2=x2-(4y2-4yz+z2)=x2-4y2+4yz-z2.
4.解:设AB=x m,AD=y m,则2(x+y)=140,所以x+y=70,
因为x2+y2=2500,所以2xy=(x+y)2-(x2+y2)=702-2500=2400,
所以xy=1200,故长方形院子ABCD的面积为1200 m2.
5.解:原式=m2+6mn+9n2-4m2+n2+4mn-6n2=-3m2+10mn+4n2,
当m=,n=时,原式=-1
6.解:(1)因为x+y=7,xy=5,所以x2-3xy+y2=(x+y)2-5xy=72-5×5=24;
(2)因为x+y=7,xy=5,
所以x2+y2=(x+y)2-2xy=72-2×5=39,所以x4+y4=(x2+y2)2-2x2y2=392-2×52=1471.
7.解:Q=(m2-m+1)(m2+m+1)=[(m2+1)-m][(m2+1)+m]=(m2+1)2-m2=m4+m2+1,
P=(m+1)2(m-1)2=(m2-1)2=m4-2m2+1,
因为m4+m4+1-(m4-2m2+1)=3m2(m≠0),所以Q-P>0,所以Q>P.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
