5.3.2函数的极值与最大(小)值+(1)+课件(共16张PPT)-2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 5.3.2函数的极值与最大(小)值+(1)+课件(共16张PPT)-2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 12:11:00 | ||
图片预览



文档简介
(共16张PPT)
5.3.2 函数的极值与最大(小)值 (1)
第五章 一元函数的导数及其应
增
减
温故知新
我们发现利用导数的正负可以判断函数的增减.
如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
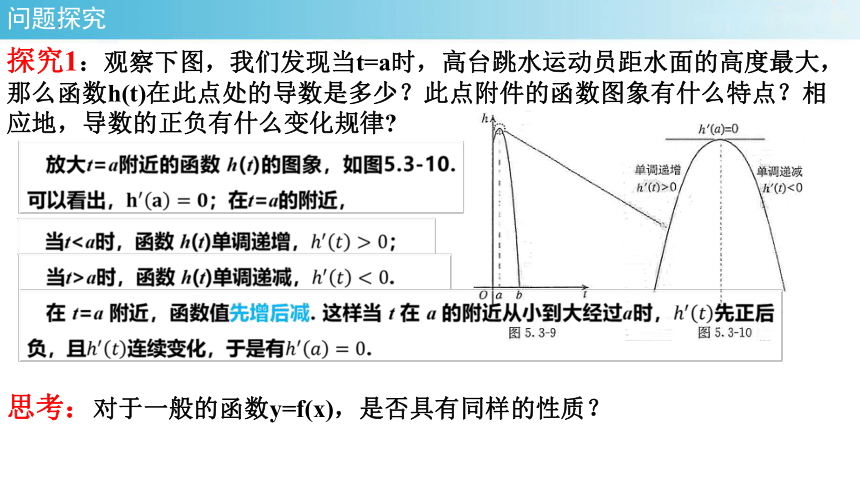
探究1:观察下图,我们发现当t=a时,高台跳水运动员距水面的高度最大,那么函数h(t)在此点处的导数是多少?此点附件的函数图象有什么特点?相应地,导数的正负有什么变化规律
问题探究
思考:对于一般的函数y=f(x),是否具有同样的性质?
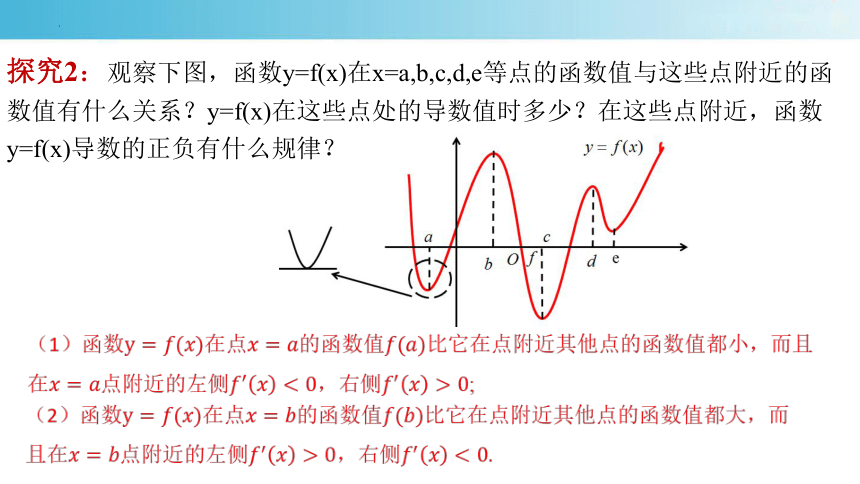
探究2:观察下图,函数y=f(x)在x=a,b,c,d,e等点的函数值与这些点附近的函数值有什么关系?y=f(x)在这些点处的导数值时多少?在这些点附近,函数y=f(x)导数的正负有什么规律?
概念解析
1.极小值点与极小值
若函数f(x)满足:
(1)在x=a附近其他点的函数值f(x)≥f(a).
(2)f′(a)=0.
(3)在x=a附近的左侧f′(x)<0,右侧f′(x)>0.
则a叫做函数y=f(x)的_________,f(a)叫做函数y=f(x)的_______.
极小值点
极小值
2.极大值点与极大值
若函数f(x)满足:
(1)在x=b附近其他点的函数值f(x)≤f(b).
(2)f′(b)=0.
(3)在x=b附近的左侧f′(x)>0,右侧f′(x)<0.
则b叫做函数y=f(x)的_________,f(b)叫做函数y=f(x)的_______.
极大值点
极大值
3.极值点、极值的定义
(1)极小值点、极大值点统称为极值点.
(2)极小值、极大值统称为极值.
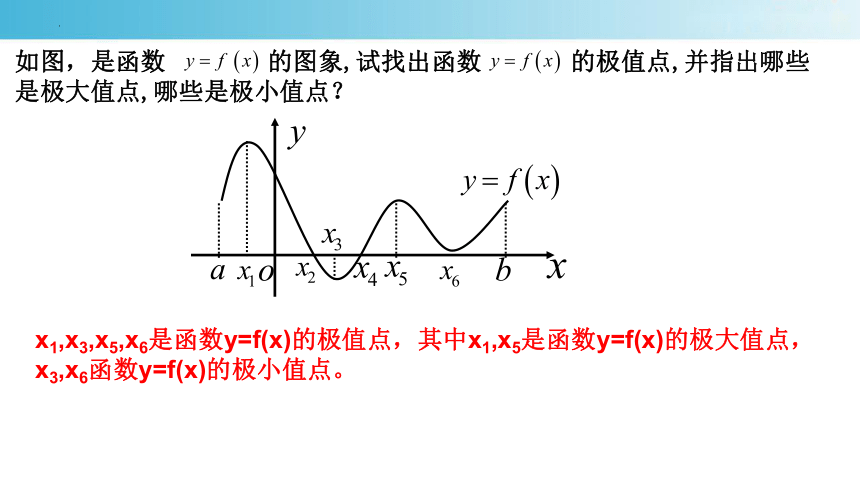
x1,x3,x5,x6是函数y=f(x)的极值点,其中x1,x5是函数y=f(x)的极大值点,x3,x6函数y=f(x)的极小值点。
如图,是函数 的图象,试找出函数 的极值点,并指出哪些是极大值点,哪些是极小值点?
思考:
(1)函数的极小值点是点吗
(2)函数的极小值唯一吗
(3)函数的极大值一定大于它的极小值吗
(4)函数区间的端点能为极值点吗
函数的极小值点不是点,它是函数极小值对应的自变量的值.
不一定,有的函数无极小值,有的函数只有一个极小值,有的函数有多个极小值.
不一定.
不能.
典例解析
方法总结:求函数y=f(x)极值的方法
定义域
求导
求零点
列表
求极值
(1)求定义域及f′(x)
(2)求f′(x)=0在函数定义域内的所有根;
(3)用方程f′(x)=0的根将定义域分成若干小区间,列表;
(4)由f′(x)在各个小区间内的符号,判断函数的极值情况.
思考:若f′(x0)=0,函数y=f(x)在x=x0处一定取得极值吗
不一定.例如f(x)=x3,x=0时,f′(0)=0,但由于在x=0两侧导数同号,因此
函数f(x)=x3在x=0处不取得极值.
注意:f /(x0)=0是函数取得极值的必要不充分条件
跟踪训练
2.已知函数 在 处取得极值。
(1)求函数 的解析式
(2)求函数 的单调区间
解:(1)
∵ 在 取得极值, ∴
即 解得
∴
(2) ∵ , 由 得
∴ 的单调增区间为
由 得
的单调减区间为
1、函数的极值与导数的关系
(1)函数的极小值与极小值点
若函数f(x)在点x=a处的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0,而且在点x=a附近的左侧f′(x)<0,右侧f′(x)>0,则点a叫做函数的极小值点,f(a)叫做函数的极小值.
(2)函数的极大值与极大值点
若函数f(x)在点x=b处的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0,而且在点x=b附近的左侧f′(x)>0,右侧f′(x)<0,则点b叫做函数的极大值点,f(b)叫做函数的极大值.
课堂总结
2.求解函数极值的一般步骤:
(1)求函数的定义域;
左正右负极大值;
左负右正极小值.
5.3.2 函数的极值与最大(小)值 (1)
第五章 一元函数的导数及其应
增
减
温故知新
我们发现利用导数的正负可以判断函数的增减.
如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
探究1:观察下图,我们发现当t=a时,高台跳水运动员距水面的高度最大,那么函数h(t)在此点处的导数是多少?此点附件的函数图象有什么特点?相应地,导数的正负有什么变化规律
问题探究
思考:对于一般的函数y=f(x),是否具有同样的性质?
探究2:观察下图,函数y=f(x)在x=a,b,c,d,e等点的函数值与这些点附近的函数值有什么关系?y=f(x)在这些点处的导数值时多少?在这些点附近,函数y=f(x)导数的正负有什么规律?
概念解析
1.极小值点与极小值
若函数f(x)满足:
(1)在x=a附近其他点的函数值f(x)≥f(a).
(2)f′(a)=0.
(3)在x=a附近的左侧f′(x)<0,右侧f′(x)>0.
则a叫做函数y=f(x)的_________,f(a)叫做函数y=f(x)的_______.
极小值点
极小值
2.极大值点与极大值
若函数f(x)满足:
(1)在x=b附近其他点的函数值f(x)≤f(b).
(2)f′(b)=0.
(3)在x=b附近的左侧f′(x)>0,右侧f′(x)<0.
则b叫做函数y=f(x)的_________,f(b)叫做函数y=f(x)的_______.
极大值点
极大值
3.极值点、极值的定义
(1)极小值点、极大值点统称为极值点.
(2)极小值、极大值统称为极值.
x1,x3,x5,x6是函数y=f(x)的极值点,其中x1,x5是函数y=f(x)的极大值点,x3,x6函数y=f(x)的极小值点。
如图,是函数 的图象,试找出函数 的极值点,并指出哪些是极大值点,哪些是极小值点?
思考:
(1)函数的极小值点是点吗
(2)函数的极小值唯一吗
(3)函数的极大值一定大于它的极小值吗
(4)函数区间的端点能为极值点吗
函数的极小值点不是点,它是函数极小值对应的自变量的值.
不一定,有的函数无极小值,有的函数只有一个极小值,有的函数有多个极小值.
不一定.
不能.
典例解析
方法总结:求函数y=f(x)极值的方法
定义域
求导
求零点
列表
求极值
(1)求定义域及f′(x)
(2)求f′(x)=0在函数定义域内的所有根;
(3)用方程f′(x)=0的根将定义域分成若干小区间,列表;
(4)由f′(x)在各个小区间内的符号,判断函数的极值情况.
思考:若f′(x0)=0,函数y=f(x)在x=x0处一定取得极值吗
不一定.例如f(x)=x3,x=0时,f′(0)=0,但由于在x=0两侧导数同号,因此
函数f(x)=x3在x=0处不取得极值.
注意:f /(x0)=0是函数取得极值的必要不充分条件
跟踪训练
2.已知函数 在 处取得极值。
(1)求函数 的解析式
(2)求函数 的单调区间
解:(1)
∵ 在 取得极值, ∴
即 解得
∴
(2) ∵ , 由 得
∴ 的单调增区间为
由 得
的单调减区间为
1、函数的极值与导数的关系
(1)函数的极小值与极小值点
若函数f(x)在点x=a处的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0,而且在点x=a附近的左侧f′(x)<0,右侧f′(x)>0,则点a叫做函数的极小值点,f(a)叫做函数的极小值.
(2)函数的极大值与极大值点
若函数f(x)在点x=b处的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0,而且在点x=b附近的左侧f′(x)>0,右侧f′(x)<0,则点b叫做函数的极大值点,f(b)叫做函数的极大值.
课堂总结
2.求解函数极值的一般步骤:
(1)求函数的定义域;
左正右负极大值;
左负右正极小值.
