人教版七年级下册6.2立方根课件(共21张PPT)
文档属性
| 名称 | 人教版七年级下册6.2立方根课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 298.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 21:20:24 | ||
图片预览








文档简介
(共21张PPT)
6.2 立方根
七年级数学(下册) 人教版
七年级数学组
主 备 人:
议课组长:
议课日期:2023.3.7
授课日期:
第六章 实数
课前提问(1分钟)
1、平方根的定义是什么?如何表示?
解:一般地,如果一个数x的平方等于a,即_______,
那么这个数___就叫做___的平方根.
x2=a
x
a
3、平方根的性质是什么?
2、 a(a≥0)的平方根表示为:________
解:正数的平方根有___个,它们互为_________;
0的平方根是______;
负数____平方根 .
两
相反数
0
没有
x3=a
x
如果变成 ,
又叫做什么呢?
±
学习目标(1分钟)
1、掌握立方根的概念与性质,会用符号表示一个数的立方根。
3、能利用开立方解决实际问题.
2、会求一个数的立方根;
情景引入
要制作一种容积为27 m 的正方体形状的包装箱,这种包装箱的棱长应该是多少?
设这种包装箱的棱长为x m,
则
即 x x x=27
而所以x=3
则这种包装箱的棱长应该是3 m
解:
答:这种包装箱的棱长应该是3m.
认真阅读课本P49-P50的内容,完成:
1.什么叫立方根?
2.什么叫开立方?开立方与立方有什么关系?
3.如何表示一个数a的立方根?这里a可以是负数吗?
4.立方根的性质:
________都有立方根,而且只有一个;正数的立方根是____数;
负数的立方根是____数;0的立方根是____.
5.平方根与立方根有何不同?
正
负
0
互为逆运算
任何数
自学指导1:(5分钟)
5的立方根记作____,-5的立方根记作_____
0的立方根记作____
2.平方根的性质
一个正数有两个平方根;0只有一个平方根,它是0本身;负数没有平方根.
2.立方根的性质
正数的立方根是正数;负数的
立方根是负数;0的立方根是0.
一个数只有唯一的一个立方根.
1.开平方的定义
求一个数a的平方根的运算,叫做开平方,其中a叫做被开方数如:
求一个数a的立方根的运算,叫做开立方,其中a叫做被开方数
如:
1.开立方的定义
定义
性质
特别注意:
平方根与立方根
3.一个数的立方根可能是有理数,也可能是无理数
如 , 是无理数.
是有理数
比一比
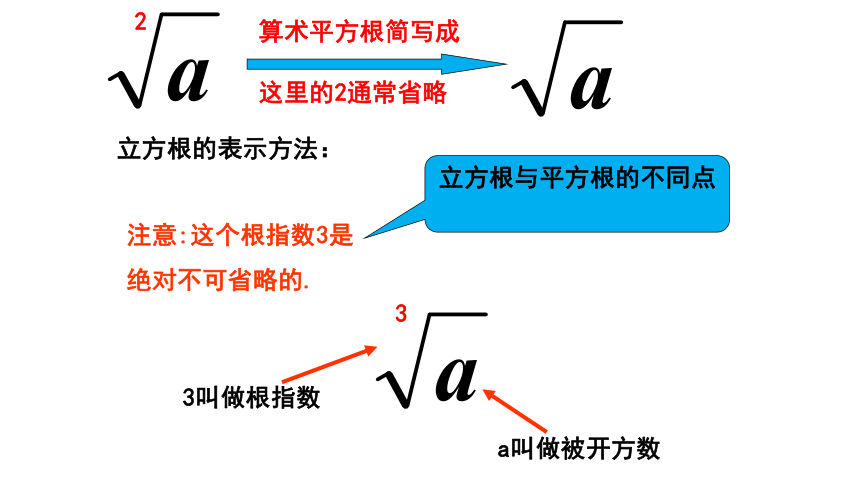
立方根的表示方法:
注意:这个根指数3是
绝对不可省略的.
3叫做根指数
a叫做被开方数
立方根与平方根的不同点
算术平方根简写成
这里的2通常省略
2
3
1.下列说法正确的是( )
平方根等于它本身的是______,
B
0
0和±1
A.一个数的立方根有两个,它们互为相反数
B.一个数的立方根与这个数同号
C.一个数的平方根一定大于这个数的立方根
D.一个数的立方根一定小于这个数
自学检测1:(3分钟)
立方根等于它本身的是________.
2. 算术平方根等于它本身的是_______
0和1
自学指导2:(5分钟)
认真阅读课本P50的例1,完成下列任务:
1.会求一个数的立方根,并会表示.
2.仿例题,做习题,完成P51习题1
2.判断下列说法对不对?
(1)-4没有立方根
(2)1的立方根是
(3)-5的立方根是
(4)64的算术平方根是8
1.求下列各数的立方根:
(1)64 (2) -27 (3) 0
(4) 3 (5) -0.008 (6)
自学检测2:(5分钟)
4
-3
0
×
-0.2
×
√
√
4、立方根是 的数是________
是________的立方根
3.下列说法中正确的是( )
的立方根是± B. 的立方根是-1
的立方根是4 D.-3是-27的立方根.
D
-2
-2
-3
-3
自学指导3(4分钟)
自学课本P50的探究
结合立方根的性质,完成下列任务:
(1) =( ) (2) =( )
(3) =( )(4) =( )
结合立方根的性质,完成下列任务
(1) =( )(2) =( )
(3) =( ) (4) =( )
2
-2
3
-3
(1) =( ) (2) =( )
(3) =( ) (4) =( )
8
-27
64
-64
自学检测3:(5分钟)
1.求下列各式的值:
(1) (2)
(3) (4)
2.若5x+19的立方根为4,求3x+9的平方根.
3.求下列各式中的x的值.
(1)8x3+27=0 (2)2(x-5)3=-128
4.x取何值时,下面各式有意义?
(1) (2)
(3) (4)
(1)符号 中根指数“3”不能省略;
(2)任何数都只有一个立方根,且开方前后符号不变;
(3)平方根和立方根的区别:
正数有两个平方根,但只有一个立方根,
负数没有平方根,但却有一个立方根;
(4)灵活运用式:
(5)立方与开立方也互为逆运算.我们也可以用立方运算求一个数的立方根,或检验一个数是不是另一个数的立方根.
小结:(1分钟)
算术平方根、平方根及立方根的区别与联系
a为0 a为负数 a为正数
算术平方根 0 无
平方根 0 无
立方根
被开方数a
操作
1个
2个
1个
0
当堂训练:(15分钟)
1.判断题
(1)如果b是a的三次幂,那么b的立方根是a ( )
(2)任何正数都有两个立方根, 它们互为相反数( )
(3)负数没有立方根 ( )
(4)如果a是b的立方根,那么ab≥0 ( )
(5) 的立方根是3 ( )
(6) 的立方根是±3 ( )
2.求下列各式的值(注意格式的书写).
√
×
√
×
×
×
3.下列各组数中表示相同的一组是( ).
A. 与 B. 与
C. 与 D. 2 与
4.下列计正确的是( ).
A. B.
C. D.
C
B
5、解方程:
6、若5x+19的立方根为4,求3x+9的平方根.
解:由题可得:5x+19=43
x=9
将x=9代入,得 3x+9=3×9+9=36
∵(±6)2=36
∴ 3x+9的平方根是±6
C
(选做题)
A. B. C. D.0
5.解方程.
1.立方根的定义: 一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根
板书设计
2.立方根的性质:正数的立方根是正数;
负数的立方根是负数;
0的立方根是0.
一个数只有唯一的一个立方根.
3.灵活运用公式:
6.2 立方根
七年级数学(下册) 人教版
七年级数学组
主 备 人:
议课组长:
议课日期:2023.3.7
授课日期:
第六章 实数
课前提问(1分钟)
1、平方根的定义是什么?如何表示?
解:一般地,如果一个数x的平方等于a,即_______,
那么这个数___就叫做___的平方根.
x2=a
x
a
3、平方根的性质是什么?
2、 a(a≥0)的平方根表示为:________
解:正数的平方根有___个,它们互为_________;
0的平方根是______;
负数____平方根 .
两
相反数
0
没有
x3=a
x
如果变成 ,
又叫做什么呢?
±
学习目标(1分钟)
1、掌握立方根的概念与性质,会用符号表示一个数的立方根。
3、能利用开立方解决实际问题.
2、会求一个数的立方根;
情景引入
要制作一种容积为27 m 的正方体形状的包装箱,这种包装箱的棱长应该是多少?
设这种包装箱的棱长为x m,
则
即 x x x=27
而所以x=3
则这种包装箱的棱长应该是3 m
解:
答:这种包装箱的棱长应该是3m.
认真阅读课本P49-P50的内容,完成:
1.什么叫立方根?
2.什么叫开立方?开立方与立方有什么关系?
3.如何表示一个数a的立方根?这里a可以是负数吗?
4.立方根的性质:
________都有立方根,而且只有一个;正数的立方根是____数;
负数的立方根是____数;0的立方根是____.
5.平方根与立方根有何不同?
正
负
0
互为逆运算
任何数
自学指导1:(5分钟)
5的立方根记作____,-5的立方根记作_____
0的立方根记作____
2.平方根的性质
一个正数有两个平方根;0只有一个平方根,它是0本身;负数没有平方根.
2.立方根的性质
正数的立方根是正数;负数的
立方根是负数;0的立方根是0.
一个数只有唯一的一个立方根.
1.开平方的定义
求一个数a的平方根的运算,叫做开平方,其中a叫做被开方数如:
求一个数a的立方根的运算,叫做开立方,其中a叫做被开方数
如:
1.开立方的定义
定义
性质
特别注意:
平方根与立方根
3.一个数的立方根可能是有理数,也可能是无理数
如 , 是无理数.
是有理数
比一比
立方根的表示方法:
注意:这个根指数3是
绝对不可省略的.
3叫做根指数
a叫做被开方数
立方根与平方根的不同点
算术平方根简写成
这里的2通常省略
2
3
1.下列说法正确的是( )
平方根等于它本身的是______,
B
0
0和±1
A.一个数的立方根有两个,它们互为相反数
B.一个数的立方根与这个数同号
C.一个数的平方根一定大于这个数的立方根
D.一个数的立方根一定小于这个数
自学检测1:(3分钟)
立方根等于它本身的是________.
2. 算术平方根等于它本身的是_______
0和1
自学指导2:(5分钟)
认真阅读课本P50的例1,完成下列任务:
1.会求一个数的立方根,并会表示.
2.仿例题,做习题,完成P51习题1
2.判断下列说法对不对?
(1)-4没有立方根
(2)1的立方根是
(3)-5的立方根是
(4)64的算术平方根是8
1.求下列各数的立方根:
(1)64 (2) -27 (3) 0
(4) 3 (5) -0.008 (6)
自学检测2:(5分钟)
4
-3
0
×
-0.2
×
√
√
4、立方根是 的数是________
是________的立方根
3.下列说法中正确的是( )
的立方根是± B. 的立方根是-1
的立方根是4 D.-3是-27的立方根.
D
-2
-2
-3
-3
自学指导3(4分钟)
自学课本P50的探究
结合立方根的性质,完成下列任务:
(1) =( ) (2) =( )
(3) =( )(4) =( )
结合立方根的性质,完成下列任务
(1) =( )(2) =( )
(3) =( ) (4) =( )
2
-2
3
-3
(1) =( ) (2) =( )
(3) =( ) (4) =( )
8
-27
64
-64
自学检测3:(5分钟)
1.求下列各式的值:
(1) (2)
(3) (4)
2.若5x+19的立方根为4,求3x+9的平方根.
3.求下列各式中的x的值.
(1)8x3+27=0 (2)2(x-5)3=-128
4.x取何值时,下面各式有意义?
(1) (2)
(3) (4)
(1)符号 中根指数“3”不能省略;
(2)任何数都只有一个立方根,且开方前后符号不变;
(3)平方根和立方根的区别:
正数有两个平方根,但只有一个立方根,
负数没有平方根,但却有一个立方根;
(4)灵活运用式:
(5)立方与开立方也互为逆运算.我们也可以用立方运算求一个数的立方根,或检验一个数是不是另一个数的立方根.
小结:(1分钟)
算术平方根、平方根及立方根的区别与联系
a为0 a为负数 a为正数
算术平方根 0 无
平方根 0 无
立方根
被开方数a
操作
1个
2个
1个
0
当堂训练:(15分钟)
1.判断题
(1)如果b是a的三次幂,那么b的立方根是a ( )
(2)任何正数都有两个立方根, 它们互为相反数( )
(3)负数没有立方根 ( )
(4)如果a是b的立方根,那么ab≥0 ( )
(5) 的立方根是3 ( )
(6) 的立方根是±3 ( )
2.求下列各式的值(注意格式的书写).
√
×
√
×
×
×
3.下列各组数中表示相同的一组是( ).
A. 与 B. 与
C. 与 D. 2 与
4.下列计正确的是( ).
A. B.
C. D.
C
B
5、解方程:
6、若5x+19的立方根为4,求3x+9的平方根.
解:由题可得:5x+19=43
x=9
将x=9代入,得 3x+9=3×9+9=36
∵(±6)2=36
∴ 3x+9的平方根是±6
C
(选做题)
A. B. C. D.0
5.解方程.
1.立方根的定义: 一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根
板书设计
2.立方根的性质:正数的立方根是正数;
负数的立方根是负数;
0的立方根是0.
一个数只有唯一的一个立方根.
3.灵活运用公式:
