北师大版六年级下册第四单元《正比例与反比例》单元专项训练——应用题(含答案+详细解析)
文档属性
| 名称 | 北师大版六年级下册第四单元《正比例与反比例》单元专项训练——应用题(含答案+详细解析) |  | |
| 格式 | doc | ||
| 文件大小 | 689.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-12 17:27:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版小学数学六年级下册
第四单元《正比例与反比例》单元专项训练——应用题
1.在比例尺为1∶10000000的地图上,量得甲地到乙地的高速铁路长6.6厘米。高速铁路上的火车平均运行速度为210千米/时,从甲地到乙地乘火车大约需几小时?(得数保留一位小数)
2.用一些纸装订同样的练习本,每本用纸的张数和装订的本数如下表。
每本用纸张数/张 8 10 15 20 24
装订本数/本 75 60 40
(1)将上表补充完整。
(2)每本用纸张数和装订本数是不是成反比例?说明理由。
(3)如果用这些纸装订成50本练习本(每本用纸张数相同),每本用纸多少张?
3.购买一种笔筒的数量和应付金额如下表。
数量/个 0 1 2 3 4 5 …
应付金额/元业 0 8 16 24 32 40 …
(1)判断应付金额与笔筒的数量是否成正比例关系,并说明理由。
(2)先把上表中数量和应付金额所对应的点描在方格纸上,再顺次连接。
(3)买20个笔筒需要( )元,144元最多可以买( )个这样的笔筒。
4.某环保节能造纸厂造纸总量与所用时间如下表。
时间/天 0 1 2 3 4 5 …
生产总量/吨 0 12 24 36 48 60 …
(1)生产总量和时间成正比例关系吗?说明理由。
(2)在下图中描出时间与生产总量对应的点,再顺次连接。
(3)8天可以生产( )吨纸,生产90吨纸需要( )天。
5.学校买来一批打印纸,计划每天用200张,可用45天,实际节约用纸后,每天少用了50张,实际这些打印纸多用了多少天?
6.甲、乙两地相距520千米。一辆汽车从甲地开往乙地,4时行驶了160千米。照这样的速度,这辆汽车从甲地到乙地需要开几小时?(用比例解)
7.造纸术是中国四大发明之一,是中华民族对世界文明的巨大贡献,是人类文明史上的一项杰出的发明创造。某造纸厂的生产情况如下表,根据表回答问题。
时间(天) 0 1 2 3 4 5 6 7 …
生产量(吨) 0 70 140 210 280 350 420 490 …
(1)生产量和所用时间成正比例关系吗?为什么?
(2)根据表中的数据,写出一个比例( )。
(3)在下图中描出表示时间和相应生产量对应的点,并把它们按顺序连接起来。
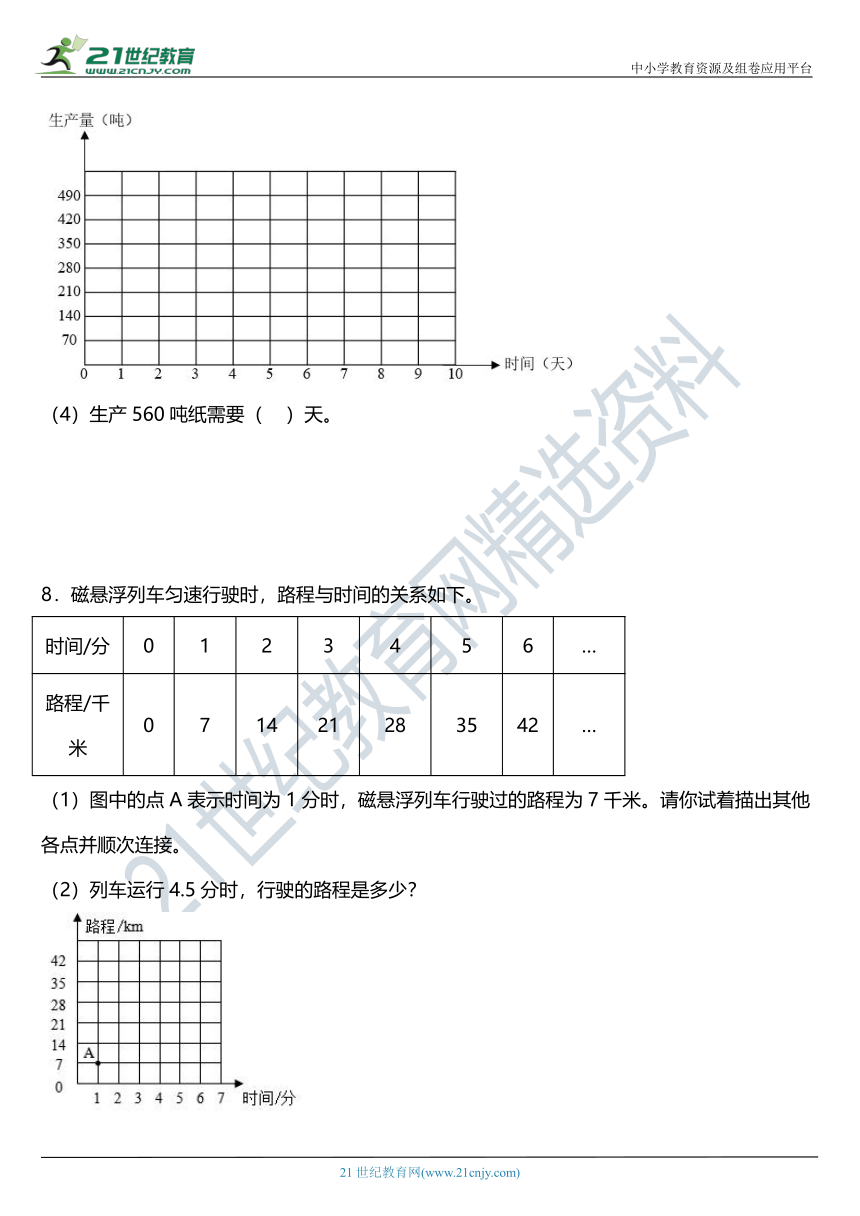
(4)生产560吨纸需要( )天。
8.磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 0 1 2 3 4 5 6 …
路程/千米 0 7 14 21 28 35 42 …
(1)图中的点A表示时间为1分时,磁悬浮列车行驶过的路程为7千米。请你试着描出其他各点并顺次连接。
(2)列车运行4.5分时,行驶的路程是多少?
9.输液时,一小瓶葡萄糖液均匀滴落,每分滴数与所需时间的关系如下。
每分滴数/滴 30 40 50 60 …
时间/分 40 30 …
(1)请把上表补充完整。
(2)每分滴数与所需时间这两个量是否成正比例或反比例?为什么?
10.下面是某超市一种大米的质量和总价的统计表。
质量/千克 0 5 10 15 20 25 30
总价/元 0 20 40 60 80
(1)先把上表填写完整,再把大米的质量与总价所对应的点在下图中描出来,并连线。
(2)大米的质量与总价成正比例关系吗?为什么?
(3)张阿姨买这种大米的总价是李阿姨的4倍,张阿姨买的大米的质量是李阿姨的( )倍。
11.有一个甘蔗榨汁机,可以用500克的甘蔗榨出150克的甘蔗汁,现在有10千克的甘蔗,可以榨出多少克甘蔗汁?(用比例解答)
12.一辆卡车运一堆木材,如果每次运60根,15次刚好可以运完;如果每次运75根,多少次可完?(用比例知识解答)
13.某条船的乘船人数与所付船费如下表。
乘船人数/人 0 1 2 3 4 5 6 …
所付船费/元 0 5 10 15 20 …
(1)判断这条船的乘船人数与所付船费是不是成正比例,并说明理由。
(2)先将上面的表格填写完整,再根据表中数据,在下图中描出这条船的乘船人数与所付船费所对应的点,再把这些点依次连接起来。
(3)如果这条船乘坐了12人,那么所付船费是( )元;付105元船费可乘坐( )人。
14.某工厂有一批煤,每天烧煤的质量和可烧的时间关系如下表。
每天烧煤的质量/吨 0 3 6 9 15 20 …
可烧的时间/天 0 30 15 10 6 4.5 …
(1)判断每天烧煤的质量和可烧的时间是不是成反比例,并说明理由。
(2)如果该工厂平均每天烧煤的质量是5吨,那么这批煤可烧多少天?
15.张师傅加工一批玩具时,加工时间与数量的变化情况如下表。
加工时间/时 0 1 2 3 4 5 …
加工数量/个 0 12 24 36 48 60 …
(1)加工玩具的数量与时间成正比例关系吗?为什么?
(2)根据表中数据,在下图,再把这些点依次连起来。
(3)加工108个玩具需要( )小时,6.5小时可以加工( )个玩具。
16.下面是某小学六(3)班订阅《少年报》的数量与总价的对应数值表。
数量/份 0 1 2 3 4 5 6 ……
总价/元 0 12 24 36 48 60 72 ……
(1)订阅《少年报》的数量与总价成正比例关系吗?为什么?
(2)在下图中描出该小学六(3)班订阅《少年报》的数量与总价的点,然后把它们按顺序连起来。
(3)该校六(1)班要订阅43份《少年报》,一共需要( )元;六(2)班订阅《少年报》一共花了468元,六(2)班订阅了( )份《少年报》。
17.李叔叔摘了一些苹果,每箱装的个数和装的箱数如下表。
每箱装的个数 12 20 30 40 50
装的箱数 200 120 80
(1)完成上表。
(2)每箱装的个数和装的箱数成反比例吗?为什么?
(3)如果装了75箱,平均每箱装了多少个?
18.某运输公司要将一批建筑材料一次运往建筑工地。每辆汽车的载质量与所需汽车的数量如下表。
每辆汽车的载质量/吨 2.5 4 5 8
所需汽车数量/辆 48 30 24 15
(1)每辆汽车的载质量与所需汽车数量成什么比例关系?
(2)如果这批建筑材料用载质量为10吨的汽车一次运完。需要多少辆汽车来运?
19.一台碾米机碾米情况如下表:
工作时间(时) 0 1 2 3 4 5
加工数量(吨) 0 0.5 1 1.5 2 2.5
(1)把上表中相对应的点描在下图中,再顺次连接。
(2)工作时间与加工数量成什么比例?为什么?
(3)现在碾米8吨,需要几小时?
20.某移动营业大厅,用边长为6分米的方砖铺地,需用200块;若改铺边长为4分米的方砖铺,需要多少块?
21.一种丝绸面料购买的长度与金额的情况如下表。
长度/米 0 1 2 3 4 5 6 7
金额/元 0 50 100 150 200 250
(1)判断这种丝绸面料购买的长度与金额是不是成正比例,并说明理由。
(2)先将上面的表格填写完整,再根据表中数据,在下图中描出这种丝绸面料购买的长度与金额所对应的点,再把这些点依次连接起来。
(3)8000元可以买( )米这种丝绸面料;购买7.5米这种丝绸面需要( )元。
22.某台榨油机的生产时间与产量的关系如下表。
生产时间/时 0 1 2 3 4 5 6 7
产量/吨 0 4 8 12 16 20 24 28
(1)先根据上表描点,再顺次连接各点。
(2)生产时间与产量成( )(填“正”或“反”)比例关系。
(3)这台榨油机榨70吨油需要( )时。
23.某工厂生产一批笔记本电脑,原计划每天生产40台,60天完成。实际每天多生产8台,实际提前多少天完成?(用比例解答)
24.根据疫情防控要求,王师傅用喷雾器对小区的公共区域进行全覆盖消毒。如果每分钟喷洒35平方米,40分钟能全部消杀一遍,现在想用28分钟完成任务,每分钟应喷洒多少平方米?(用比例知识解答)
25.晶晶去文具店购买同一支圆珠笔,购买圆珠笔的数量和总价如下表所示。
数量/支 0 1 2 3 4 5
总价/元 0 4 8 12
(1)把上表填写完整。
(2)购买圆珠笔的数量与总价成正比例吗?为什么?
(3)先根据上表描点,再顺次连接各点。
晶晶想要买12支这种圆珠笔,一共需要花费( )元;如果晶晶有70元,她最多可以买( )支这种圆珠笔。
参考答案:
1.3.1小时
【分析】已知比例尺和甲地到乙地高速铁路的图上距离,根据“实际距离=图上距离÷比例尺”,求出甲地到乙地高速铁路的实际距离,并根据进率“1千米=100000厘米”换算;然后根据“时间=路程÷速度”,求出从甲地到乙地乘火车需要的时间。
【详解】6.6÷
=6.6×10000000
=66000000(厘米)
66000000厘米=660千米
660÷210≈3.1(小时)
答:从甲地到乙地乘火车大约需3.1小时。
【点睛】本题考查比例尺的应用以及行程问题,掌握图上距离、实际距离、比例尺之间的关系,以及速度、时间、路程之间的关系是解题的关键。
2.(1)30;25
(2)成反比例;理由见详解
(3)12张
【分析】(1)8×75=10×60=15×40=600;根据积都是600,用600除以20和24即可;
(2)判断练习本每本的页数和装订的本数之间成什么比例,就看这两个量是对应的比值一定还是乘积一定;如果是比值一定,成正比例;如果是乘积一定,就成反比例;据此解答;
(3)用600除以50即可求出每本用纸多少张。
【详解】(1)8×75÷20
=600÷20
=30(本)
8×75÷24
=600÷24
=25(本)
每本用纸张数/张 8 10 15 20 24
装订本数/本 75 60 40 30 25
(2)因为8×75=10×60=15×40=20×30=24×25=600(一定)
乘积一定,所以每本用纸张数与装订本数成反比例。
(3)8×75÷50
=600÷50
=12(张)
答:每本用纸12张。
【点睛】利用正比例意义和辨识,反比例意义和辨识以及反比例的应用进行解答。
3.(1)应付金额与笔筒的数量成正比例关系,理由:应付金额与笔筒的数量的比值一定,所以应付金额与笔筒的数量成正比例关系。
(2)见详解
(3)160;18
【分析】(1)因为应付金额÷数量=单价(一定),所以应付金额与数量是成正比例关系。
(2)根据统计表中的数据描出各点,然后顺序连接各点即可。
(3)根据单价×数量=总价,总价÷单价=数量,据此列式解答。
【详解】(1)应付金额与笔筒的数量成正比例关系,理由如下:因为40∶5=32∶4=24∶3=16∶2=8∶1=8(定值),所以应付金额与笔筒的数量成正比例关系。
(2)如图:
(3)20×8=160(元)
144÷8=18(个)
买20个笔筒需要160元,144元最多可以买18个这样的笔筒。
【点睛】此题考查的目的是理解掌握正比例的意义及应用,明确:正比例的图像
4.(1)成正比例关系;理由见详解
(2)见详解
(3)96;7.5
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例;据此解答。
(2)首先根据统计表中的数据在图中描出各点,然后顺次连接各点即可。
(3)每天的生产效率×生产的天数=生产总量即可解答。
【详解】(1)生产总量和时间成正比例关系;因为12∶1=24∶2=36∶3=48∶4=60∶5=定值。所以生产总量和时间成正比例关系。
(2)作图如下:
(3)8×12=96(吨)
90÷12=7.5(天)
答:8天可以生产96吨纸,生产90吨纸需要7.5天。
【点睛】此题考查的意义是理解掌握正比例的意义及应用。
5.15天
【分析】根据题意,打印纸的总张数没有变化,找出等量关系:计划用的时间×计划每天用的张数=实际用的时间×实际每天用的张数,列方程解答。
【详解】解:设实际这些打印纸多用了x天。
(200-50)×(45+x)=200×45
150×(45+x)=9000
6750+150x=9000
150x=2250
x=15
答:实际这些打印纸多用了15天。
【点睛】本题考查有关计划与实际比较应用题的计算及应用,出数量关系,列式计算即可。
6.13小时
【分析】根据题意,速度一定,路程与时间成正比例,可得:甲、乙两地路程∶从甲地到乙地需要的时间=4小时行驶的路程∶4小时。
【详解】解:设这辆汽车从甲地到乙地需要开x小时。
520∶x=160∶4
160x=520×4
160x÷160=2080÷160
x=13
答:这辆汽车从甲地到乙地需要开13小时。
【点睛】根据速度不变列出比例,是解答此题的关键。
7.(1)成正比例关系;因为:======。
(2)1∶70=2∶140(答案不唯一)
(3)
(4)8
【分析】(1)根据生产量与生产时间的比的比值判断是不是成正比例;
(2)从表中找出两组数据,写成比例式;
(3)根据表中数据描点、连线;
(4)用560除以每天生产的吨数即可。
【详解】(1)======。
所以生产量和所用时间成正比例关系。
(2)1∶70=2∶140(答案不唯一)
(3)
(4)560÷70=8(天)
【点睛】本题考查了正比例关系的判断、写比例式、画正比例关系图像、根据正比例关系解决问题等,综合性强,需仔细更新和解答。
8.(1)见详解;
(2)31.5千米
【分析】将表中的数据进行分析,可知路程与时间的比值一定,即路程与时间成正比例关系;
(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米,可知本次列车的速度为7千米/分,依据表中数据将其他各点在图中描出即可;
(2) 列车运行4.5分时,依据路程=时间×速度,将数据代入即可行驶的路程。
【详解】(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米,依据表中数据将其他各点在图中描出。如下图:
(2)4.5×7=31.5(千米)
答:行驶的路程是31.5千米。
【点睛】本题主要考查了正比例关系的应用,掌握成正比例的量的变化规律及其特征是解答此题的关键。
9.(1)24;20
(2)成反比例;理由见解析。
【分析】(1)观察统计表可知,一小瓶葡萄糖液的滴数是一定的,即总滴数=每分钟滴的滴数×滴的时间;根据表中每分钟滴30滴、40滴时所用的时间,皆可求出一小瓶葡萄糖液的总滴数,据此即可求出每分钟滴50滴、60滴的所用时间。
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此解答。
【详解】由分析可知:
(1)30×40=1200(滴)
1200÷50=24(分)
1200÷60=20(分)
(2)成反比例,因为30×40=40×30=1200(一定),每分滴数与所需时间的乘积一定,所以每分滴数与所需时间这两个量成反比例。
【点睛】本题主要考查反比例的辨识及实际应用,通过统计表获取信息的意识。
10.(1)
质量/千克 0 5 10 15 20 25 30
总价/元 0 20 40 60 80 100 120
(2)大米的质量与总价成正比例关系;理由见详解
(3)4
【分析】(1)根据5千克总价20元,可以求出1千克的价钱,再乘25、乘30,求出的数再填表即可;根据画折线统计图的方法,把大米的质量与总价所对应的点在图中描出来,再连线即可;
(2)判断两种相关的量成什么比例,就看这两种量是比值一定还剩乘积一定;如果比值一定,成正比例,如果乘积一定,成反比例,判断出大米质量与总价成的比例;
(3)根据大米与总价成的比例,即可求出张阿姨买的大米的质量与李阿姨买的成什么比例,据此解答。
【详解】(1)20÷5=4(元)
25×4=100(元)
30×4=120(元)
质量/千克 0 5 10 15 20 25 30
总价/元 0 20 40 60 80 100 120
(2)5∶20=10∶40=15∶60=20∶80=25∶100=30∶120=(一定)
大米的质量与总价的比值一定,大米的质量与总价成正比例;
(3)大米的质量与总价成正比例,大米的质量与总价的比值一定,所以张阿姨买这种大米的总价是李阿姨的4倍,张阿姨买的大米的质量也应该是李阿姨的4倍。
【点睛】本题主要考查了统计图表的综合应用及正比例的应用,关键根据统计表中的数据完成统计图并解答问题。
11.3000克
【分析】10千克=10000克;每克甘蔗榨出的甘蔗汁的克数一定,即甘蔗汁的质量∶甘蔗的质量的比值一定,则甘蔗汁的质量与甘蔗的质量成正比例关系,设可以榨出x克甘蔗汁,列比例:150∶500=x∶10000,解比例,即可解答。
【详解】10千克=10000克
解:设可以榨出x克甘蔗汁。
150∶500=x∶10000
500x=150×10000
500x=1500000
x=1500000÷500
x=3000
答:可知榨出3000克甘蔗汁。
【点睛】关键是判断题目中的两种相关联的量成什么比例关系,据此列出相应的比例方程。
12.12次
【分析】因为每次运的根数×运的次数=总根数(一定),所以每次运的根数和运的次数成反比例,据此列比例解答即可。
【详解】解:设x次可以运完。
75x=60×15
75x=900
x=12
答:12次可以运完。
【点睛】此题主要考查用比例知识解答问题,关键要弄清哪个量一定,其它两种量成什么比例,再列出比例式解答。
13.(1)成正比例;理由见解析
(2)25;30;作图见解析
(3)60;21
【分析】(1)成正比例的两个相关联的量比值一定。
(2)根据表前面的数量关系,可得5、6人的船费。先从列中找人数,再从行中找对应的数量高度,点点顺次连线。
(3)根据单价×数量=总价,总价÷单价=数量,代入数据解答即可。
【详解】(1)这条船的乘船人数与所付船费成正比例,因为,是定值,所以这条船的乘船人数与所付船费是成正比例。
(2)5×5=25(元)
5×6=30(元)
作图如下:
(3)5×12=60(元)
105÷5=21(人)
所以,这条船乘坐了12人,那么所付船费是60元;付105元船费可乘坐21人。
【点睛】本题考查了学生的动手操作能力,及从统计图中获取信息的意识。
14.(1)成反比例,理由:每天烧煤的质量乘可烧的时间的积是一定的,所以每天烧煤的质量和可烧的时间成反比例。
(2)18天
【分析】(1)根据每天烧煤的质量和可烧的时间的乘积,结合反比例的意义判断。
(2)用这批煤的总质量除以每天烧煤的质量就是烧的天数。
【详解】(1)3×30=6×15=9×10=15×6=20×4.5=90(一定)
每天烧煤的质量和可烧的时间的乘积一定,所以每天烧煤的质量和可烧的时间成反比例。
(2)30×3÷5
=90÷5
=18(天)
答:这批煤可烧18天。
【点睛】本题考查了成反比例关系的判定及根据成反比例关系解决问题,关键是对题目中数量关系的分析。
15.(1)加工玩具的数量与时间成正比例关系,因为加工玩具的数量与时间这两个量的比值一定。
(2)见详解
(3)9;78
【分析】(1)两种相关联的量,如果两种量对应的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
(2)根据表格中的数据描点,连线即可。
(3)加工玩具的数量与时间成正比例,用108除以加工一个玩具的时间即可;用1小时加工的玩具个数乘6.5即可。
【详解】(1)据表分析加工玩具的数量与时间两个量之间的关系:
12∶1=24∶2=36∶3=48∶4=60∶5=12(一定),比值一定,所以加工玩具的数量与时间成正比例关系。
(2)如图:
(3)108÷12=9(小时)
12×6.5=78(个)
【点睛】本题考查了正比例的意义以及应用,同时还考查了对统计图的理解和掌握,并且要求能够根据统计图提供的信息,解决有关问题。
16.(1)订阅《少年报》的数量与总价成正比例关系。因为,比值是定值,所以订阅《少年报》的数量与总价成正比例。
(2)见详解;
(3)516;39
【分析】(1)因为:总价÷订阅数量=单价(一定),所以订阅《少年报》的数量与总价成正比例;
(2)根据数据,找出各点,然后把点依次连接即可;
(3)根据“单价×数量=总价”“数量=总价÷单价”进行解答。
【详解】(1)订阅《少年报》的数量与总价成正比例关系。
因为,比值是定值,所以订阅《少年报》的数量与总价成正比例关系。
(2)如下图
(3)12×43=516(元)
468÷12=39(份)
该校六(1)班要订阅43份《少年报》,一共需要516元;六(2)班订阅《少年报》一共花了468元,六(2)班订阅了39份《少年报》。
【点睛】此题考查了判断成正比例的量与成反比例量的方法及根据数据画出正比例图象,应注意知识的灵活运用。
17.(1)见详解
(2)成反比例,因为每箱装的个数乘装的箱数的积是一个定值
(3)32个
【分析】(1)先用每箱装的个数乘装的箱数等于苹果的总数,再用苹果的总数除以每箱装的个数,求出装的箱数;
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(3)用苹果的总个数除以装的箱数,即可求平均每箱装了多少个。
【详解】(1)如下表:
每箱装的个数 12 20 30 40 50
装的箱数 200 120 80 60 48
(2)因为2400(一定),根据两个相关联的量,如果它们乘积一定,就成反比例,所以箱装的个数和装的箱数成反比例。
(3)12×200÷75
=2400÷75
=32(个)
答:平均每箱装了32个。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
18.(1)反比例;(2)12辆
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例;由题可知,每辆汽车的载质量与所需汽车的数量的乘积一定,即建筑材料的总质量一定,是120吨;据此解答。
(2)由(1)可知,用建筑材料的总质量除以一辆汽车运输的吨数,即可求出需要汽车的量数。
【详解】(1)因为2.5×48=4×30=5×24=8×15=120(一定),所以每辆汽车的载质量与所需汽车数量成反比例关系。
(2)2.5×48÷10
=120÷10
=12(辆)
答:需要12辆汽车来运。
【点睛】本题主要考查反比例的辨识与实际应用,解题的关键是明确每辆汽车的载质量与所需汽车的数量之间的关系,进而解答。
19.(1)见详解
(2)正比例;原因见详解
(3)16小时
【分析】(1)根据统计表提供的数据,绘制统计图;
(2)断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例,据此解答。
(3)根据统计表,先求出碾米1吨需要的时间,即可求出碾米8吨需要的时间。
【详解】(1)
(2)0.5∶1=1∶2=1.5∶3=2∶4=2.5∶5=0.5(一定)
加工数量∶加工时间=每小时加工的数量(一定);工作时间和加工数量成正比例;
(3)8÷(0.5÷1)
=8÷0.5
=16(小时)
答:需要16小时。
【点睛】本题考查正比例意义和辨识,反比例意义和辨识;以及正比例的应用。
20.450块
【分析】移动营业大厅的面积是不变的,每一块方砖的面积与所需块数的乘积是一定的,即每一块方砖的面积×所需块数=移动营业大厅面积(一定),也就是两种相关联的量成反比例,由此设出未知数,列出比例式解答即可。
【详解】解:设需要用x块。
4×4×x=6×6×200
16x=7200
x=7200÷16
x=450
答:需要450块。
【点睛】此题首先利用正反比例的意义判定两种量的关系,再列比例式解答。注意:列比例式时不要把边长当成面积。
21.(1)成正比例;理由见解析
(2)300;350;画图见解析
(3)160;375
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例;这种丝绸面料购买的长度与金额的比值一定,即每米的价格是50元,所以这种丝绸面料购买的长度与金额是成正比例。据此解答。
(2)由(1)可知,这种丝绸面料每米的价格是50元,代入数据计算即可求出6米、7米的价格;横轴表示丝绸面料的长度,纵轴表示金额,根据统计表中的数据,依次进行描点,最后将各点顺次连接起来即可。
(3)根据“丝绸面料的长度×50=金额”,代入数据解答即可。
【详解】(1)这种丝绸面料购买的长度与金额成正比例,
因为,是定值,所以这种丝绸面料购买的长度与金额是成正比例。
(2)6×50=300(元)
7×50=350(元)
表格如下。
长度/米 0 1 2 3 4 5 6 7
金额/元 0 50 100 150 200 250 300 350
画图如下:
(3)8000÷50=160(米)
7.5×50=375(元)
答:8000元可以买160米这种丝绸面料;购买7.5米这种丝绸面需要375元。
【点睛】本题主要考查正比例的辨识、图像以及实际应用,解题的关键是明确丝绸面料购买的长度与金额成正比例,进而根据具体数据进行解答。
22.(1)见详解
(2)正
(3)17.5
【分析】(1)根据表格中的数据描点、连线即可;
(2)两种相关联的量,若其比值一定,两种量成正比例;若其乘积一定,两种量成反比例,再根据生产速度=产量÷生产时间,进行判断即可;
(3)由生产速度=产量÷生产时间,可以求出这台榨油机的生产速度,再用70吨的产量除以生产速度,即可算所需要的生产时间。
【详解】(1)如图:
(2)因为4∶1=8∶2=12∶3=16∶4=20∶5=24∶6=28∶7=4,可知产量与生产时间的比值一定,所以二者成正比例。
(3)榨油机生产速度为:
4÷1=4(吨/时)
70吨油需要时间:
70÷4=17.5(时)
【点睛】本题考查正比例图像的画法、正比例关系的判断以及利用正比例关系解决问题。
23.10天
【分析】根据题意可知,总工作量一定,工作时间和工作效率成反比例,由此用比例解答即可。
【详解】解:设可以提前x天完成。
(40+8)×(60-x)=40×60
48×(60-x)=2400
48×(60-x)÷48=2400÷48
60-x=50
x=10
答:实际提前10天完成。
【点睛】此题解题的关键,弄清题意,根据工作效率、工作时间和工作量三者之间的关系,判断哪两种量成何比例,然后找出对应量,列式解答即可。
24.50平方米
【分析】根据题意,每分钟喷洒的面积×喷洒的实际=小区公共区域的面积(一定),因为小区公共区域的面积是一个定值,所以每分钟喷洒的面积与喷洒的时间成反比例,设每分钟应喷洒x平方米,列方程:28x=35×40,解方程,即可解答。
【详解】解:设每分钟应喷洒x平方米。
28x=35×40
28x=1400
x=1400÷28
x=50
答:每分钟应喷洒50平方米。
【点睛】解答本题的关键是先判断两个相关的量成什么比例,并找准对应量。
25.(1)16;20
(2)正比例;理由见详解
(3)见详解
(4)48;17
【分析】(1)根据表中数据可知,1支钢笔4元,2支钢笔8元,3支钢笔12元,根据公式:总价=单价×数量,代入数据即可填表;
(2)判断成什么比例,就看两个相关联的量是比值一定,还是乘积一定,比值一定成正比例,乘积一定,成反比例,据此判断;
(3)根据表中数据,在图中描点,连线;
(4)根据总计=单价×数量;数量=总价÷单价,代入数据,即可解答。
【详解】(1)4×4=16(元);4×5=20(元)
数量/支 0 1 2 3 4 5
总价/元 0 4 8 12 16 20
(2)4∶1=8∶2=12∶3=16∶4=4(一定)总价与数量的比值一定;购买圆珠笔的数量与总价成正比例。
(3)
(4)4×12=48(元)
70÷4=17(支)……2(元)
【点睛】本题考查了正比例关系的辨识,正比例图形的画法,以及利用正比例解答问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版小学数学六年级下册
第四单元《正比例与反比例》单元专项训练——应用题
1.在比例尺为1∶10000000的地图上,量得甲地到乙地的高速铁路长6.6厘米。高速铁路上的火车平均运行速度为210千米/时,从甲地到乙地乘火车大约需几小时?(得数保留一位小数)
2.用一些纸装订同样的练习本,每本用纸的张数和装订的本数如下表。
每本用纸张数/张 8 10 15 20 24
装订本数/本 75 60 40
(1)将上表补充完整。
(2)每本用纸张数和装订本数是不是成反比例?说明理由。
(3)如果用这些纸装订成50本练习本(每本用纸张数相同),每本用纸多少张?
3.购买一种笔筒的数量和应付金额如下表。
数量/个 0 1 2 3 4 5 …
应付金额/元业 0 8 16 24 32 40 …
(1)判断应付金额与笔筒的数量是否成正比例关系,并说明理由。
(2)先把上表中数量和应付金额所对应的点描在方格纸上,再顺次连接。
(3)买20个笔筒需要( )元,144元最多可以买( )个这样的笔筒。
4.某环保节能造纸厂造纸总量与所用时间如下表。
时间/天 0 1 2 3 4 5 …
生产总量/吨 0 12 24 36 48 60 …
(1)生产总量和时间成正比例关系吗?说明理由。
(2)在下图中描出时间与生产总量对应的点,再顺次连接。
(3)8天可以生产( )吨纸,生产90吨纸需要( )天。
5.学校买来一批打印纸,计划每天用200张,可用45天,实际节约用纸后,每天少用了50张,实际这些打印纸多用了多少天?
6.甲、乙两地相距520千米。一辆汽车从甲地开往乙地,4时行驶了160千米。照这样的速度,这辆汽车从甲地到乙地需要开几小时?(用比例解)
7.造纸术是中国四大发明之一,是中华民族对世界文明的巨大贡献,是人类文明史上的一项杰出的发明创造。某造纸厂的生产情况如下表,根据表回答问题。
时间(天) 0 1 2 3 4 5 6 7 …
生产量(吨) 0 70 140 210 280 350 420 490 …
(1)生产量和所用时间成正比例关系吗?为什么?
(2)根据表中的数据,写出一个比例( )。
(3)在下图中描出表示时间和相应生产量对应的点,并把它们按顺序连接起来。
(4)生产560吨纸需要( )天。
8.磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 0 1 2 3 4 5 6 …
路程/千米 0 7 14 21 28 35 42 …
(1)图中的点A表示时间为1分时,磁悬浮列车行驶过的路程为7千米。请你试着描出其他各点并顺次连接。
(2)列车运行4.5分时,行驶的路程是多少?
9.输液时,一小瓶葡萄糖液均匀滴落,每分滴数与所需时间的关系如下。
每分滴数/滴 30 40 50 60 …
时间/分 40 30 …
(1)请把上表补充完整。
(2)每分滴数与所需时间这两个量是否成正比例或反比例?为什么?
10.下面是某超市一种大米的质量和总价的统计表。
质量/千克 0 5 10 15 20 25 30
总价/元 0 20 40 60 80
(1)先把上表填写完整,再把大米的质量与总价所对应的点在下图中描出来,并连线。
(2)大米的质量与总价成正比例关系吗?为什么?
(3)张阿姨买这种大米的总价是李阿姨的4倍,张阿姨买的大米的质量是李阿姨的( )倍。
11.有一个甘蔗榨汁机,可以用500克的甘蔗榨出150克的甘蔗汁,现在有10千克的甘蔗,可以榨出多少克甘蔗汁?(用比例解答)
12.一辆卡车运一堆木材,如果每次运60根,15次刚好可以运完;如果每次运75根,多少次可完?(用比例知识解答)
13.某条船的乘船人数与所付船费如下表。
乘船人数/人 0 1 2 3 4 5 6 …
所付船费/元 0 5 10 15 20 …
(1)判断这条船的乘船人数与所付船费是不是成正比例,并说明理由。
(2)先将上面的表格填写完整,再根据表中数据,在下图中描出这条船的乘船人数与所付船费所对应的点,再把这些点依次连接起来。
(3)如果这条船乘坐了12人,那么所付船费是( )元;付105元船费可乘坐( )人。
14.某工厂有一批煤,每天烧煤的质量和可烧的时间关系如下表。
每天烧煤的质量/吨 0 3 6 9 15 20 …
可烧的时间/天 0 30 15 10 6 4.5 …
(1)判断每天烧煤的质量和可烧的时间是不是成反比例,并说明理由。
(2)如果该工厂平均每天烧煤的质量是5吨,那么这批煤可烧多少天?
15.张师傅加工一批玩具时,加工时间与数量的变化情况如下表。
加工时间/时 0 1 2 3 4 5 …
加工数量/个 0 12 24 36 48 60 …
(1)加工玩具的数量与时间成正比例关系吗?为什么?
(2)根据表中数据,在下图,再把这些点依次连起来。
(3)加工108个玩具需要( )小时,6.5小时可以加工( )个玩具。
16.下面是某小学六(3)班订阅《少年报》的数量与总价的对应数值表。
数量/份 0 1 2 3 4 5 6 ……
总价/元 0 12 24 36 48 60 72 ……
(1)订阅《少年报》的数量与总价成正比例关系吗?为什么?
(2)在下图中描出该小学六(3)班订阅《少年报》的数量与总价的点,然后把它们按顺序连起来。
(3)该校六(1)班要订阅43份《少年报》,一共需要( )元;六(2)班订阅《少年报》一共花了468元,六(2)班订阅了( )份《少年报》。
17.李叔叔摘了一些苹果,每箱装的个数和装的箱数如下表。
每箱装的个数 12 20 30 40 50
装的箱数 200 120 80
(1)完成上表。
(2)每箱装的个数和装的箱数成反比例吗?为什么?
(3)如果装了75箱,平均每箱装了多少个?
18.某运输公司要将一批建筑材料一次运往建筑工地。每辆汽车的载质量与所需汽车的数量如下表。
每辆汽车的载质量/吨 2.5 4 5 8
所需汽车数量/辆 48 30 24 15
(1)每辆汽车的载质量与所需汽车数量成什么比例关系?
(2)如果这批建筑材料用载质量为10吨的汽车一次运完。需要多少辆汽车来运?
19.一台碾米机碾米情况如下表:
工作时间(时) 0 1 2 3 4 5
加工数量(吨) 0 0.5 1 1.5 2 2.5
(1)把上表中相对应的点描在下图中,再顺次连接。
(2)工作时间与加工数量成什么比例?为什么?
(3)现在碾米8吨,需要几小时?
20.某移动营业大厅,用边长为6分米的方砖铺地,需用200块;若改铺边长为4分米的方砖铺,需要多少块?
21.一种丝绸面料购买的长度与金额的情况如下表。
长度/米 0 1 2 3 4 5 6 7
金额/元 0 50 100 150 200 250
(1)判断这种丝绸面料购买的长度与金额是不是成正比例,并说明理由。
(2)先将上面的表格填写完整,再根据表中数据,在下图中描出这种丝绸面料购买的长度与金额所对应的点,再把这些点依次连接起来。
(3)8000元可以买( )米这种丝绸面料;购买7.5米这种丝绸面需要( )元。
22.某台榨油机的生产时间与产量的关系如下表。
生产时间/时 0 1 2 3 4 5 6 7
产量/吨 0 4 8 12 16 20 24 28
(1)先根据上表描点,再顺次连接各点。
(2)生产时间与产量成( )(填“正”或“反”)比例关系。
(3)这台榨油机榨70吨油需要( )时。
23.某工厂生产一批笔记本电脑,原计划每天生产40台,60天完成。实际每天多生产8台,实际提前多少天完成?(用比例解答)
24.根据疫情防控要求,王师傅用喷雾器对小区的公共区域进行全覆盖消毒。如果每分钟喷洒35平方米,40分钟能全部消杀一遍,现在想用28分钟完成任务,每分钟应喷洒多少平方米?(用比例知识解答)
25.晶晶去文具店购买同一支圆珠笔,购买圆珠笔的数量和总价如下表所示。
数量/支 0 1 2 3 4 5
总价/元 0 4 8 12
(1)把上表填写完整。
(2)购买圆珠笔的数量与总价成正比例吗?为什么?
(3)先根据上表描点,再顺次连接各点。
晶晶想要买12支这种圆珠笔,一共需要花费( )元;如果晶晶有70元,她最多可以买( )支这种圆珠笔。
参考答案:
1.3.1小时
【分析】已知比例尺和甲地到乙地高速铁路的图上距离,根据“实际距离=图上距离÷比例尺”,求出甲地到乙地高速铁路的实际距离,并根据进率“1千米=100000厘米”换算;然后根据“时间=路程÷速度”,求出从甲地到乙地乘火车需要的时间。
【详解】6.6÷
=6.6×10000000
=66000000(厘米)
66000000厘米=660千米
660÷210≈3.1(小时)
答:从甲地到乙地乘火车大约需3.1小时。
【点睛】本题考查比例尺的应用以及行程问题,掌握图上距离、实际距离、比例尺之间的关系,以及速度、时间、路程之间的关系是解题的关键。
2.(1)30;25
(2)成反比例;理由见详解
(3)12张
【分析】(1)8×75=10×60=15×40=600;根据积都是600,用600除以20和24即可;
(2)判断练习本每本的页数和装订的本数之间成什么比例,就看这两个量是对应的比值一定还是乘积一定;如果是比值一定,成正比例;如果是乘积一定,就成反比例;据此解答;
(3)用600除以50即可求出每本用纸多少张。
【详解】(1)8×75÷20
=600÷20
=30(本)
8×75÷24
=600÷24
=25(本)
每本用纸张数/张 8 10 15 20 24
装订本数/本 75 60 40 30 25
(2)因为8×75=10×60=15×40=20×30=24×25=600(一定)
乘积一定,所以每本用纸张数与装订本数成反比例。
(3)8×75÷50
=600÷50
=12(张)
答:每本用纸12张。
【点睛】利用正比例意义和辨识,反比例意义和辨识以及反比例的应用进行解答。
3.(1)应付金额与笔筒的数量成正比例关系,理由:应付金额与笔筒的数量的比值一定,所以应付金额与笔筒的数量成正比例关系。
(2)见详解
(3)160;18
【分析】(1)因为应付金额÷数量=单价(一定),所以应付金额与数量是成正比例关系。
(2)根据统计表中的数据描出各点,然后顺序连接各点即可。
(3)根据单价×数量=总价,总价÷单价=数量,据此列式解答。
【详解】(1)应付金额与笔筒的数量成正比例关系,理由如下:因为40∶5=32∶4=24∶3=16∶2=8∶1=8(定值),所以应付金额与笔筒的数量成正比例关系。
(2)如图:
(3)20×8=160(元)
144÷8=18(个)
买20个笔筒需要160元,144元最多可以买18个这样的笔筒。
【点睛】此题考查的目的是理解掌握正比例的意义及应用,明确:正比例的图像
4.(1)成正比例关系;理由见详解
(2)见详解
(3)96;7.5
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例;据此解答。
(2)首先根据统计表中的数据在图中描出各点,然后顺次连接各点即可。
(3)每天的生产效率×生产的天数=生产总量即可解答。
【详解】(1)生产总量和时间成正比例关系;因为12∶1=24∶2=36∶3=48∶4=60∶5=定值。所以生产总量和时间成正比例关系。
(2)作图如下:
(3)8×12=96(吨)
90÷12=7.5(天)
答:8天可以生产96吨纸,生产90吨纸需要7.5天。
【点睛】此题考查的意义是理解掌握正比例的意义及应用。
5.15天
【分析】根据题意,打印纸的总张数没有变化,找出等量关系:计划用的时间×计划每天用的张数=实际用的时间×实际每天用的张数,列方程解答。
【详解】解:设实际这些打印纸多用了x天。
(200-50)×(45+x)=200×45
150×(45+x)=9000
6750+150x=9000
150x=2250
x=15
答:实际这些打印纸多用了15天。
【点睛】本题考查有关计划与实际比较应用题的计算及应用,出数量关系,列式计算即可。
6.13小时
【分析】根据题意,速度一定,路程与时间成正比例,可得:甲、乙两地路程∶从甲地到乙地需要的时间=4小时行驶的路程∶4小时。
【详解】解:设这辆汽车从甲地到乙地需要开x小时。
520∶x=160∶4
160x=520×4
160x÷160=2080÷160
x=13
答:这辆汽车从甲地到乙地需要开13小时。
【点睛】根据速度不变列出比例,是解答此题的关键。
7.(1)成正比例关系;因为:======。
(2)1∶70=2∶140(答案不唯一)
(3)
(4)8
【分析】(1)根据生产量与生产时间的比的比值判断是不是成正比例;
(2)从表中找出两组数据,写成比例式;
(3)根据表中数据描点、连线;
(4)用560除以每天生产的吨数即可。
【详解】(1)======。
所以生产量和所用时间成正比例关系。
(2)1∶70=2∶140(答案不唯一)
(3)
(4)560÷70=8(天)
【点睛】本题考查了正比例关系的判断、写比例式、画正比例关系图像、根据正比例关系解决问题等,综合性强,需仔细更新和解答。
8.(1)见详解;
(2)31.5千米
【分析】将表中的数据进行分析,可知路程与时间的比值一定,即路程与时间成正比例关系;
(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米,可知本次列车的速度为7千米/分,依据表中数据将其他各点在图中描出即可;
(2) 列车运行4.5分时,依据路程=时间×速度,将数据代入即可行驶的路程。
【详解】(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米,依据表中数据将其他各点在图中描出。如下图:
(2)4.5×7=31.5(千米)
答:行驶的路程是31.5千米。
【点睛】本题主要考查了正比例关系的应用,掌握成正比例的量的变化规律及其特征是解答此题的关键。
9.(1)24;20
(2)成反比例;理由见解析。
【分析】(1)观察统计表可知,一小瓶葡萄糖液的滴数是一定的,即总滴数=每分钟滴的滴数×滴的时间;根据表中每分钟滴30滴、40滴时所用的时间,皆可求出一小瓶葡萄糖液的总滴数,据此即可求出每分钟滴50滴、60滴的所用时间。
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此解答。
【详解】由分析可知:
(1)30×40=1200(滴)
1200÷50=24(分)
1200÷60=20(分)
(2)成反比例,因为30×40=40×30=1200(一定),每分滴数与所需时间的乘积一定,所以每分滴数与所需时间这两个量成反比例。
【点睛】本题主要考查反比例的辨识及实际应用,通过统计表获取信息的意识。
10.(1)
质量/千克 0 5 10 15 20 25 30
总价/元 0 20 40 60 80 100 120
(2)大米的质量与总价成正比例关系;理由见详解
(3)4
【分析】(1)根据5千克总价20元,可以求出1千克的价钱,再乘25、乘30,求出的数再填表即可;根据画折线统计图的方法,把大米的质量与总价所对应的点在图中描出来,再连线即可;
(2)判断两种相关的量成什么比例,就看这两种量是比值一定还剩乘积一定;如果比值一定,成正比例,如果乘积一定,成反比例,判断出大米质量与总价成的比例;
(3)根据大米与总价成的比例,即可求出张阿姨买的大米的质量与李阿姨买的成什么比例,据此解答。
【详解】(1)20÷5=4(元)
25×4=100(元)
30×4=120(元)
质量/千克 0 5 10 15 20 25 30
总价/元 0 20 40 60 80 100 120
(2)5∶20=10∶40=15∶60=20∶80=25∶100=30∶120=(一定)
大米的质量与总价的比值一定,大米的质量与总价成正比例;
(3)大米的质量与总价成正比例,大米的质量与总价的比值一定,所以张阿姨买这种大米的总价是李阿姨的4倍,张阿姨买的大米的质量也应该是李阿姨的4倍。
【点睛】本题主要考查了统计图表的综合应用及正比例的应用,关键根据统计表中的数据完成统计图并解答问题。
11.3000克
【分析】10千克=10000克;每克甘蔗榨出的甘蔗汁的克数一定,即甘蔗汁的质量∶甘蔗的质量的比值一定,则甘蔗汁的质量与甘蔗的质量成正比例关系,设可以榨出x克甘蔗汁,列比例:150∶500=x∶10000,解比例,即可解答。
【详解】10千克=10000克
解:设可以榨出x克甘蔗汁。
150∶500=x∶10000
500x=150×10000
500x=1500000
x=1500000÷500
x=3000
答:可知榨出3000克甘蔗汁。
【点睛】关键是判断题目中的两种相关联的量成什么比例关系,据此列出相应的比例方程。
12.12次
【分析】因为每次运的根数×运的次数=总根数(一定),所以每次运的根数和运的次数成反比例,据此列比例解答即可。
【详解】解:设x次可以运完。
75x=60×15
75x=900
x=12
答:12次可以运完。
【点睛】此题主要考查用比例知识解答问题,关键要弄清哪个量一定,其它两种量成什么比例,再列出比例式解答。
13.(1)成正比例;理由见解析
(2)25;30;作图见解析
(3)60;21
【分析】(1)成正比例的两个相关联的量比值一定。
(2)根据表前面的数量关系,可得5、6人的船费。先从列中找人数,再从行中找对应的数量高度,点点顺次连线。
(3)根据单价×数量=总价,总价÷单价=数量,代入数据解答即可。
【详解】(1)这条船的乘船人数与所付船费成正比例,因为,是定值,所以这条船的乘船人数与所付船费是成正比例。
(2)5×5=25(元)
5×6=30(元)
作图如下:
(3)5×12=60(元)
105÷5=21(人)
所以,这条船乘坐了12人,那么所付船费是60元;付105元船费可乘坐21人。
【点睛】本题考查了学生的动手操作能力,及从统计图中获取信息的意识。
14.(1)成反比例,理由:每天烧煤的质量乘可烧的时间的积是一定的,所以每天烧煤的质量和可烧的时间成反比例。
(2)18天
【分析】(1)根据每天烧煤的质量和可烧的时间的乘积,结合反比例的意义判断。
(2)用这批煤的总质量除以每天烧煤的质量就是烧的天数。
【详解】(1)3×30=6×15=9×10=15×6=20×4.5=90(一定)
每天烧煤的质量和可烧的时间的乘积一定,所以每天烧煤的质量和可烧的时间成反比例。
(2)30×3÷5
=90÷5
=18(天)
答:这批煤可烧18天。
【点睛】本题考查了成反比例关系的判定及根据成反比例关系解决问题,关键是对题目中数量关系的分析。
15.(1)加工玩具的数量与时间成正比例关系,因为加工玩具的数量与时间这两个量的比值一定。
(2)见详解
(3)9;78
【分析】(1)两种相关联的量,如果两种量对应的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
(2)根据表格中的数据描点,连线即可。
(3)加工玩具的数量与时间成正比例,用108除以加工一个玩具的时间即可;用1小时加工的玩具个数乘6.5即可。
【详解】(1)据表分析加工玩具的数量与时间两个量之间的关系:
12∶1=24∶2=36∶3=48∶4=60∶5=12(一定),比值一定,所以加工玩具的数量与时间成正比例关系。
(2)如图:
(3)108÷12=9(小时)
12×6.5=78(个)
【点睛】本题考查了正比例的意义以及应用,同时还考查了对统计图的理解和掌握,并且要求能够根据统计图提供的信息,解决有关问题。
16.(1)订阅《少年报》的数量与总价成正比例关系。因为,比值是定值,所以订阅《少年报》的数量与总价成正比例。
(2)见详解;
(3)516;39
【分析】(1)因为:总价÷订阅数量=单价(一定),所以订阅《少年报》的数量与总价成正比例;
(2)根据数据,找出各点,然后把点依次连接即可;
(3)根据“单价×数量=总价”“数量=总价÷单价”进行解答。
【详解】(1)订阅《少年报》的数量与总价成正比例关系。
因为,比值是定值,所以订阅《少年报》的数量与总价成正比例关系。
(2)如下图
(3)12×43=516(元)
468÷12=39(份)
该校六(1)班要订阅43份《少年报》,一共需要516元;六(2)班订阅《少年报》一共花了468元,六(2)班订阅了39份《少年报》。
【点睛】此题考查了判断成正比例的量与成反比例量的方法及根据数据画出正比例图象,应注意知识的灵活运用。
17.(1)见详解
(2)成反比例,因为每箱装的个数乘装的箱数的积是一个定值
(3)32个
【分析】(1)先用每箱装的个数乘装的箱数等于苹果的总数,再用苹果的总数除以每箱装的个数,求出装的箱数;
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(3)用苹果的总个数除以装的箱数,即可求平均每箱装了多少个。
【详解】(1)如下表:
每箱装的个数 12 20 30 40 50
装的箱数 200 120 80 60 48
(2)因为2400(一定),根据两个相关联的量,如果它们乘积一定,就成反比例,所以箱装的个数和装的箱数成反比例。
(3)12×200÷75
=2400÷75
=32(个)
答:平均每箱装了32个。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
18.(1)反比例;(2)12辆
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例;由题可知,每辆汽车的载质量与所需汽车的数量的乘积一定,即建筑材料的总质量一定,是120吨;据此解答。
(2)由(1)可知,用建筑材料的总质量除以一辆汽车运输的吨数,即可求出需要汽车的量数。
【详解】(1)因为2.5×48=4×30=5×24=8×15=120(一定),所以每辆汽车的载质量与所需汽车数量成反比例关系。
(2)2.5×48÷10
=120÷10
=12(辆)
答:需要12辆汽车来运。
【点睛】本题主要考查反比例的辨识与实际应用,解题的关键是明确每辆汽车的载质量与所需汽车的数量之间的关系,进而解答。
19.(1)见详解
(2)正比例;原因见详解
(3)16小时
【分析】(1)根据统计表提供的数据,绘制统计图;
(2)断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例,据此解答。
(3)根据统计表,先求出碾米1吨需要的时间,即可求出碾米8吨需要的时间。
【详解】(1)
(2)0.5∶1=1∶2=1.5∶3=2∶4=2.5∶5=0.5(一定)
加工数量∶加工时间=每小时加工的数量(一定);工作时间和加工数量成正比例;
(3)8÷(0.5÷1)
=8÷0.5
=16(小时)
答:需要16小时。
【点睛】本题考查正比例意义和辨识,反比例意义和辨识;以及正比例的应用。
20.450块
【分析】移动营业大厅的面积是不变的,每一块方砖的面积与所需块数的乘积是一定的,即每一块方砖的面积×所需块数=移动营业大厅面积(一定),也就是两种相关联的量成反比例,由此设出未知数,列出比例式解答即可。
【详解】解:设需要用x块。
4×4×x=6×6×200
16x=7200
x=7200÷16
x=450
答:需要450块。
【点睛】此题首先利用正反比例的意义判定两种量的关系,再列比例式解答。注意:列比例式时不要把边长当成面积。
21.(1)成正比例;理由见解析
(2)300;350;画图见解析
(3)160;375
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例;这种丝绸面料购买的长度与金额的比值一定,即每米的价格是50元,所以这种丝绸面料购买的长度与金额是成正比例。据此解答。
(2)由(1)可知,这种丝绸面料每米的价格是50元,代入数据计算即可求出6米、7米的价格;横轴表示丝绸面料的长度,纵轴表示金额,根据统计表中的数据,依次进行描点,最后将各点顺次连接起来即可。
(3)根据“丝绸面料的长度×50=金额”,代入数据解答即可。
【详解】(1)这种丝绸面料购买的长度与金额成正比例,
因为,是定值,所以这种丝绸面料购买的长度与金额是成正比例。
(2)6×50=300(元)
7×50=350(元)
表格如下。
长度/米 0 1 2 3 4 5 6 7
金额/元 0 50 100 150 200 250 300 350
画图如下:
(3)8000÷50=160(米)
7.5×50=375(元)
答:8000元可以买160米这种丝绸面料;购买7.5米这种丝绸面需要375元。
【点睛】本题主要考查正比例的辨识、图像以及实际应用,解题的关键是明确丝绸面料购买的长度与金额成正比例,进而根据具体数据进行解答。
22.(1)见详解
(2)正
(3)17.5
【分析】(1)根据表格中的数据描点、连线即可;
(2)两种相关联的量,若其比值一定,两种量成正比例;若其乘积一定,两种量成反比例,再根据生产速度=产量÷生产时间,进行判断即可;
(3)由生产速度=产量÷生产时间,可以求出这台榨油机的生产速度,再用70吨的产量除以生产速度,即可算所需要的生产时间。
【详解】(1)如图:
(2)因为4∶1=8∶2=12∶3=16∶4=20∶5=24∶6=28∶7=4,可知产量与生产时间的比值一定,所以二者成正比例。
(3)榨油机生产速度为:
4÷1=4(吨/时)
70吨油需要时间:
70÷4=17.5(时)
【点睛】本题考查正比例图像的画法、正比例关系的判断以及利用正比例关系解决问题。
23.10天
【分析】根据题意可知,总工作量一定,工作时间和工作效率成反比例,由此用比例解答即可。
【详解】解:设可以提前x天完成。
(40+8)×(60-x)=40×60
48×(60-x)=2400
48×(60-x)÷48=2400÷48
60-x=50
x=10
答:实际提前10天完成。
【点睛】此题解题的关键,弄清题意,根据工作效率、工作时间和工作量三者之间的关系,判断哪两种量成何比例,然后找出对应量,列式解答即可。
24.50平方米
【分析】根据题意,每分钟喷洒的面积×喷洒的实际=小区公共区域的面积(一定),因为小区公共区域的面积是一个定值,所以每分钟喷洒的面积与喷洒的时间成反比例,设每分钟应喷洒x平方米,列方程:28x=35×40,解方程,即可解答。
【详解】解:设每分钟应喷洒x平方米。
28x=35×40
28x=1400
x=1400÷28
x=50
答:每分钟应喷洒50平方米。
【点睛】解答本题的关键是先判断两个相关的量成什么比例,并找准对应量。
25.(1)16;20
(2)正比例;理由见详解
(3)见详解
(4)48;17
【分析】(1)根据表中数据可知,1支钢笔4元,2支钢笔8元,3支钢笔12元,根据公式:总价=单价×数量,代入数据即可填表;
(2)判断成什么比例,就看两个相关联的量是比值一定,还是乘积一定,比值一定成正比例,乘积一定,成反比例,据此判断;
(3)根据表中数据,在图中描点,连线;
(4)根据总计=单价×数量;数量=总价÷单价,代入数据,即可解答。
【详解】(1)4×4=16(元);4×5=20(元)
数量/支 0 1 2 3 4 5
总价/元 0 4 8 12 16 20
(2)4∶1=8∶2=12∶3=16∶4=4(一定)总价与数量的比值一定;购买圆珠笔的数量与总价成正比例。
(3)
(4)4×12=48(元)
70÷4=17(支)……2(元)
【点睛】本题考查了正比例关系的辨识,正比例图形的画法,以及利用正比例解答问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
