5.2运动的合成与分解 课件 (共16张PPT)高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 5.2运动的合成与分解 课件 (共16张PPT)高一下学期物理人教版(2019)必修第二册 | 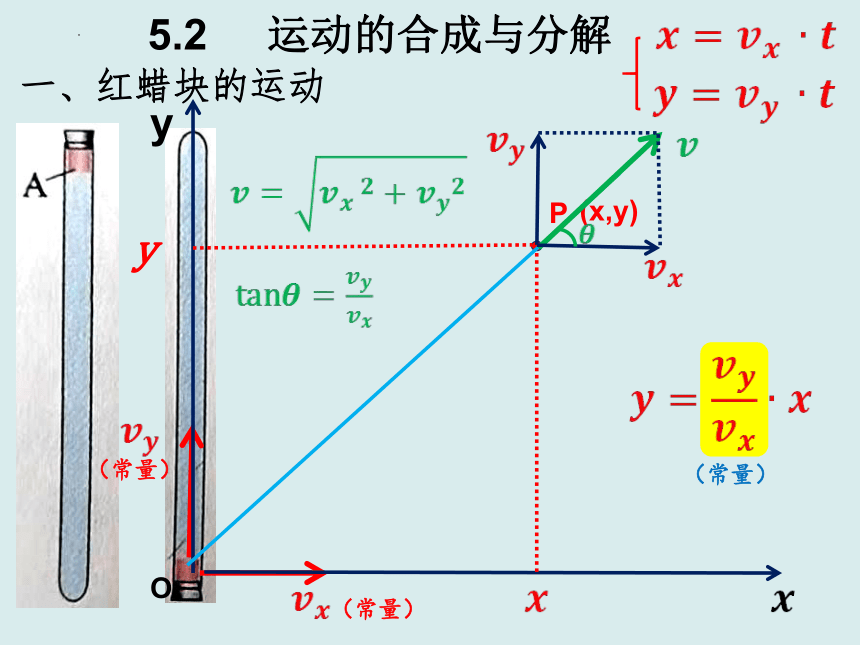 | |
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-10 12:58:12 | ||
图片预览


文档简介
(共16张PPT)
5.2 运动的合成与分解
一、红蜡块的运动
(常量)
(常量)
O
y
P
(x,y)
y
(常量)
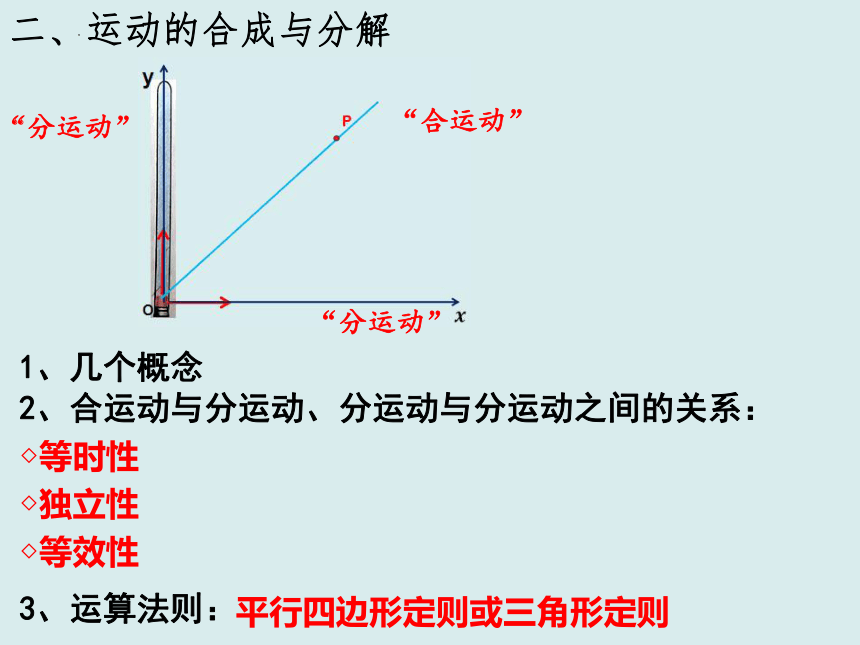
二、运动的合成与分解
“合运动”
“分运动”
“分运动”
1、几个概念
2、合运动与分运动、分运动与分运动之间的关系:
◇等时性
◇独立性
◇等效性
平行四边形定则或三角形定则
3、运算法则:
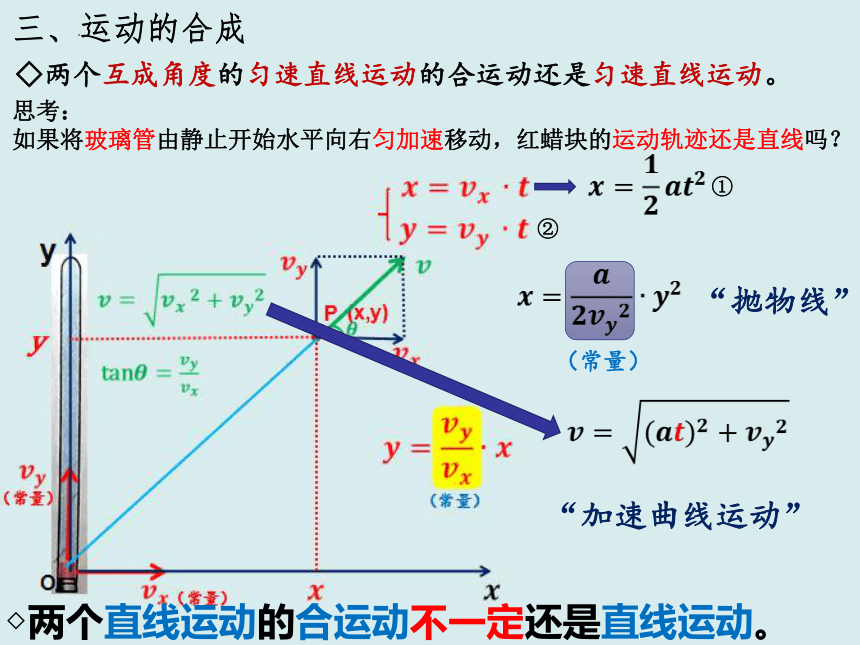
三、运动的合成
思考:
如果将玻璃管由静止开始水平向右匀加速移动,红蜡块的运动轨迹还是直线吗?
①
②
(常量)
“抛物线”
◇两个直线运动的合运动不一定还是直线运动。
“加速曲线运动”
◇两个互成角度的匀速直线运动的合运动还是匀速直线运动。
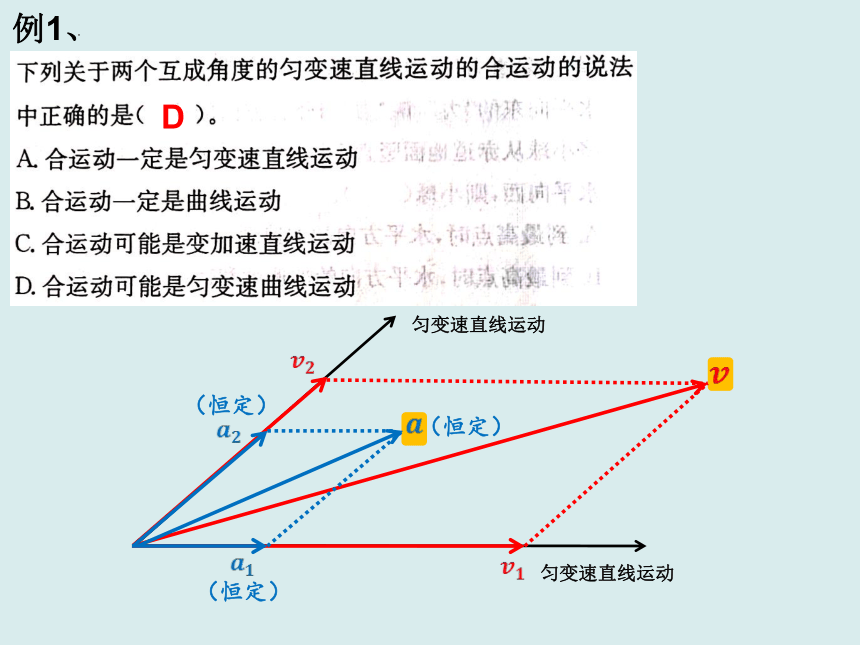
例1、
匀变速直线运动
匀变速直线运动
(恒定)
(恒定)
(恒定)
D
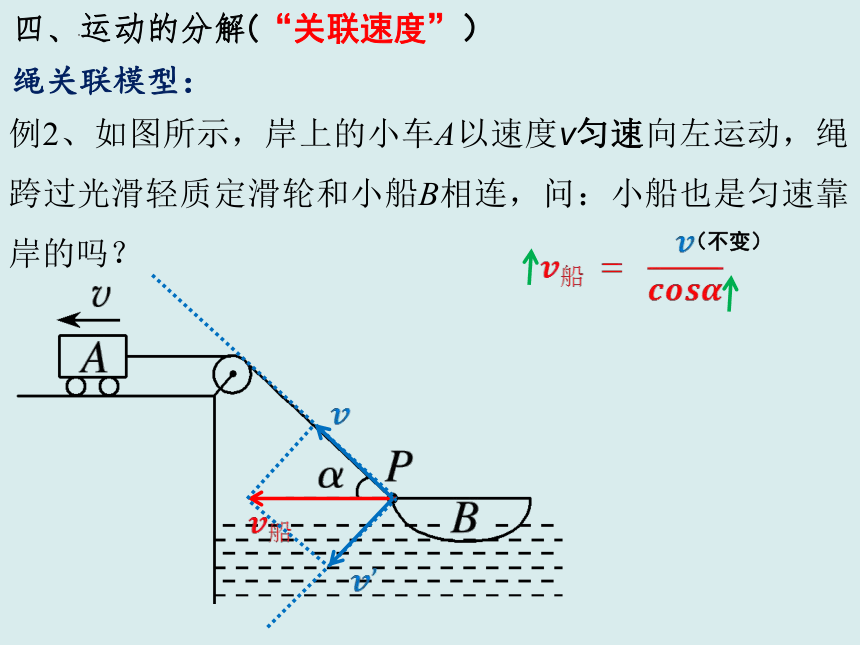
四、运动的分解
(“关联速度”)
例2、如图所示,岸上的小车A以速度v匀速向左运动,绳跨过光滑轻质定滑轮和小船B相连,问:小船也是匀速靠岸的吗?
绳关联模型:
(不变)
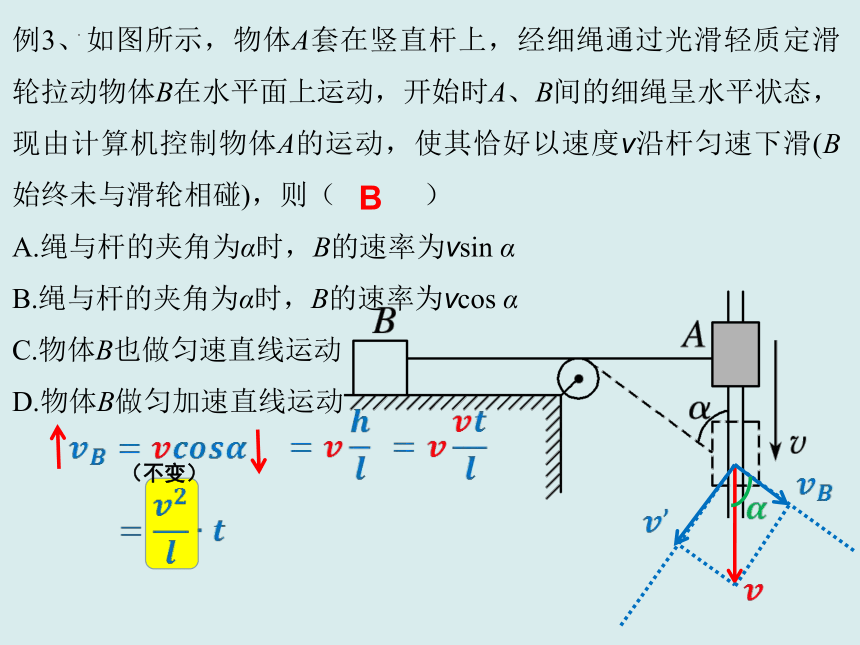
例3、如图所示,物体A套在竖直杆上,经细绳通过光滑轻质定滑轮拉动物体B在水平面上运动,开始时A、B间的细绳呈水平状态,现由计算机控制物体A的运动,使其恰好以速度v沿杆匀速下滑(B始终未与滑轮相碰),则( )
A.绳与杆的夹角为α时,B的速率为vsin α
B.绳与杆的夹角为α时,B的速率为vcos α
C.物体B也做匀速直线运动
D.物体B做匀加速直线运动
B
(不变)
例4、A、B两物体通过一根跨过光滑轻质定滑轮的轻绳相连放在水平面上,现物体A以v1的速度向右匀速运动,当绳被拉成与水平面夹角分别是α、β时,如图7所示,物体B的运动速度vB为(绳始终有拉力)( )
D
杆关联模型:
例5、如图所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动.当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面滑动的速度大小为v2,则v1、v2的关系是( )
A.v1=v2 B.v1=v2cos θ C.v1=v2tan θ D.v1=v2sin θ
C
【课后小结】
2、通过红蜡块的运动了解了合运动与分运动的概念以及
它们之间的关系。
1、如何建立平面直角坐标系去研究平面运动,以及如何
用轨迹方程去描述平面运动。
3、如何通过运动的合成从运动学的角度去研究合运动。
4、如何通过运动的分解去研究“关联速度”的问题。
专题:小船过河的问题
例:
练习1、如图所示,小船沿直线AB过河,船头始终垂直于河岸。若水流速度减小,为保持航线不变,下列措施与结论正确的是( )
A.减小船速,过河时间变长 B.减小船速,过河时间不变
C.增大船速,过河时间不变 D.增大船速,过河时间缩短
A
A
B
(不变)
思考:如果船速、水速恒定,
什么情况下渡河时间最短?
什么情况下渡河位移最短?
时间最短:
位移最短:
(一定)
A
B
C
练习2、
A
B
√
√
=2.5m/s
练习3.河水的流速随离河岸一侧的距离的变化关系如图甲所示,船在静水中的速度与时间的关系如图乙所示,若要使船以最短时间渡河,则( )
A.船渡河的最短时间是60 s
B.船在行驶过程中,船头始终与河岸垂直
C.船在河水中航行的轨迹是一条直线
D.船在河水中的最大速度是5 m/s
河宽
船速
√
√
【课后小结】
1、渡河时间最短:
垂直于河岸时
2、渡河位移最短:
垂直于河岸时
5.2 运动的合成与分解
一、红蜡块的运动
(常量)
(常量)
O
y
P
(x,y)
y
(常量)
二、运动的合成与分解
“合运动”
“分运动”
“分运动”
1、几个概念
2、合运动与分运动、分运动与分运动之间的关系:
◇等时性
◇独立性
◇等效性
平行四边形定则或三角形定则
3、运算法则:
三、运动的合成
思考:
如果将玻璃管由静止开始水平向右匀加速移动,红蜡块的运动轨迹还是直线吗?
①
②
(常量)
“抛物线”
◇两个直线运动的合运动不一定还是直线运动。
“加速曲线运动”
◇两个互成角度的匀速直线运动的合运动还是匀速直线运动。
例1、
匀变速直线运动
匀变速直线运动
(恒定)
(恒定)
(恒定)
D
四、运动的分解
(“关联速度”)
例2、如图所示,岸上的小车A以速度v匀速向左运动,绳跨过光滑轻质定滑轮和小船B相连,问:小船也是匀速靠岸的吗?
绳关联模型:
(不变)
例3、如图所示,物体A套在竖直杆上,经细绳通过光滑轻质定滑轮拉动物体B在水平面上运动,开始时A、B间的细绳呈水平状态,现由计算机控制物体A的运动,使其恰好以速度v沿杆匀速下滑(B始终未与滑轮相碰),则( )
A.绳与杆的夹角为α时,B的速率为vsin α
B.绳与杆的夹角为α时,B的速率为vcos α
C.物体B也做匀速直线运动
D.物体B做匀加速直线运动
B
(不变)
例4、A、B两物体通过一根跨过光滑轻质定滑轮的轻绳相连放在水平面上,现物体A以v1的速度向右匀速运动,当绳被拉成与水平面夹角分别是α、β时,如图7所示,物体B的运动速度vB为(绳始终有拉力)( )
D
杆关联模型:
例5、如图所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动.当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面滑动的速度大小为v2,则v1、v2的关系是( )
A.v1=v2 B.v1=v2cos θ C.v1=v2tan θ D.v1=v2sin θ
C
【课后小结】
2、通过红蜡块的运动了解了合运动与分运动的概念以及
它们之间的关系。
1、如何建立平面直角坐标系去研究平面运动,以及如何
用轨迹方程去描述平面运动。
3、如何通过运动的合成从运动学的角度去研究合运动。
4、如何通过运动的分解去研究“关联速度”的问题。
专题:小船过河的问题
例:
练习1、如图所示,小船沿直线AB过河,船头始终垂直于河岸。若水流速度减小,为保持航线不变,下列措施与结论正确的是( )
A.减小船速,过河时间变长 B.减小船速,过河时间不变
C.增大船速,过河时间不变 D.增大船速,过河时间缩短
A
A
B
(不变)
思考:如果船速、水速恒定,
什么情况下渡河时间最短?
什么情况下渡河位移最短?
时间最短:
位移最短:
(一定)
A
B
C
练习2、
A
B
√
√
=2.5m/s
练习3.河水的流速随离河岸一侧的距离的变化关系如图甲所示,船在静水中的速度与时间的关系如图乙所示,若要使船以最短时间渡河,则( )
A.船渡河的最短时间是60 s
B.船在行驶过程中,船头始终与河岸垂直
C.船在河水中航行的轨迹是一条直线
D.船在河水中的最大速度是5 m/s
河宽
船速
√
√
【课后小结】
1、渡河时间最短:
垂直于河岸时
2、渡河位移最短:
垂直于河岸时
