3.5《长方体和正方体的体积》例1(课件)-五年级下册数学人教版(共18张PPT)
文档属性
| 名称 | 3.5《长方体和正方体的体积》例1(课件)-五年级下册数学人教版(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 858.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 12:43:55 | ||
图片预览




文档简介
(共18张PPT)
五年级·数学·人教版·下册
导学案课堂同步用书
第三单元 长方体和正方体
第5课 长方体和正方体的体积
1.掌握长方体、正方体的体积计算方法,会运用长方体、正方体的体积解决实际问题。
2.理解长方体、正方体统一的体积计算公式的推导过程。
3.积累活动经验,进一步培养应用意识。
答案
温习旧知
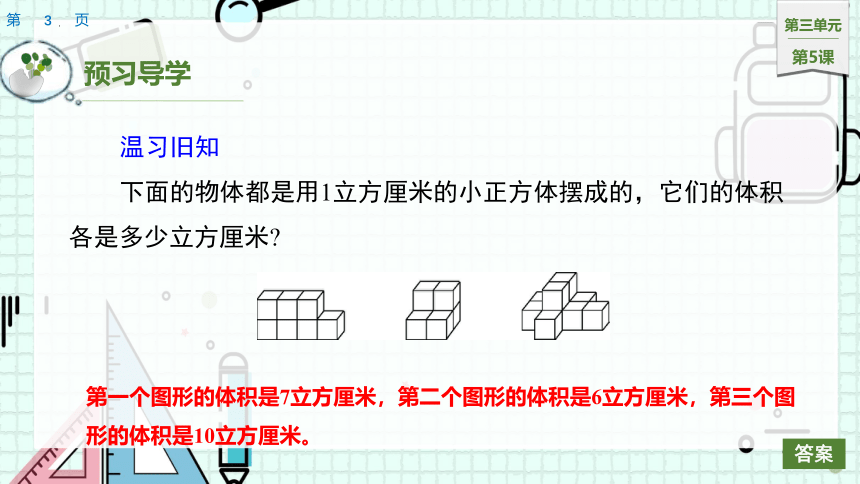
下面的物体都是用1立方厘米的小正方体摆成的,它们的体积各是多少立方厘米
第一个图形的体积是7立方厘米,第二个图形的体积是6立方厘米,第三个图形的体积是10立方厘米。
预习新知
摆一摆,算一算。
1.一个长方体的长、宽、高分别是5厘米、2厘米、2厘米,用1立方厘米的小正方体摆的话,需要多少个这样的小正方体
5×2×2=20(个)
答:需要20个这样的小正方体。
答案
2.一块棱长为2 cm的正方体,如果用1立方厘米的小正方体摆出来,一共要多少个这样的小正方体
2×2×2=8(个)
答:一共要8个这样的小正方体。
答案
(一)探究长方体的体积
1.小组合作学习。
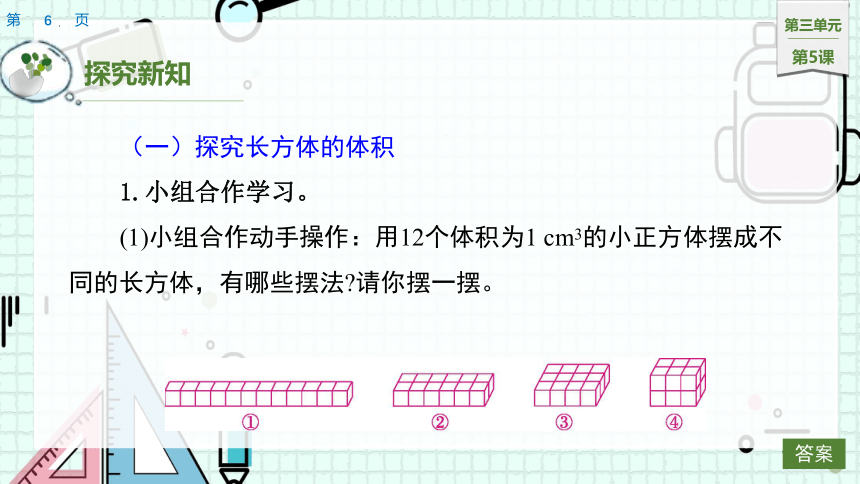
(1)小组合作动手操作:用12个体积为1 cm3的小正方体摆成不同的长方体,有哪些摆法 请你摆一摆。
答案
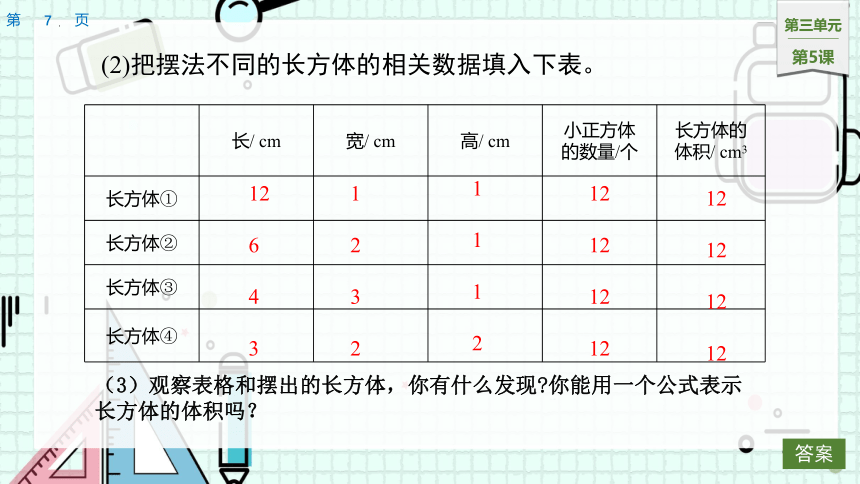
(2)把摆法不同的长方体的相关数据填入下表。
12
6
4
3
答案
长/ cm 宽/ cm 高/ cm 小正方体 的数量/个 长方体的
体积/ cm3
长方体①
长方体②
长方体③
长方体④
1
2
3
2
1
1
1
2
12
12
12
12
12
12
12
12
(3)观察表格和摆出的长方体,你有什么发现 你能用一个公式表示长方体的体积吗?
2.探究展示。
(1)小正方体的个数和长方体的体积的值相等。
(2)每行个数=长,行数=宽,层数=高,长方体体积=每行个数×行数×层数,所以长方体的体积=长×宽×高。
如果用字母V表示长方体的体积,用a、b、h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成V长=abh。
答案
(二)探究正方体的体积
1.自主学习。
根据长方体和正方体的关系,你能想出正方体的体积怎样计算吗
答案
答案
(1)正方体是特殊的长方体,即正方体是长、宽、高都相等的长方体。
(2)根据这个关系,可以推导出正方体体积的计算公式:正方体的体积=棱长×棱长×棱长。
(3)如果用V表示正方体的体积,用a表示正方体的棱长,那么正方体的体积计算公式可以写成V=a·a·a,一般写成V=a3。
2.检查释疑。
(三)教学例1
1.自主学习。
计算长方体或正方体的体积时,需要知道哪些条件呢 如何计算他们的体积?
V长=abh=7×3×4=84(cm3)
V正=a3=63=6×6×6=216(dm3)
答案
(四)探究长方体和正方体通用的体积计算公式。
我们已经知道正方体是特殊的长方体,那么是否可以用同一个计算公式表示它们的体积呢
1.自主学习。
什么叫做底面积?上图长方体、正方体的底面积该怎么计算呢
(1)长方体和正方体中,总有一个面与地面接触,通常把这个面叫作它的底面。这个底面的面积叫作底面积。
(2)长方体的底面积=长×宽 正方体的底面积=棱长×棱长
答案
小组讨论:
根据长方体、正方体的体积计算公式,可对体积计算公式进行推导。
如果用V表示长方体或正方体的体积,用S表示底面积,用h表示高,那么长方体、正方体统一的体积计算公式可以写成V=Sh。
答案
=( )×( )
底面积
底面积
看作高
底面积
高
即时巩固
1.一个正方体魔方的棱长为7 cm,这个魔方的体积是多少立方厘米
2.修路队要给一段长 150米、宽20米的水泥路面铺一层3厘米厚的沥青,一共需要沥青多少立方米
73=343(cm3)
答:这个魔方的体积是343立方厘米。
3厘米=0.03米 150×20×0.03=90(立方米)
答:一共需要沥青90立方米。
答案
答案
五、归纳总结
今天你有什么收获?
1.长方体的体积=长×宽×高,公式:V=abh。
2.正方体的体积=棱长×棱长×棱长,公式:V=a 。
3.长方体(正方体)的体积=底面积×高,公式:V=Sh。
答案
六、课堂检测1.填写下表中,长方体或正方体的相关数据。
底面积cm 1.5 1.5 43.2
高cm 5 7 2.6
体积cm 9 125 91 648
25
6
10.5
35
15
答案
2.一个长方体铁块长10dm,宽5dm,高4dm。每立方分米铁块重7.2kg,这个铁块重多少千克?
10×5×4=200dm
7.2×200=1440kg
答:这个铁块重1440千克。
END
感谢观看 下节课再会
五年级·数学·人教版·下册
导学案课堂同步用书
第三单元 长方体和正方体
第5课 长方体和正方体的体积
1.掌握长方体、正方体的体积计算方法,会运用长方体、正方体的体积解决实际问题。
2.理解长方体、正方体统一的体积计算公式的推导过程。
3.积累活动经验,进一步培养应用意识。
答案
温习旧知
下面的物体都是用1立方厘米的小正方体摆成的,它们的体积各是多少立方厘米
第一个图形的体积是7立方厘米,第二个图形的体积是6立方厘米,第三个图形的体积是10立方厘米。
预习新知
摆一摆,算一算。
1.一个长方体的长、宽、高分别是5厘米、2厘米、2厘米,用1立方厘米的小正方体摆的话,需要多少个这样的小正方体
5×2×2=20(个)
答:需要20个这样的小正方体。
答案
2.一块棱长为2 cm的正方体,如果用1立方厘米的小正方体摆出来,一共要多少个这样的小正方体
2×2×2=8(个)
答:一共要8个这样的小正方体。
答案
(一)探究长方体的体积
1.小组合作学习。
(1)小组合作动手操作:用12个体积为1 cm3的小正方体摆成不同的长方体,有哪些摆法 请你摆一摆。
答案
(2)把摆法不同的长方体的相关数据填入下表。
12
6
4
3
答案
长/ cm 宽/ cm 高/ cm 小正方体 的数量/个 长方体的
体积/ cm3
长方体①
长方体②
长方体③
长方体④
1
2
3
2
1
1
1
2
12
12
12
12
12
12
12
12
(3)观察表格和摆出的长方体,你有什么发现 你能用一个公式表示长方体的体积吗?
2.探究展示。
(1)小正方体的个数和长方体的体积的值相等。
(2)每行个数=长,行数=宽,层数=高,长方体体积=每行个数×行数×层数,所以长方体的体积=长×宽×高。
如果用字母V表示长方体的体积,用a、b、h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成V长=abh。
答案
(二)探究正方体的体积
1.自主学习。
根据长方体和正方体的关系,你能想出正方体的体积怎样计算吗
答案
答案
(1)正方体是特殊的长方体,即正方体是长、宽、高都相等的长方体。
(2)根据这个关系,可以推导出正方体体积的计算公式:正方体的体积=棱长×棱长×棱长。
(3)如果用V表示正方体的体积,用a表示正方体的棱长,那么正方体的体积计算公式可以写成V=a·a·a,一般写成V=a3。
2.检查释疑。
(三)教学例1
1.自主学习。
计算长方体或正方体的体积时,需要知道哪些条件呢 如何计算他们的体积?
V长=abh=7×3×4=84(cm3)
V正=a3=63=6×6×6=216(dm3)
答案
(四)探究长方体和正方体通用的体积计算公式。
我们已经知道正方体是特殊的长方体,那么是否可以用同一个计算公式表示它们的体积呢
1.自主学习。
什么叫做底面积?上图长方体、正方体的底面积该怎么计算呢
(1)长方体和正方体中,总有一个面与地面接触,通常把这个面叫作它的底面。这个底面的面积叫作底面积。
(2)长方体的底面积=长×宽 正方体的底面积=棱长×棱长
答案
小组讨论:
根据长方体、正方体的体积计算公式,可对体积计算公式进行推导。
如果用V表示长方体或正方体的体积,用S表示底面积,用h表示高,那么长方体、正方体统一的体积计算公式可以写成V=Sh。
答案
=( )×( )
底面积
底面积
看作高
底面积
高
即时巩固
1.一个正方体魔方的棱长为7 cm,这个魔方的体积是多少立方厘米
2.修路队要给一段长 150米、宽20米的水泥路面铺一层3厘米厚的沥青,一共需要沥青多少立方米
73=343(cm3)
答:这个魔方的体积是343立方厘米。
3厘米=0.03米 150×20×0.03=90(立方米)
答:一共需要沥青90立方米。
答案
答案
五、归纳总结
今天你有什么收获?
1.长方体的体积=长×宽×高,公式:V=abh。
2.正方体的体积=棱长×棱长×棱长,公式:V=a 。
3.长方体(正方体)的体积=底面积×高,公式:V=Sh。
答案
六、课堂检测1.填写下表中,长方体或正方体的相关数据。
底面积cm 1.5 1.5 43.2
高cm 5 7 2.6
体积cm 9 125 91 648
25
6
10.5
35
15
答案
2.一个长方体铁块长10dm,宽5dm,高4dm。每立方分米铁块重7.2kg,这个铁块重多少千克?
10×5×4=200dm
7.2×200=1440kg
答:这个铁块重1440千克。
END
感谢观看 下节课再会
