上海市民办文绮2023届高三下学期开学学情调研数学试题(含答案)
文档属性
| 名称 | 上海市民办文绮2023届高三下学期开学学情调研数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 581.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 15:40:37 | ||
图片预览



文档简介
上海市民办文绮2023届高三下学期开学学情调研
数学学科学情调研卷
一、填空题(本大题共有12小题,满分54分)考生应在答题纸相应编号的空格内直接填写结果,1-6题每个空格填对得4分,7-12题每个空格填对得5分.
1.已知集合与相等,则实数x的值为______.
2.复数z满足(其中i为虚数单位).则等于______.
3.若等式恒成立,则的值为______.
4.已知向量与的夹角为30°,,,则______.
5.已知,,则______.
6.已知,则的值为______.
7.在2022年8月15日那天,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量件y之间的一组数据如下表所示:
价格x 9 9.5 m 10.5 11
销售量y 11 n 8 6 5
可知,销售量y与价格x之间有较强的线性相关关系,其线性回归方程是,且,则其中的______.
8.已知等差数列的首项为2,公差为8,在中每相邻两项之间插入三个数,使它们与原数列的项一起构成一个新的等差数列,则数列______.
9.A、B、C、D四人去参加数学、物理、化学三科竞赛,每个同学只能参加一科竞赛,若A和B不参加同一科,且这三科都有人参加,则不同的选择种数是______.(用数字作答).
10.甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为,乙在每局中获胜的概率为,且各局胜负相互独立,设比赛停止时已达局数为,则______.
11.现有一款闯关游戏,共有4关,规则如下:在第n关要抛掷骰子n次,每次观察向上面的点数并做记录,如果这n次抛掷所出现的点数之和大于,则算闯过第n关,,2,3,4.假定每次闯关互不影响,则下列结论错误的序号是______.
(1)直接挑战第2关并过关的概率为;
(2)连续挑战前两关并过关的概率为;
(3)若直接挑战第3关,设“三个点数之和等于15”,“至少出现一个5点”,则;
(4)若直接挑战第4关,则过关的概率是.
12.已知函数,,若存在实数使在上有两个零点,则实数m的取值范围是______.
二、选择题(满分18分)本大题共有4小题每题有且只有一个正确答案,考生应在答题纸的相应位置,将代表正确正确选项的小方格涂黑.13-14选对每题得4分,15-16选对每题得5分,否则一律得零分.
13.在不超过18的素数中,随机选取两个不同的数,其和等于16的概率是( )
A. B. C. D.
14.如图,在正方体中,P是侧面上的一个动点,若点P到直线BC与直线的距离相等,则动点P的轨迹是下列哪种曲线的一部分( )
A.直线 B.圆 C.双曲线 D.抛物线
15.在某个独立重复实验中,事件A,B相互独立,且在一次实验中,事件A发生的概率为p,事件B发生的概率为,其中.若进行n次实验,记事件A发生的次数为X,事件B发生的次数为Y,事件AB发生的次数为Z,则下列说法正确的是( )
A. B.
C. D.
16.已知平面向量、、满足,对任意实数恒成立,则的最小值为( )
A. B. C. D.
三、解答题(满分76分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必须的步骤.
17.(木大题满分14分,第1小题6分,第2小题8分)
如图,在三棱锥中,底面ABC,D是PC的中点.已知,,,.
求:(1)三棱锥的体积;
(2)异面直线BC与AD所成的角的大小(结果用反三角函数值表示).
18.(本大题满分14分,第1小题7分,第2小题7分)
已知函数的最小值为-2.
(1)求实数m的值;
(2)在中,角A,B,C所对的边分别为a,b,c,若,,,求AC的长.
19.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
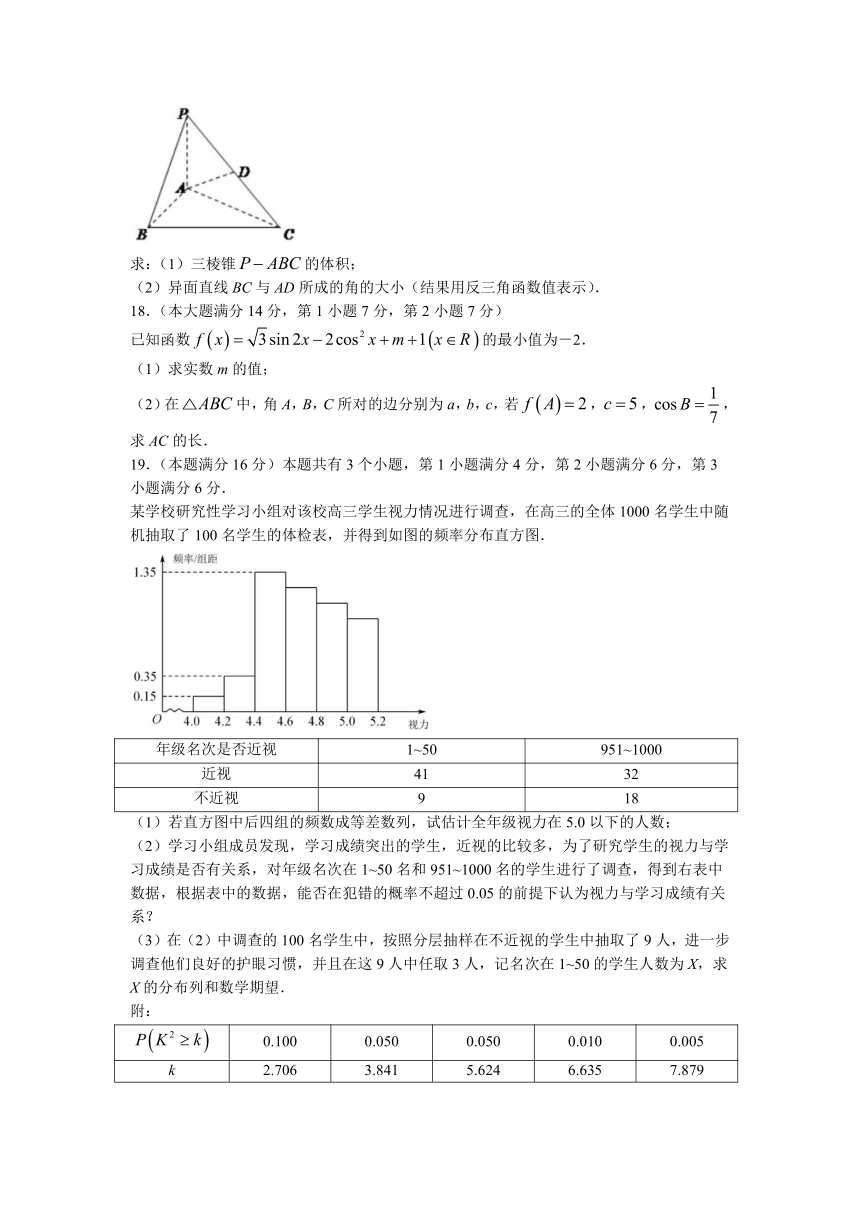
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
年级名次是否近视 1~50 951~1000
近视 41 32
不近视 9 18
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为X,求X的分布列和数学期望.
附:
0.100 0.050 0.050 0.010 0.005
k 2.706 3.841 5.624 6.635 7.879
20.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知二次曲线的方程:.
(1)分别求出方程表示椭圆和双曲线的条件;
(2)若双曲线与直线有公共点且实轴最长,求双曲线方程;
(3)m、n为正整数,且,是否存在两条曲线,,其交点P与点,满足?若存在,求m、n的值;若不存在,说明理由.
21.(本题满分18分)本题共有3小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
若函数在定义域内给定区间上存在,满足,则称函数是区间上的“平均值函数”,是它的平均值点.
(1)已知函数是区间的“平均值函数”,求该函数的平均值点;
(2)当函数是区间上的“平均值函数”,且有两个不同的平均值点时,求实数m的取值范围;
(3)是否存在区间,使得函数是区间上的“平均值函数”?若存在,求出所有满足条件的区间;若不存在,请说明理由.
参考答案
一、填空题
1.2 2.1 3.-1 4. 5.0.06 6. 7.10 8.4046
9.30 10. 11.(1)(2)(3)(4) 12.
二、选择题
13.B 14.D 15.C 16.B
三、解答题
17.【详解】:(1)因为,,,所以,
又底面ABC,
所以三棱锥的体积为;
(2)取PB的中点E,连接AE,DE,则,
所以∠ADE(或其补角)是异面直线BC与AD所成的角.
在中,,,,
由余弦定理可得,所以.
所以异面直线BC与AD所成的角.
18.【详解】:(1),
∵的最小值为-2,∴,解得.
(2)由得,
∵,∴,
∴,解得,
∵,,∴,
∴.
由正弦定理,得,得,所以.
19.【详解】:(1)设各组的频率为.
由图可知.第一组有3人,第二组7人,第三组27人,
因为后四组的频数成等差数列,所以后四组频数依次为27,24,21,18,
所以视力在5.0以下的频率为人,
故全年级视力在5.0以下的人数约为;
(2)
∵观测值为,
∴在犯错误的概率不超过0.05的前提下有95%的把握认为学生的视力与学生的学习成绩有关系.
(3)据题意知,9人中年级名次在1~50名和951~1000名的人数分别为3人和6人,所以X的所有可能取值为0,1,2,3
,,
,
X 0 1 2 3
P
所以.
20.【详解】:(1)当且仅当时,方程表示椭圆;
当时,方程表示双曲线;
(2)化简,
因为双曲线与直线有公共点,所以或或,
双曲线的实轴长为,当时,双曲线实轴长最长为.
此时双曲线方程为;
(3)由(1)知,,是椭圆,,,,是双曲线,
任意两椭圆之间无公共点,任意两双曲线之间也无公共点
设,,,,
根据椭圆、双曲线定义及(即),
所以,所以.
所以这样的,存在,且或或.
21.【详解】:(1)设为平均值点,则,解得,
又,故该函数的平均值点为;
(2)设是平均值点,则由,得.
故关于x的方程在区间内有两个不同的解
记,则
令,得驻点.
x 1
极小值
因此,函数在上严格减,在上严格增,
又,,
故实数m的取值范围是.
(3)令,
假设存在区间,使得函数是区间上的“平均值函数”,则存在
在区间上有解,
又,当时,,当时.,
所以在上单调递增,在上单调递减.
所以,
即,即,即,即,
又因为,即,所以与相矛盾.
数学学科学情调研卷
一、填空题(本大题共有12小题,满分54分)考生应在答题纸相应编号的空格内直接填写结果,1-6题每个空格填对得4分,7-12题每个空格填对得5分.
1.已知集合与相等,则实数x的值为______.
2.复数z满足(其中i为虚数单位).则等于______.
3.若等式恒成立,则的值为______.
4.已知向量与的夹角为30°,,,则______.
5.已知,,则______.
6.已知,则的值为______.
7.在2022年8月15日那天,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量件y之间的一组数据如下表所示:
价格x 9 9.5 m 10.5 11
销售量y 11 n 8 6 5
可知,销售量y与价格x之间有较强的线性相关关系,其线性回归方程是,且,则其中的______.
8.已知等差数列的首项为2,公差为8,在中每相邻两项之间插入三个数,使它们与原数列的项一起构成一个新的等差数列,则数列______.
9.A、B、C、D四人去参加数学、物理、化学三科竞赛,每个同学只能参加一科竞赛,若A和B不参加同一科,且这三科都有人参加,则不同的选择种数是______.(用数字作答).
10.甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为,乙在每局中获胜的概率为,且各局胜负相互独立,设比赛停止时已达局数为,则______.
11.现有一款闯关游戏,共有4关,规则如下:在第n关要抛掷骰子n次,每次观察向上面的点数并做记录,如果这n次抛掷所出现的点数之和大于,则算闯过第n关,,2,3,4.假定每次闯关互不影响,则下列结论错误的序号是______.
(1)直接挑战第2关并过关的概率为;
(2)连续挑战前两关并过关的概率为;
(3)若直接挑战第3关,设“三个点数之和等于15”,“至少出现一个5点”,则;
(4)若直接挑战第4关,则过关的概率是.
12.已知函数,,若存在实数使在上有两个零点,则实数m的取值范围是______.
二、选择题(满分18分)本大题共有4小题每题有且只有一个正确答案,考生应在答题纸的相应位置,将代表正确正确选项的小方格涂黑.13-14选对每题得4分,15-16选对每题得5分,否则一律得零分.
13.在不超过18的素数中,随机选取两个不同的数,其和等于16的概率是( )
A. B. C. D.
14.如图,在正方体中,P是侧面上的一个动点,若点P到直线BC与直线的距离相等,则动点P的轨迹是下列哪种曲线的一部分( )
A.直线 B.圆 C.双曲线 D.抛物线
15.在某个独立重复实验中,事件A,B相互独立,且在一次实验中,事件A发生的概率为p,事件B发生的概率为,其中.若进行n次实验,记事件A发生的次数为X,事件B发生的次数为Y,事件AB发生的次数为Z,则下列说法正确的是( )
A. B.
C. D.
16.已知平面向量、、满足,对任意实数恒成立,则的最小值为( )
A. B. C. D.
三、解答题(满分76分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必须的步骤.
17.(木大题满分14分,第1小题6分,第2小题8分)
如图,在三棱锥中,底面ABC,D是PC的中点.已知,,,.
求:(1)三棱锥的体积;
(2)异面直线BC与AD所成的角的大小(结果用反三角函数值表示).
18.(本大题满分14分,第1小题7分,第2小题7分)
已知函数的最小值为-2.
(1)求实数m的值;
(2)在中,角A,B,C所对的边分别为a,b,c,若,,,求AC的长.
19.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
年级名次是否近视 1~50 951~1000
近视 41 32
不近视 9 18
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为X,求X的分布列和数学期望.
附:
0.100 0.050 0.050 0.010 0.005
k 2.706 3.841 5.624 6.635 7.879
20.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知二次曲线的方程:.
(1)分别求出方程表示椭圆和双曲线的条件;
(2)若双曲线与直线有公共点且实轴最长,求双曲线方程;
(3)m、n为正整数,且,是否存在两条曲线,,其交点P与点,满足?若存在,求m、n的值;若不存在,说明理由.
21.(本题满分18分)本题共有3小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
若函数在定义域内给定区间上存在,满足,则称函数是区间上的“平均值函数”,是它的平均值点.
(1)已知函数是区间的“平均值函数”,求该函数的平均值点;
(2)当函数是区间上的“平均值函数”,且有两个不同的平均值点时,求实数m的取值范围;
(3)是否存在区间,使得函数是区间上的“平均值函数”?若存在,求出所有满足条件的区间;若不存在,请说明理由.
参考答案
一、填空题
1.2 2.1 3.-1 4. 5.0.06 6. 7.10 8.4046
9.30 10. 11.(1)(2)(3)(4) 12.
二、选择题
13.B 14.D 15.C 16.B
三、解答题
17.【详解】:(1)因为,,,所以,
又底面ABC,
所以三棱锥的体积为;
(2)取PB的中点E,连接AE,DE,则,
所以∠ADE(或其补角)是异面直线BC与AD所成的角.
在中,,,,
由余弦定理可得,所以.
所以异面直线BC与AD所成的角.
18.【详解】:(1),
∵的最小值为-2,∴,解得.
(2)由得,
∵,∴,
∴,解得,
∵,,∴,
∴.
由正弦定理,得,得,所以.
19.【详解】:(1)设各组的频率为.
由图可知.第一组有3人,第二组7人,第三组27人,
因为后四组的频数成等差数列,所以后四组频数依次为27,24,21,18,
所以视力在5.0以下的频率为人,
故全年级视力在5.0以下的人数约为;
(2)
∵观测值为,
∴在犯错误的概率不超过0.05的前提下有95%的把握认为学生的视力与学生的学习成绩有关系.
(3)据题意知,9人中年级名次在1~50名和951~1000名的人数分别为3人和6人,所以X的所有可能取值为0,1,2,3
,,
,
X 0 1 2 3
P
所以.
20.【详解】:(1)当且仅当时,方程表示椭圆;
当时,方程表示双曲线;
(2)化简,
因为双曲线与直线有公共点,所以或或,
双曲线的实轴长为,当时,双曲线实轴长最长为.
此时双曲线方程为;
(3)由(1)知,,是椭圆,,,,是双曲线,
任意两椭圆之间无公共点,任意两双曲线之间也无公共点
设,,,,
根据椭圆、双曲线定义及(即),
所以,所以.
所以这样的,存在,且或或.
21.【详解】:(1)设为平均值点,则,解得,
又,故该函数的平均值点为;
(2)设是平均值点,则由,得.
故关于x的方程在区间内有两个不同的解
记,则
令,得驻点.
x 1
极小值
因此,函数在上严格减,在上严格增,
又,,
故实数m的取值范围是.
(3)令,
假设存在区间,使得函数是区间上的“平均值函数”,则存在
在区间上有解,
又,当时,,当时.,
所以在上单调递增,在上单调递减.
所以,
即,即,即,即,
又因为,即,所以与相矛盾.
同课章节目录
