鲁教版九年级数学上册 第二章 直角三角形的边角关系 综合素质评价试题(含答案)
文档属性
| 名称 | 鲁教版九年级数学上册 第二章 直角三角形的边角关系 综合素质评价试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 510.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 21:22:15 | ||
图片预览




文档简介
第二章 直角三角形的边角关系 综合素质评价
一、选择题(每题3分,共30分)
1.【2022·烟台期末】在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,则下列正确的是( )
A.sinA= B.cosA= C.tanA= D.cosB=
2.【2023·泰安市东平县月考】在△ABC中,∠C=90°,若sinA=,则cosB的值为( )
A. B. C.2 D.
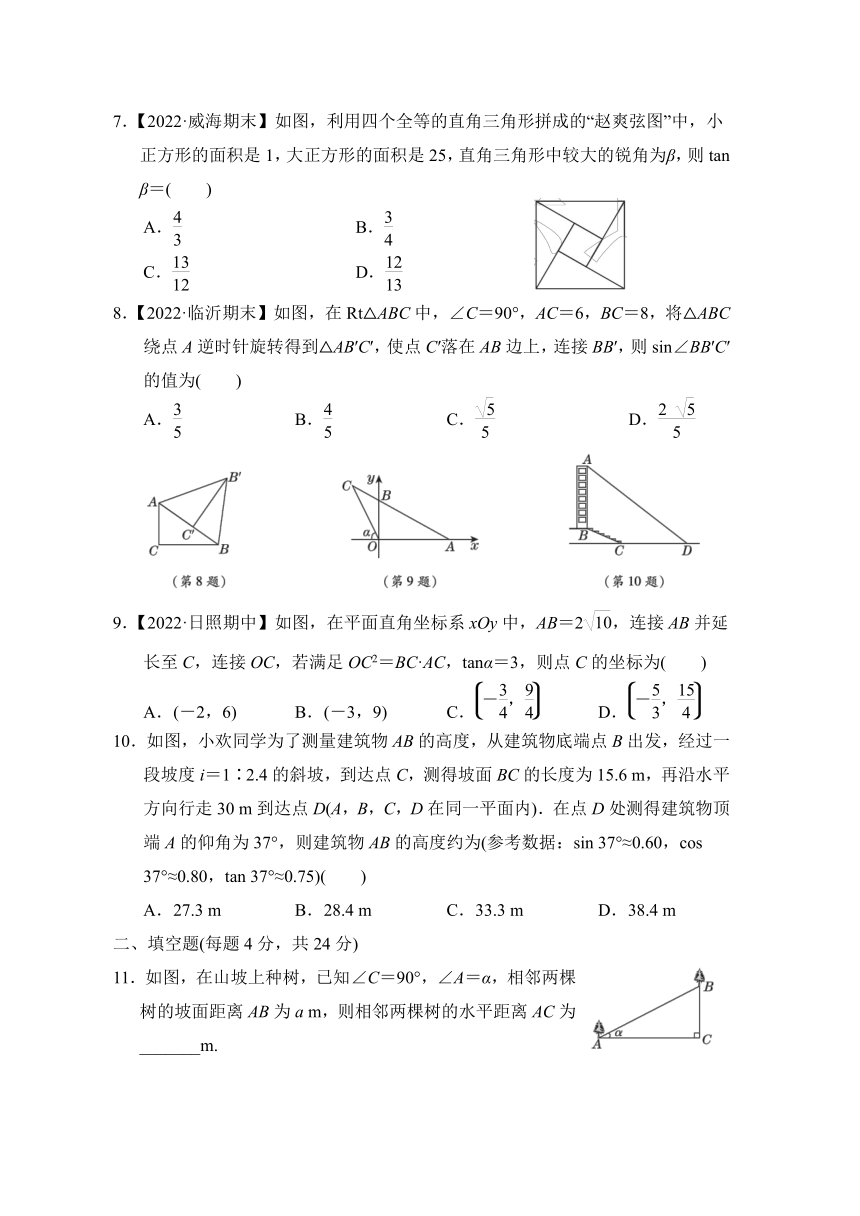
3.【2022·聊城期末】如图,在△ABC中,点A、B、C都在正方形网格的格点上,则tan∠BAC=( )
A.1 B. C. D.
4.【教材P51习题T2变式】如图,某水库大坝的横断面是梯形ABCD,坝高DE=
5 m,斜坡BC的坡比为5∶12,则斜坡BC=( )
A.13 m B.8 m C.18 m D.12 m
5.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔6海里的A处,若海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.6cos 55°海里 C.6sin 55°海里 D.6tan 55°海里
6.【2022·淄博期末】如图,∠ACB=45°,∠PRQ=125°,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2
B.h1C.h1>h2
D.以上都有可能
7.【2022·威海期末】如图,利用四个全等的直角三角形拼成的“赵爽弦图”中,小正方形的面积是1,大正方形的面积是25,直角三角形中较大的锐角为β,则tan β=( )
A. B.
C. D.
8.【2022·临沂期末】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,连接BB′,则sin∠BB′C′的值为( )
A. B. C. D.
9.【2022·日照期中】如图,在平面直角坐标系xOy中,AB=2,连接AB并延长至C,连接OC,若满足OC2=BC·AC,tanα=3,则点C的坐标为( )
A.(-2,6) B.(-3,9) C. D.
10.如图,小欢同学为了测量建筑物AB的高度,从建筑物底端点B出发,经过一段坡度i=1∶2.4的斜坡,到达点C,测得坡面BC的长度为15.6 m,再沿水平方向行走30 m到达点D(A,B,C,D在同一平面内).在点D处测得建筑物顶端A的仰角为37°,则建筑物AB的高度约为(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)( )
A.27.3 m B.28.4 m C.33.3 m D.38.4 m
二、填空题(每题4分,共24分)
11.如图,在山坡上种树,已知∠C=90°,∠A=α,相邻两棵树的坡面距离AB为a m,则相邻两棵树的水平距离AC为_______m.
12.如图,点P(12,a)在反比例函数y=的图象上,PH⊥x轴于H,则tan∠POH的值为_______.
13.【2023·威海乳山校级月考】某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2米,则这个坡面的坡度为_______.
14.【2023·威海文登区联考】在△ABC中,sinB=,AC=2,AD是BC边上的高,∠ACD=45°,则BC的长为_______.
15.【母题:教材P56复习题T14】如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6 m,则旗杆AB的高度为_______m.
16.【2022·绵阳】如图,测量船以20海里每小时的速度沿正东方向航行并对某海岛进行测量,测量船在A处测得海岛上观测点D位于北偏东15°方向上,观测点C位于北偏东45°方向上,航行半小时到达B点,这时测得海岛上观测点C位于北偏西45°方向上,若CD与AB平行,则CD=_______海里(计算结果不取近似值).
三、解答题(17~19题每题10分,其余每题12分,共66分)
17.计算:
(1)【2022·乐山】sin 30°+-2-1; (2)+4cos 60°·sin 45°-.
18.【母题:教材P42例3】在Rt△ABC中,∠C=90°,AC=15,∠B=60°,求这个三角形的其他元素.
19.【2022·菏泽】荷泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37°减至30°,已知原电梯坡面AB的长为8米,更换后的电梯坡面为AD,点B延伸至点D,求BD的长.(结果精确到0.1米.参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
20.【2022·无锡】如图,已知四边形ABCD为矩形,AB=2,BC=4,点E在BC上,CE=AE,将△ABC沿AC翻折得到△AFC,连接EF.
(1)求EF的长;
(2)求sin∠CEF的值.
21.【2023·威海文登区联考】“五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AB,用绳子拉直AD后系在树干EF上的点E处,使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,AC=AD=2 m,
BF=3 m.
(1)天睛时打开“天幕”,若α=65°,求遮阳宽度CD(结果精确到0.1 m);
(2)下雨时收拢“天幕”,α从65°减小到45°,求点E下降的高度(结果精确到0.1 m).
(参考数据:sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14,≈1.41)
22.【2022·泰州】小强在物理课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验.如图,老师在该厂房顶部安装一平面镜MN,MN与墙面AB所成的角∠MNB=118°,厂房高AB= 8 m,房顶AM与水平地面平行,小强在点M的正下方C处从平面镜观察,能看到的水平地面上最远处D到他的距离CD是多少?(结果精确到0.1 m,参考数据:sin 34°≈0.56, tan 34°≈0.67,tan 56°≈ 1.48)
答案
一、1.B 【点拨】因为∠ACB=90°,CD⊥AB,所以sinA==,cosA==,tanA==,cosB==.故选B.
2.A 【点拨】∵∠C=90°,∴∠A+∠B=90°,∴sinA=cosB=.故选A.
3.A 【点拨】由题图可知AB==,AC==,BC==,∴AC2+BC2=AB2,∴△ABC为直角三角形,且∠BCA=90°,
∴tan∠BAC==1.故选A.
4.A 【点拨】过点C作CF⊥AB,垂足为F.
∵坝高DE=5 m,CF⊥AB,∴DE=CF=5 m.又∵斜坡BC的坡比为5∶12,∴BF=12 m,∴在Rt△BCF中,BC===13(m).
故选A.
5.B 【点拨】由题易知∠B=90°,∠A=55°,AP=6海里,∴AB=AP·cos A=6cos 55°海里.故选B.
6.B 【点拨】如图,分别作出两个三角形的高h1,h2.
∵∠ACB=45°,AC=5,∴h1=AC×sin 45°=5sin 45°.∵∠PRQ=125°,PR=5,∴h2=PR×sin(180°-125°)=5sin 55°.∵sin 55°>sin 45°,∴h2>h1.故选B.
7.A 【点拨】由题意知,小正方形的边长为1,大正方形的边长为5.设直角三角形中较小直角边的边长为x,则有(1+x)2+x2=25.解得x=3(负值不合题意,舍去),∴较长直角边的边长为x+1=4,∴tan β=.故选A.
8.C 【点拨】在Rt△ABC中,∠C=90°,AC=6,BC=8,由勾股定理得AB===10.∵△ABC绕点A逆时针旋转得到△AB′C′,∴AC′=AC=6,B′C′=BC=8,∠AC′B′=∠C=90°. ∴BC′=AB-AC′=10-6=4.
∴在Rt△BB′C′中,由勾股定理得BB′===4.
∴sin∠BB′C′===.故选C.
9.C 【点拨】∵OC2=BC·AC,∴=.又∵∠C=∠C,∴△OBC∽△AOC,∴∠A=∠COB.∵α+∠COB=90°,∠A+∠ABO=90°,∴∠ABO=α.
∵tanα=3,∴tan∠ABO==3,∴OA=3OB.由勾股定理可得OA2+OB2=AB2,即9OB2+OB2=(2)2,∴OB=2,∴OA=6.∴tanA==.如图,过点C作CD⊥x轴于点D.∵tanα=3,∴设C(-m,3m),m>0.∴AD=6+m.
∵tanA=,∴=,即=,解得m=.经检验,m=是原方程的解.∴点C的坐标为.故选C.
10.A 【点拨】设AB的延长线与DC的延长线交于点E.
∵BC=15.6 m,斜坡BC的坡度i=1∶2.4=,
∴cos∠BCE=,sin∠BCE=,∴EC=BC·cos∠BCE=15.6×=14.4(m),BE=BC·sin∠BCE=15.6×=6(m),∴ED=EC+CD=14.4+30=44.4(m).
又∵∠D=37°,∴AE=ED·tan 37°≈44.4×0.75=33.3(m),
∴AB=AE-BE≈33.3-6=27.3(m).
二、11.acosα 【点拨】∵∠C=90°,∠A=α,AB=a m,∴AC=AB·cosα=
acosα m.
12. 【点拨】∵点P(12,a)在反比例函数y=的图象上,∴a==5.
∵PH⊥x轴于H,∴PH=5,OH=12,∴tan∠POH=.
13.1∶2 【点拨】由勾股定理得斜坡的水平宽度为=4(米).则这个坡面的坡度i=2∶4=1∶2.
14.2+2或2-2 【点拨】分情况讨论:如图①,当AD在△ABC的内部时,∵AD⊥BC,即∠ADB=∠ADC=90°.在Rt△ACD中,∠ACD=45°,
∴∠DAC=45°.∵AC=2,∴DC=AD=AC·sin 45°=2 ×=2.
在Rt△ABD中,sinB=,AD=2,∴sinB==,解得AB=4.根据勾股定理得BD===2.∴BC=BD+DC=2+2.如图②,当AD在△ABC的外部时,∵AD是BC边上的高,∴∠D=90°.
在Rt△ACD中,∠ACD=45°,∴∠DAC=45°.∴AD=DC=AC·sin 45°=2.
在Rt△ABD中,sinB=,∴sinB==,∴AB=4.∴BD===2.∴BC=BD-DC=2-2.综上,BC的长为2+2或2-2.
15.14.4 【点拨】过点D作DE⊥AB于E,则∠AED=90°,四边形 BCDE是矩形,∴BE=CD=9.6 m,∠CDE=∠DEA=90°,∴∠ADC=90°+30°=120°.∵∠ACB=60°,∴∠ACD=30°,∴∠CAD=30°=∠ACD,∴AD=CD=
9.6 m.在Rt△ADE中,∠ADE=30°,∴AE=AD=4.8 m,∴AB=AE+BE=4.8+9.6=14.4(m).
16.(5-5) 【点拨】如图,过点D作DE⊥AC,垂足为E.依题意得,AB=20×
=10(海里),∠FAD=15°,∠FAC=45°,∠FAB=90°,∠ABC=45°,∴∠CAB=90°-45°=45°,∠DAC=
∠FAC-∠FAD=30°,∴∠ACB=180°-∠CAB-∠CBA=90°.在Rt△ACB中,AC=AB·sin 45°=10×=5(海里).设DE=x海里,在Rt△DAE中,AE===x(海里).∵DC∥AB,∴∠DCA=∠CAB=45°.在Rt△DEC中,CE==x海里,∴DC=x海里.∵AE+EC=AC,∴x+x=5,解得x=,∴DC=×=(5-5)海里.
三、17.解:(1)原式=+3-=3.
(2)原式=1+4××-=1+-(2-)=-1++.
18.解:∵∠C=90°,∠B=60°,
∴∠A=90°-∠B=90°-60°=30°.
∴BC=AC·tan A=15×=5.
∴AB=2BC=2×5=10.
19.解:在Rt△ABC中,AB=8米,∠ABC=37°,
∴AC=AB·sin∠ABC≈8×0.60=4.8(米),
BC=AB·cos∠ABC≈8×0.80=6.4(米).
在Rt△ADC中,∠ADC=30°,
∴CD=≈≈8.3(米),
∴BD=CD-BC≈8.3-6.4=1.9(米).
答:BD的长约为1.9米.
20.解:(1)如图,设BE=x,则EC=4-x,
∴AE=EC=4-x.
在Rt△ABE中,AB2+BE2=AE2,
∴(2)2+x2=(4-x)2,解得x=1.
∴BE=1,AE=CE=3.
∵AE=EC,∴∠1=∠2.
∵∠ABC=90°,∴∠CAB=90°-∠2,
∴∠CAB=90°-∠1.
由折叠可知△FAC≌△BAC,
∴∠FAC=∠CAB=90°-∠1,AF=AB=2 ,
∴∠FAC+∠1=90°,即∠FAE=90°.
在Rt△FAE中,EF===.
(2)如图,过F作FM⊥BC于M,
∴∠FME=∠FMC=90°.
设EM=a,则MC=3-a.
在Rt△FME中,FM2=FE2-EM2,
在Rt△FMC中,FM2=FC2-MC2,
∴FE2-EM2=FC2-MC2,
∴()2-a2=42-(3-a)2,∴a=.
∴EM=,∴FM== ,
∴sin∠CEF=== .
21.解:(1)∵AD=AC=2 m,∠AOD=90°,
∴CD=2OD.
在Rt△AOD中,∠OAD=α=65°,
∴OD=AD·sinα=2×sin 65°≈2×0.91=1.82(m),
∴CD=2OD≈3.6 m.
答:遮阳宽度CD约为3.6 m.
(2)如图,过点E作EH⊥AB于H,则∠BHE=90°.
∵AB⊥BF,EF⊥BF,∴∠ABF=∠EFB=90°,
∴四边形BFEH为矩形,∴EH=BF=3 m.
在Rt△AHE中,tanα=,∴AH=.
当α=65°时,AH=≈≈1.4(m),
当α=45°时,AH===3(m),
∴当α从65°减小到45°时,点E下降的高度约为3-1.4=1.6(m).
22.解:如图,过M点作ME⊥MN交CD于E点,则∠NME=90°.
由题易得四边形AMCB为矩形,
∴MC=AB=8 m,AB∥CM,
∴∠NMC=180°-∠BNM=180°-118°=62°.
∵地面上的点D经过平面镜MN反射后落在点C,
∴∠EMD=∠EMC=90°-∠NMC=90°-62°=28°,
∴∠CMD=56°.
在Rt△CMD中,tan∠CMD=,
即1.48≈,∴CD≈11.8 m.
即水平地面上最远处D到小强的距离CD约是11.8 m.
一、选择题(每题3分,共30分)
1.【2022·烟台期末】在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,则下列正确的是( )
A.sinA= B.cosA= C.tanA= D.cosB=
2.【2023·泰安市东平县月考】在△ABC中,∠C=90°,若sinA=,则cosB的值为( )
A. B. C.2 D.
3.【2022·聊城期末】如图,在△ABC中,点A、B、C都在正方形网格的格点上,则tan∠BAC=( )
A.1 B. C. D.
4.【教材P51习题T2变式】如图,某水库大坝的横断面是梯形ABCD,坝高DE=
5 m,斜坡BC的坡比为5∶12,则斜坡BC=( )
A.13 m B.8 m C.18 m D.12 m
5.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔6海里的A处,若海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.6cos 55°海里 C.6sin 55°海里 D.6tan 55°海里
6.【2022·淄博期末】如图,∠ACB=45°,∠PRQ=125°,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2
B.h1
D.以上都有可能
7.【2022·威海期末】如图,利用四个全等的直角三角形拼成的“赵爽弦图”中,小正方形的面积是1,大正方形的面积是25,直角三角形中较大的锐角为β,则tan β=( )
A. B.
C. D.
8.【2022·临沂期末】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,连接BB′,则sin∠BB′C′的值为( )
A. B. C. D.
9.【2022·日照期中】如图,在平面直角坐标系xOy中,AB=2,连接AB并延长至C,连接OC,若满足OC2=BC·AC,tanα=3,则点C的坐标为( )
A.(-2,6) B.(-3,9) C. D.
10.如图,小欢同学为了测量建筑物AB的高度,从建筑物底端点B出发,经过一段坡度i=1∶2.4的斜坡,到达点C,测得坡面BC的长度为15.6 m,再沿水平方向行走30 m到达点D(A,B,C,D在同一平面内).在点D处测得建筑物顶端A的仰角为37°,则建筑物AB的高度约为(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)( )
A.27.3 m B.28.4 m C.33.3 m D.38.4 m
二、填空题(每题4分,共24分)
11.如图,在山坡上种树,已知∠C=90°,∠A=α,相邻两棵树的坡面距离AB为a m,则相邻两棵树的水平距离AC为_______m.
12.如图,点P(12,a)在反比例函数y=的图象上,PH⊥x轴于H,则tan∠POH的值为_______.
13.【2023·威海乳山校级月考】某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2米,则这个坡面的坡度为_______.
14.【2023·威海文登区联考】在△ABC中,sinB=,AC=2,AD是BC边上的高,∠ACD=45°,则BC的长为_______.
15.【母题:教材P56复习题T14】如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6 m,则旗杆AB的高度为_______m.
16.【2022·绵阳】如图,测量船以20海里每小时的速度沿正东方向航行并对某海岛进行测量,测量船在A处测得海岛上观测点D位于北偏东15°方向上,观测点C位于北偏东45°方向上,航行半小时到达B点,这时测得海岛上观测点C位于北偏西45°方向上,若CD与AB平行,则CD=_______海里(计算结果不取近似值).
三、解答题(17~19题每题10分,其余每题12分,共66分)
17.计算:
(1)【2022·乐山】sin 30°+-2-1; (2)+4cos 60°·sin 45°-.
18.【母题:教材P42例3】在Rt△ABC中,∠C=90°,AC=15,∠B=60°,求这个三角形的其他元素.
19.【2022·菏泽】荷泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37°减至30°,已知原电梯坡面AB的长为8米,更换后的电梯坡面为AD,点B延伸至点D,求BD的长.(结果精确到0.1米.参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
20.【2022·无锡】如图,已知四边形ABCD为矩形,AB=2,BC=4,点E在BC上,CE=AE,将△ABC沿AC翻折得到△AFC,连接EF.
(1)求EF的长;
(2)求sin∠CEF的值.
21.【2023·威海文登区联考】“五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AB,用绳子拉直AD后系在树干EF上的点E处,使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,AC=AD=2 m,
BF=3 m.
(1)天睛时打开“天幕”,若α=65°,求遮阳宽度CD(结果精确到0.1 m);
(2)下雨时收拢“天幕”,α从65°减小到45°,求点E下降的高度(结果精确到0.1 m).
(参考数据:sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14,≈1.41)
22.【2022·泰州】小强在物理课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验.如图,老师在该厂房顶部安装一平面镜MN,MN与墙面AB所成的角∠MNB=118°,厂房高AB= 8 m,房顶AM与水平地面平行,小强在点M的正下方C处从平面镜观察,能看到的水平地面上最远处D到他的距离CD是多少?(结果精确到0.1 m,参考数据:sin 34°≈0.56, tan 34°≈0.67,tan 56°≈ 1.48)
答案
一、1.B 【点拨】因为∠ACB=90°,CD⊥AB,所以sinA==,cosA==,tanA==,cosB==.故选B.
2.A 【点拨】∵∠C=90°,∴∠A+∠B=90°,∴sinA=cosB=.故选A.
3.A 【点拨】由题图可知AB==,AC==,BC==,∴AC2+BC2=AB2,∴△ABC为直角三角形,且∠BCA=90°,
∴tan∠BAC==1.故选A.
4.A 【点拨】过点C作CF⊥AB,垂足为F.
∵坝高DE=5 m,CF⊥AB,∴DE=CF=5 m.又∵斜坡BC的坡比为5∶12,∴BF=12 m,∴在Rt△BCF中,BC===13(m).
故选A.
5.B 【点拨】由题易知∠B=90°,∠A=55°,AP=6海里,∴AB=AP·cos A=6cos 55°海里.故选B.
6.B 【点拨】如图,分别作出两个三角形的高h1,h2.
∵∠ACB=45°,AC=5,∴h1=AC×sin 45°=5sin 45°.∵∠PRQ=125°,PR=5,∴h2=PR×sin(180°-125°)=5sin 55°.∵sin 55°>sin 45°,∴h2>h1.故选B.
7.A 【点拨】由题意知,小正方形的边长为1,大正方形的边长为5.设直角三角形中较小直角边的边长为x,则有(1+x)2+x2=25.解得x=3(负值不合题意,舍去),∴较长直角边的边长为x+1=4,∴tan β=.故选A.
8.C 【点拨】在Rt△ABC中,∠C=90°,AC=6,BC=8,由勾股定理得AB===10.∵△ABC绕点A逆时针旋转得到△AB′C′,∴AC′=AC=6,B′C′=BC=8,∠AC′B′=∠C=90°. ∴BC′=AB-AC′=10-6=4.
∴在Rt△BB′C′中,由勾股定理得BB′===4.
∴sin∠BB′C′===.故选C.
9.C 【点拨】∵OC2=BC·AC,∴=.又∵∠C=∠C,∴△OBC∽△AOC,∴∠A=∠COB.∵α+∠COB=90°,∠A+∠ABO=90°,∴∠ABO=α.
∵tanα=3,∴tan∠ABO==3,∴OA=3OB.由勾股定理可得OA2+OB2=AB2,即9OB2+OB2=(2)2,∴OB=2,∴OA=6.∴tanA==.如图,过点C作CD⊥x轴于点D.∵tanα=3,∴设C(-m,3m),m>0.∴AD=6+m.
∵tanA=,∴=,即=,解得m=.经检验,m=是原方程的解.∴点C的坐标为.故选C.
10.A 【点拨】设AB的延长线与DC的延长线交于点E.
∵BC=15.6 m,斜坡BC的坡度i=1∶2.4=,
∴cos∠BCE=,sin∠BCE=,∴EC=BC·cos∠BCE=15.6×=14.4(m),BE=BC·sin∠BCE=15.6×=6(m),∴ED=EC+CD=14.4+30=44.4(m).
又∵∠D=37°,∴AE=ED·tan 37°≈44.4×0.75=33.3(m),
∴AB=AE-BE≈33.3-6=27.3(m).
二、11.acosα 【点拨】∵∠C=90°,∠A=α,AB=a m,∴AC=AB·cosα=
acosα m.
12. 【点拨】∵点P(12,a)在反比例函数y=的图象上,∴a==5.
∵PH⊥x轴于H,∴PH=5,OH=12,∴tan∠POH=.
13.1∶2 【点拨】由勾股定理得斜坡的水平宽度为=4(米).则这个坡面的坡度i=2∶4=1∶2.
14.2+2或2-2 【点拨】分情况讨论:如图①,当AD在△ABC的内部时,∵AD⊥BC,即∠ADB=∠ADC=90°.在Rt△ACD中,∠ACD=45°,
∴∠DAC=45°.∵AC=2,∴DC=AD=AC·sin 45°=2 ×=2.
在Rt△ABD中,sinB=,AD=2,∴sinB==,解得AB=4.根据勾股定理得BD===2.∴BC=BD+DC=2+2.如图②,当AD在△ABC的外部时,∵AD是BC边上的高,∴∠D=90°.
在Rt△ACD中,∠ACD=45°,∴∠DAC=45°.∴AD=DC=AC·sin 45°=2.
在Rt△ABD中,sinB=,∴sinB==,∴AB=4.∴BD===2.∴BC=BD-DC=2-2.综上,BC的长为2+2或2-2.
15.14.4 【点拨】过点D作DE⊥AB于E,则∠AED=90°,四边形 BCDE是矩形,∴BE=CD=9.6 m,∠CDE=∠DEA=90°,∴∠ADC=90°+30°=120°.∵∠ACB=60°,∴∠ACD=30°,∴∠CAD=30°=∠ACD,∴AD=CD=
9.6 m.在Rt△ADE中,∠ADE=30°,∴AE=AD=4.8 m,∴AB=AE+BE=4.8+9.6=14.4(m).
16.(5-5) 【点拨】如图,过点D作DE⊥AC,垂足为E.依题意得,AB=20×
=10(海里),∠FAD=15°,∠FAC=45°,∠FAB=90°,∠ABC=45°,∴∠CAB=90°-45°=45°,∠DAC=
∠FAC-∠FAD=30°,∴∠ACB=180°-∠CAB-∠CBA=90°.在Rt△ACB中,AC=AB·sin 45°=10×=5(海里).设DE=x海里,在Rt△DAE中,AE===x(海里).∵DC∥AB,∴∠DCA=∠CAB=45°.在Rt△DEC中,CE==x海里,∴DC=x海里.∵AE+EC=AC,∴x+x=5,解得x=,∴DC=×=(5-5)海里.
三、17.解:(1)原式=+3-=3.
(2)原式=1+4××-=1+-(2-)=-1++.
18.解:∵∠C=90°,∠B=60°,
∴∠A=90°-∠B=90°-60°=30°.
∴BC=AC·tan A=15×=5.
∴AB=2BC=2×5=10.
19.解:在Rt△ABC中,AB=8米,∠ABC=37°,
∴AC=AB·sin∠ABC≈8×0.60=4.8(米),
BC=AB·cos∠ABC≈8×0.80=6.4(米).
在Rt△ADC中,∠ADC=30°,
∴CD=≈≈8.3(米),
∴BD=CD-BC≈8.3-6.4=1.9(米).
答:BD的长约为1.9米.
20.解:(1)如图,设BE=x,则EC=4-x,
∴AE=EC=4-x.
在Rt△ABE中,AB2+BE2=AE2,
∴(2)2+x2=(4-x)2,解得x=1.
∴BE=1,AE=CE=3.
∵AE=EC,∴∠1=∠2.
∵∠ABC=90°,∴∠CAB=90°-∠2,
∴∠CAB=90°-∠1.
由折叠可知△FAC≌△BAC,
∴∠FAC=∠CAB=90°-∠1,AF=AB=2 ,
∴∠FAC+∠1=90°,即∠FAE=90°.
在Rt△FAE中,EF===.
(2)如图,过F作FM⊥BC于M,
∴∠FME=∠FMC=90°.
设EM=a,则MC=3-a.
在Rt△FME中,FM2=FE2-EM2,
在Rt△FMC中,FM2=FC2-MC2,
∴FE2-EM2=FC2-MC2,
∴()2-a2=42-(3-a)2,∴a=.
∴EM=,∴FM== ,
∴sin∠CEF=== .
21.解:(1)∵AD=AC=2 m,∠AOD=90°,
∴CD=2OD.
在Rt△AOD中,∠OAD=α=65°,
∴OD=AD·sinα=2×sin 65°≈2×0.91=1.82(m),
∴CD=2OD≈3.6 m.
答:遮阳宽度CD约为3.6 m.
(2)如图,过点E作EH⊥AB于H,则∠BHE=90°.
∵AB⊥BF,EF⊥BF,∴∠ABF=∠EFB=90°,
∴四边形BFEH为矩形,∴EH=BF=3 m.
在Rt△AHE中,tanα=,∴AH=.
当α=65°时,AH=≈≈1.4(m),
当α=45°时,AH===3(m),
∴当α从65°减小到45°时,点E下降的高度约为3-1.4=1.6(m).
22.解:如图,过M点作ME⊥MN交CD于E点,则∠NME=90°.
由题易得四边形AMCB为矩形,
∴MC=AB=8 m,AB∥CM,
∴∠NMC=180°-∠BNM=180°-118°=62°.
∵地面上的点D经过平面镜MN反射后落在点C,
∴∠EMD=∠EMC=90°-∠NMC=90°-62°=28°,
∴∠CMD=56°.
在Rt△CMD中,tan∠CMD=,
即1.48≈,∴CD≈11.8 m.
即水平地面上最远处D到小强的距离CD约是11.8 m.
