沪科版第17章一元二次方程复习(1)
图片预览








文档简介
课件29张PPT。第17章一元二次方程复习(1)沪科版八年级(下册)第一关知识要点说一说1、一元二次方程的概念 只含有一个未知数,且未知数的最高次数是2的整式方程称为一元二次方程.2、一元二次方程的一般形式ax2+bx+c=0(a、b、c为常数,a≠0)a为二次项系数b为一次项系数 判别一个方程是一元二次方程的
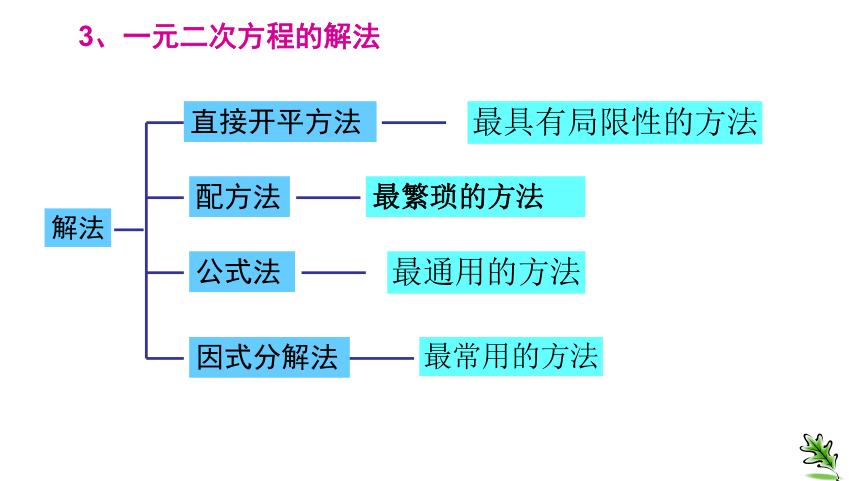
重要条件!解法3、一元二次方程的解法直接开平方法配方法公式法因式分解法最繁琐的方法一元二次方程判别式的情况4、一元二次方程根的判别式5、一元二次方程根与系数的关系第二关基础题目轮一轮1、(x-1)2=0 2、x2 = 84、ax2 + bx + c=13、x2 + =1 类型一:概念类问题其中是一元二次方程的有( )下列关于x的方程:A.4个 B.3个 C.2个 D.1个C例1若关于x的方程 是一元二次方程,
则a= 。点拨:由题意知a2-2=2且a-2≠0.
解得:a=-2-2类型一:概念类问题例2用适当的方法解下列方程例3(1) 2(x-1)2=32 解法一:(x-1)2=16
x-1=±4
∴x1=5,X2=-3解法二:(x-1)2-16=0
(x-1+4)(x-1-4)=0
x-5=0或x+3=0
∴x1=5,X2=-3因式分解法直接开平方法类型二:解法类问题(解方程) 用配方法的条件是:适应于任何一个一元二次方程,但是在没有特别要求的情况下,除了形如x2+2kx+c=0 (即二次项系数为1,一次项系数是偶数)用配方法外,一般不用 。(2) x2-4x-1=0 友情提示:配方法的一般步骤:二移----把常数项移到方程的右边;三配----把方程的左边配成一个完全平方式;四开----利用开平方法求出原方程的两个解.一除----把二次项系数化为1(方程的两边同时除以二次项系数a) 用公式法的条件是:适应于任何一个一元二次方程,先将方程化为一般形式,再求出b2-4ac的值, b2-4ac≥0则方程有实数根,b2-4ac<0 则方程无实数根。(3) 3x2+4x=2解:原方程可变形为
3x2+4x-2=0∵a=3,b=4,c=-2
∴b2-4ac=42+4×3×(-2)=40>0友情提示:类型三:解法类问题(根的判别式根与系数的关系)解:a=3,b=2,c=-9
△=b2-4ac=22-4×3×(-9)=112>0∴原方程有两个不相等的实数根. 不解方程,判别方程3x2+2x-9=0根的情况.例441例5第三关是对是错判一判案例1:
关于x的方程有两个不相等的实数根,又∵k-1≠0
∴k>0且k≠1忽视二次项
系数不为0求k的取值范围。案例2:
已知关于x的一元二次方程有两个实数根,求k的取值范围。又∵k+1≥0, ∴k≥-1∴k 的取值范围是k≥-1忽视题目中
的隐含条件解:由题意得案例3:
已知实数x满足求:代数式解:∵的值。忽视根的
存在条件!案例4:已知方程X2+kX+k+2=0的两个根是X1、X2,
且X12+X22 = 4,求k的值。 解:由根与系数的关系得:
X1+X2=-k, X1?X2=k+2
又 X12 + X2 2 = 4
即(X1+ X2)2 - 2 X1X2=4
∴ K2- 2(k+2)=4
∴ K2-2k-8=0
解得:k=4 或k=-2△ = 42-4(4+2) ∵ △= K2-4(k+2) 当k=4时,=16-24 <0当k=-2时,△ = (-2)2-4(-2+2) =4>0∴ k=-2第四关反败为胜选一选我选择 我喜欢 已知方程x2+kx = - 3? 的一个根是-1, 则k= , 另一根为______ 4x=-36若a为方程 的解,则 的值为 . 构造一个一元二次方程,要求:
(1)常数项为零(2)有一根为2。解方程:解方程: 将4个数a、b、c、d排成2行2列,两边各加一条竖线记成 m取什么值时,方程 x2+(2m+1)x+m2-4=0有两个相等的实数根?已知m为非负整数,且关于x的一元二次方程 :说明:当二次项系数也含有待定的字母时,要注意二次项系数不能为0,还要注意题目中待定字母的取值范围.解:∵方程有两个实数根∵m为非负整数∴m=0 或 m=1且m为非负整数有两个实数根,求m的值。 ∴ 你说我说大家说:
通过今天的学习你有什么收获或感受?谢谢同学们的合作
重要条件!解法3、一元二次方程的解法直接开平方法配方法公式法因式分解法最繁琐的方法一元二次方程判别式的情况4、一元二次方程根的判别式5、一元二次方程根与系数的关系第二关基础题目轮一轮1、(x-1)2=0 2、x2 = 84、ax2 + bx + c=13、x2 + =1 类型一:概念类问题其中是一元二次方程的有( )下列关于x的方程:A.4个 B.3个 C.2个 D.1个C例1若关于x的方程 是一元二次方程,
则a= 。点拨:由题意知a2-2=2且a-2≠0.
解得:a=-2-2类型一:概念类问题例2用适当的方法解下列方程例3(1) 2(x-1)2=32 解法一:(x-1)2=16
x-1=±4
∴x1=5,X2=-3解法二:(x-1)2-16=0
(x-1+4)(x-1-4)=0
x-5=0或x+3=0
∴x1=5,X2=-3因式分解法直接开平方法类型二:解法类问题(解方程) 用配方法的条件是:适应于任何一个一元二次方程,但是在没有特别要求的情况下,除了形如x2+2kx+c=0 (即二次项系数为1,一次项系数是偶数)用配方法外,一般不用 。(2) x2-4x-1=0 友情提示:配方法的一般步骤:二移----把常数项移到方程的右边;三配----把方程的左边配成一个完全平方式;四开----利用开平方法求出原方程的两个解.一除----把二次项系数化为1(方程的两边同时除以二次项系数a) 用公式法的条件是:适应于任何一个一元二次方程,先将方程化为一般形式,再求出b2-4ac的值, b2-4ac≥0则方程有实数根,b2-4ac<0 则方程无实数根。(3) 3x2+4x=2解:原方程可变形为
3x2+4x-2=0∵a=3,b=4,c=-2
∴b2-4ac=42+4×3×(-2)=40>0友情提示:类型三:解法类问题(根的判别式根与系数的关系)解:a=3,b=2,c=-9
△=b2-4ac=22-4×3×(-9)=112>0∴原方程有两个不相等的实数根. 不解方程,判别方程3x2+2x-9=0根的情况.例441例5第三关是对是错判一判案例1:
关于x的方程有两个不相等的实数根,又∵k-1≠0
∴k>0且k≠1忽视二次项
系数不为0求k的取值范围。案例2:
已知关于x的一元二次方程有两个实数根,求k的取值范围。又∵k+1≥0, ∴k≥-1∴k 的取值范围是k≥-1忽视题目中
的隐含条件解:由题意得案例3:
已知实数x满足求:代数式解:∵的值。忽视根的
存在条件!案例4:已知方程X2+kX+k+2=0的两个根是X1、X2,
且X12+X22 = 4,求k的值。 解:由根与系数的关系得:
X1+X2=-k, X1?X2=k+2
又 X12 + X2 2 = 4
即(X1+ X2)2 - 2 X1X2=4
∴ K2- 2(k+2)=4
∴ K2-2k-8=0
解得:k=4 或k=-2△ = 42-4(4+2) ∵ △= K2-4(k+2) 当k=4时,=16-24 <0当k=-2时,△ = (-2)2-4(-2+2) =4>0∴ k=-2第四关反败为胜选一选我选择 我喜欢 已知方程x2+kx = - 3? 的一个根是-1, 则k= , 另一根为______ 4x=-36若a为方程 的解,则 的值为 . 构造一个一元二次方程,要求:
(1)常数项为零(2)有一根为2。解方程:解方程: 将4个数a、b、c、d排成2行2列,两边各加一条竖线记成 m取什么值时,方程 x2+(2m+1)x+m2-4=0有两个相等的实数根?已知m为非负整数,且关于x的一元二次方程 :说明:当二次项系数也含有待定的字母时,要注意二次项系数不能为0,还要注意题目中待定字母的取值范围.解:∵方程有两个实数根∵m为非负整数∴m=0 或 m=1且m为非负整数有两个实数根,求m的值。 ∴ 你说我说大家说:
通过今天的学习你有什么收获或感受?谢谢同学们的合作
