2022—2023学年人教版数学八年级下册第十七章 勾股定理同步练习(含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册第十七章 勾股定理同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 213.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 08:28:33 | ||
图片预览


文档简介
人教版八年级数学下册
第十七章 勾股定理
一、选择题
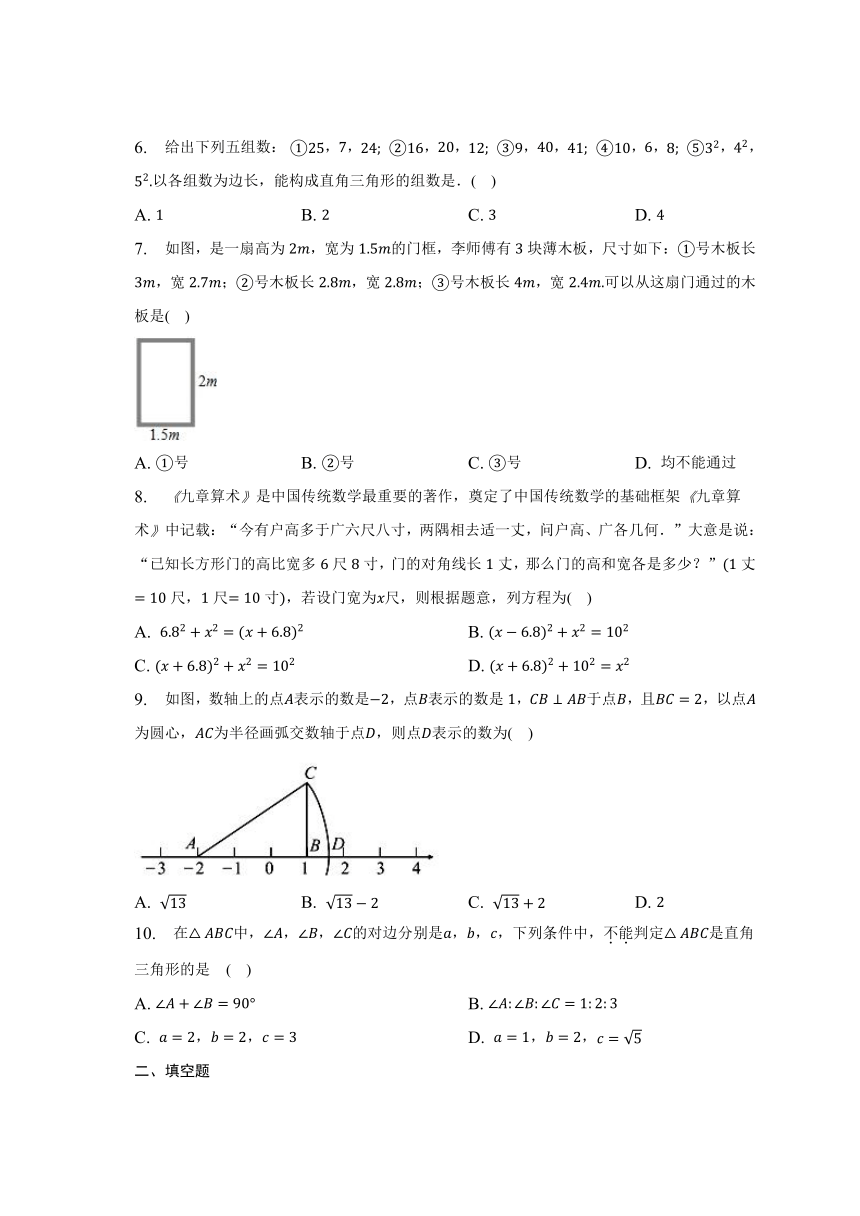
1. 在直角三角形中,若勾为,股为,则弦为( )
A. B. C. D.
2. 如图,长方形纸片中,,,将此长方形纸片折叠,使点与点重合,点落在点的位置,折痕为,则的面积为( )
A. B. C. D.
3. 下列说法中正确的是( )
A. 已知,,是三角形的三边,则
B. 在直角三角形中两边和的平方等于第三边的平方
C. 在中,,所以
D. 在中,,所以
4. 下列选项中,不能用来证明勾股定理的是( )
A. B. C. D.
5. 在中,、、分别是、、的对边,不能组成直角三角形的是( )
A. 三边之比:::: B. 三边长满足
C. 三角之比:::: D. 三边长满足
6. 给出下列五组数:,,,,,,,,,,以各组数为边长,能构成直角三角形的组数是.( )
A. B. C. D.
7. 如图,是一扇高为,宽为的门框,李师傅有块薄木板,尺寸如下:号木板长,宽;号木板长,宽;号木板长,宽可以从这扇门通过的木板是( )
A. 号 B. 号 C. 号 D. 均不能通过
8. 九章算术是中国传统数学最重要的著作,奠定了中国传统数学的基础框架九章算术中记载:“今有户高多于广六尺八寸,两隅相去适一丈,问户高、广各几何.”大意是说:“已知长方形门的高比宽多尺寸,门的对角线长丈,那么门的高和宽各是多少?”丈尺,尺寸,若设门宽为尺,则根据题意,列方程为( )
A. B.
C. D.
9. 如图,数轴上的点表示的数是,点表示的数是,于点,且,以点为圆心,为半径画弧交数轴于点,则点表示的数为( )
A. B. C. D.
10. 在中,,,的对边分别是,,,下列条件中,不能判定是直角三角形的是 ( )
A. B.
C. ,, D. ,,
二、填空题
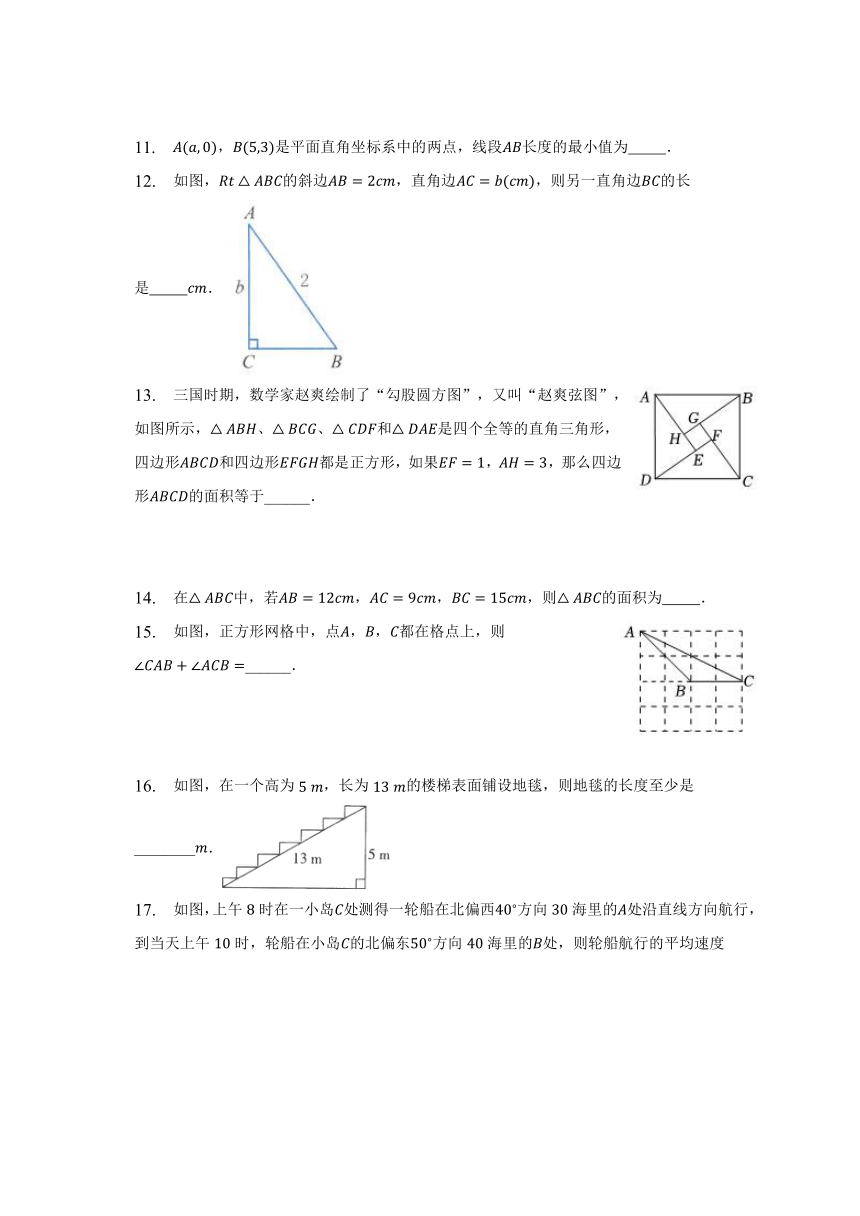
11. ,是平面直角坐标系中的两点,线段长度的最小值为 .
12. 如图,的斜边,直角边,则另一直角边的长是 .
13. 三国时期,数学家赵爽绘制了“勾股圆方图”,又叫“赵爽弦图”,如图所示,、、和是四个全等的直角三角形,四边形和四边形都是正方形,如果,,那么四边形的面积等于______.
14. 在中,若,,,则的面积为 .
15. 如图,正方形网格中,点,,都在格点上,则______.
16. 如图,在一个高为,长为的楼梯表面铺设地毯,则地毯的长度至少是________.
17. 如图,上午时在一小岛处测得一轮船在北偏西方向海里的处沿直线方向航行,到当天上午时,轮船在小岛的北偏东方向海里的处,则轮船航行的平均速度为 海里时.
18. 已知是的边上的高,若,,,则的长为______.
19. 在中,、、的对边分别是、、,且满足,则是 三角形.
20. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示“垂美”四边形,对角线,交于点,若,,则
三、解答题
21. 如图,在中,,,,是边上的高求:
的长
的面积
的长.
22. 如图,在正方形网格中,每个小正方形的边长都是,点,,,是网格线的交点.
求证:;
四边形的面积为______.
23. 如图,渔船在小岛的西南方向,距离小岛处.
渔船的位置应怎样表述
小岛的北偏东方向,距离小岛处是哪艘渔船
求渔船,之间的距离.
24. 如图,在四边形中,,,,求的长.
25. 如图,在四边形中,,,,,,求四边形的面积.
26. 如图,在正方形网格中画有一段笔直的铁路及道口,和村庄,完成以下作图.
若在村庄与道口之间修一条最短的公路,在图中画出此公路,并说明这样画的理由;
若在公路上选择一个地点安装实时监控系统,要求点到村庄与道口的距离相等,在图中标出点的位置;
当一节火车头行驶至铁路上的点时,距离村庄最近.在图中确定点的位置保留作图痕迹;
若在道口或处修建一座火车站,使得到两村的距离和较短,应该修在______处.
1、 ; 2、 ; 3、 ; 4、 ; 5、 ; 6、 ; 7、 ; 8、 ; 9、 ; 10、 ; 11、 ; 12、略 ; 13、 ; 14、 ; 15、 ; 16、 ; 17、 ; 18、或 ; 19、等腰直角 ; 20、
21、解:在中,,,,
.
在中,,,,
.
是边上的高.
.
.
.
22、证明:连接,
由题意得:,,,
,
是直角三角形,
;
解:如图:
由题意得:四边形的面积的面积的面积
,
故答案为:.
23、渔船在小岛的东南方向,距离小岛处;
渔船;
渔船在小岛的西南方向,渔船在小岛的东南方向,
,在中,
.
答:渔船,之间的距离.
24、解:,,
,
,
,
,
,
,
,
,
,
解得:或不符合题意,舍去,
的长为.
25、解:连接,如图所示:
,
为直角三角形,
又,,
根据勾股定理得:,
又,,
,,
,
为直角三角形,,
则.
26、
第十七章 勾股定理
一、选择题
1. 在直角三角形中,若勾为,股为,则弦为( )
A. B. C. D.
2. 如图,长方形纸片中,,,将此长方形纸片折叠,使点与点重合,点落在点的位置,折痕为,则的面积为( )
A. B. C. D.
3. 下列说法中正确的是( )
A. 已知,,是三角形的三边,则
B. 在直角三角形中两边和的平方等于第三边的平方
C. 在中,,所以
D. 在中,,所以
4. 下列选项中,不能用来证明勾股定理的是( )
A. B. C. D.
5. 在中,、、分别是、、的对边,不能组成直角三角形的是( )
A. 三边之比:::: B. 三边长满足
C. 三角之比:::: D. 三边长满足
6. 给出下列五组数:,,,,,,,,,,以各组数为边长,能构成直角三角形的组数是.( )
A. B. C. D.
7. 如图,是一扇高为,宽为的门框,李师傅有块薄木板,尺寸如下:号木板长,宽;号木板长,宽;号木板长,宽可以从这扇门通过的木板是( )
A. 号 B. 号 C. 号 D. 均不能通过
8. 九章算术是中国传统数学最重要的著作,奠定了中国传统数学的基础框架九章算术中记载:“今有户高多于广六尺八寸,两隅相去适一丈,问户高、广各几何.”大意是说:“已知长方形门的高比宽多尺寸,门的对角线长丈,那么门的高和宽各是多少?”丈尺,尺寸,若设门宽为尺,则根据题意,列方程为( )
A. B.
C. D.
9. 如图,数轴上的点表示的数是,点表示的数是,于点,且,以点为圆心,为半径画弧交数轴于点,则点表示的数为( )
A. B. C. D.
10. 在中,,,的对边分别是,,,下列条件中,不能判定是直角三角形的是 ( )
A. B.
C. ,, D. ,,
二、填空题
11. ,是平面直角坐标系中的两点,线段长度的最小值为 .
12. 如图,的斜边,直角边,则另一直角边的长是 .
13. 三国时期,数学家赵爽绘制了“勾股圆方图”,又叫“赵爽弦图”,如图所示,、、和是四个全等的直角三角形,四边形和四边形都是正方形,如果,,那么四边形的面积等于______.
14. 在中,若,,,则的面积为 .
15. 如图,正方形网格中,点,,都在格点上,则______.
16. 如图,在一个高为,长为的楼梯表面铺设地毯,则地毯的长度至少是________.
17. 如图,上午时在一小岛处测得一轮船在北偏西方向海里的处沿直线方向航行,到当天上午时,轮船在小岛的北偏东方向海里的处,则轮船航行的平均速度为 海里时.
18. 已知是的边上的高,若,,,则的长为______.
19. 在中,、、的对边分别是、、,且满足,则是 三角形.
20. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示“垂美”四边形,对角线,交于点,若,,则
三、解答题
21. 如图,在中,,,,是边上的高求:
的长
的面积
的长.
22. 如图,在正方形网格中,每个小正方形的边长都是,点,,,是网格线的交点.
求证:;
四边形的面积为______.
23. 如图,渔船在小岛的西南方向,距离小岛处.
渔船的位置应怎样表述
小岛的北偏东方向,距离小岛处是哪艘渔船
求渔船,之间的距离.
24. 如图,在四边形中,,,,求的长.
25. 如图,在四边形中,,,,,,求四边形的面积.
26. 如图,在正方形网格中画有一段笔直的铁路及道口,和村庄,完成以下作图.
若在村庄与道口之间修一条最短的公路,在图中画出此公路,并说明这样画的理由;
若在公路上选择一个地点安装实时监控系统,要求点到村庄与道口的距离相等,在图中标出点的位置;
当一节火车头行驶至铁路上的点时,距离村庄最近.在图中确定点的位置保留作图痕迹;
若在道口或处修建一座火车站,使得到两村的距离和较短,应该修在______处.
1、 ; 2、 ; 3、 ; 4、 ; 5、 ; 6、 ; 7、 ; 8、 ; 9、 ; 10、 ; 11、 ; 12、略 ; 13、 ; 14、 ; 15、 ; 16、 ; 17、 ; 18、或 ; 19、等腰直角 ; 20、
21、解:在中,,,,
.
在中,,,,
.
是边上的高.
.
.
.
22、证明:连接,
由题意得:,,,
,
是直角三角形,
;
解:如图:
由题意得:四边形的面积的面积的面积
,
故答案为:.
23、渔船在小岛的东南方向,距离小岛处;
渔船;
渔船在小岛的西南方向,渔船在小岛的东南方向,
,在中,
.
答:渔船,之间的距离.
24、解:,,
,
,
,
,
,
,
,
,
,
解得:或不符合题意,舍去,
的长为.
25、解:连接,如图所示:
,
为直角三角形,
又,,
根据勾股定理得:,
又,,
,,
,
为直角三角形,,
则.
26、
