14.9圆的内接四边形[下学期]

课件14张PPT。复习导入１、（１）如图１，在⊙O上任取三点A、B、C，连结AB、BC、CA，则△ABC叫做⊙O的______三角形，⊙O叫做△ABC的________圆。（２）图１中的∠A、∠B、∠C都是⊙O的______角，若∠A＝42°，则　　＝　　°，　　＝　　°。276内接外接圆周842、如图，点A、B、C、D在⊙O上，
若优弧ABC为2600，则∠D=__
若弧AC为100o则∠B=__，∠B+ ∠D=__,
∠A+ ∠C=___
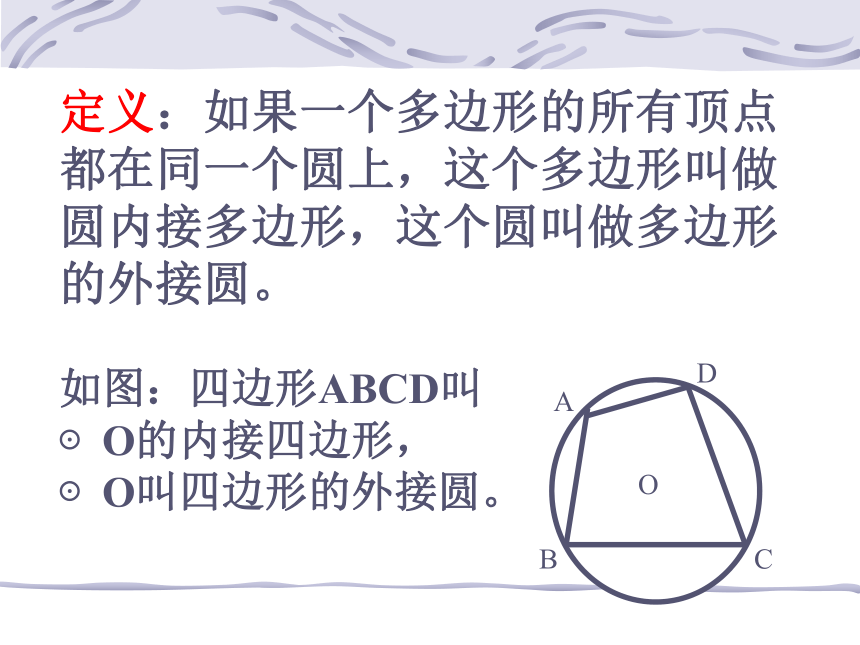
14、9 圆内接四边形定义：如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做多边形的外接圆。ABCDO如图：四边形ABCD叫⊙O的内接四边形，⊙O叫四边形的外接圆。观察与思考（1）左图中，∠A+∠C=?; ∠B+∠D=?
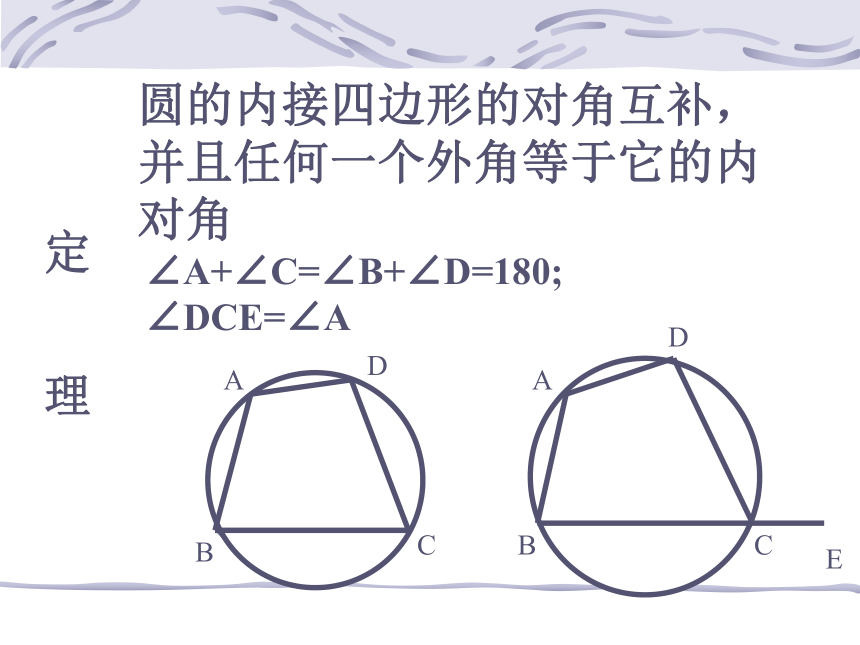
（2）右图中，∠DCE和∠A有什么关系？ABCDBCDAE定 理圆的内接四边形的对角互补，并且任何一个外角等于它的内对角ABCDABCED∠A+∠C=∠B+∠D=180; ∠DCE=∠A
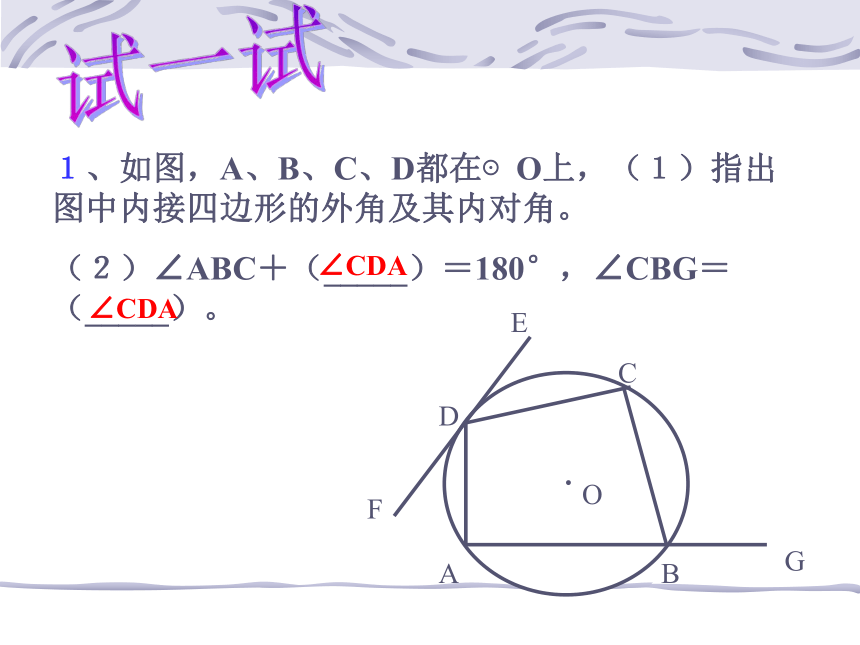
１、如图，A、B、C、D都在⊙O上，（１）指出图中内接四边形的外角及其内对角。
（２）∠ABC＋（_____）＝180°，∠CBG＝（_____）。试一试∠CDA∠CDA２、如图，四边形ABCD为⊙O的内接四边形，已知∠BOD为100°，求∠BAD和∠BCD的度数。例题演练如图，AD是△ABC外角∠EAC的平分线，与三角形的外接圆交于点D。求证：DB=DCEABCD新知应用
已知：如图，⊙O１和⊙O２相交于A、B两点，经过点A的直线CD与⊙O１交于点C，与⊙O２交于点D，经过点B的直线EF与⊙O１交于点E，与⊙O２交于点F。
求证：CE∥DF如果图形有如下变化，上题的结论CE∥DF还成立吗？怎样证明？变 式 练 习ABCDEF还可能有其他的图形变化吗？
请同学们课后
思考。圆内接四边形的性质定理：
（1）对角互补
（2）任何一个外角都等于内对角辅助线的作法：
如果两圆相交，则连接两圆的公共弦。本课小结例题演练如图，⊙M和⊙N都经过A,B两点，过B作直线分别交两圆于C,D，G为圆外一点，GC交⊙M于E,交 ⊙N于F。 求证：∠GEA+∠GFA=180°GCDBAEF作业布置：
（1）作业本
（2）自主训练