切割线定理[下学期]

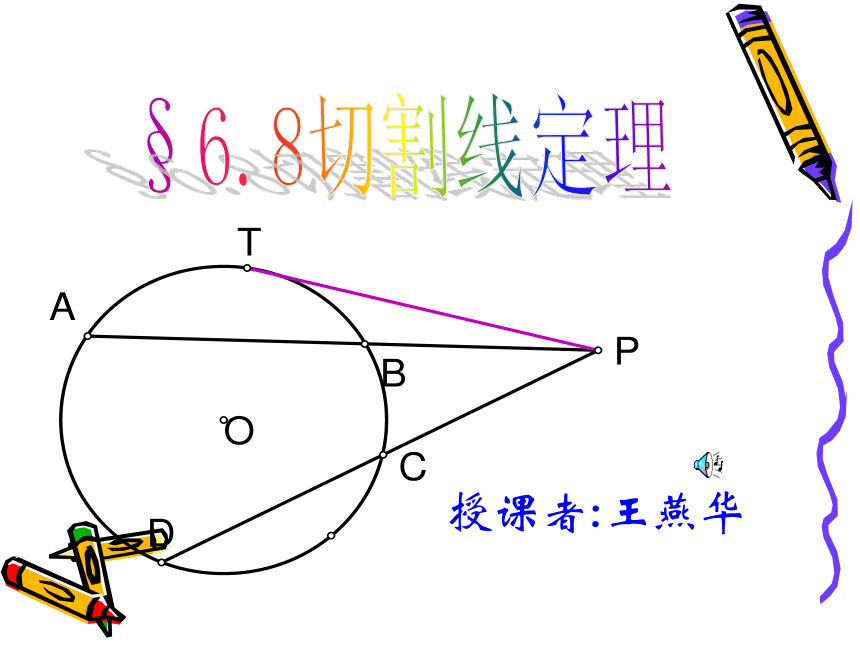
课件17张PPT。§6.8切割线定理授课者:王燕华诗人借着登鹳鹊楼,来描述景色的状观,以及抒发自己对人生的理想,包涵着自我提升的寓意,登高始能望远,想有所获,就应努力提高自己!如果真的能看一千里,那么楼应该建多高呢?你猜猜看?我们能不能用数学知识来
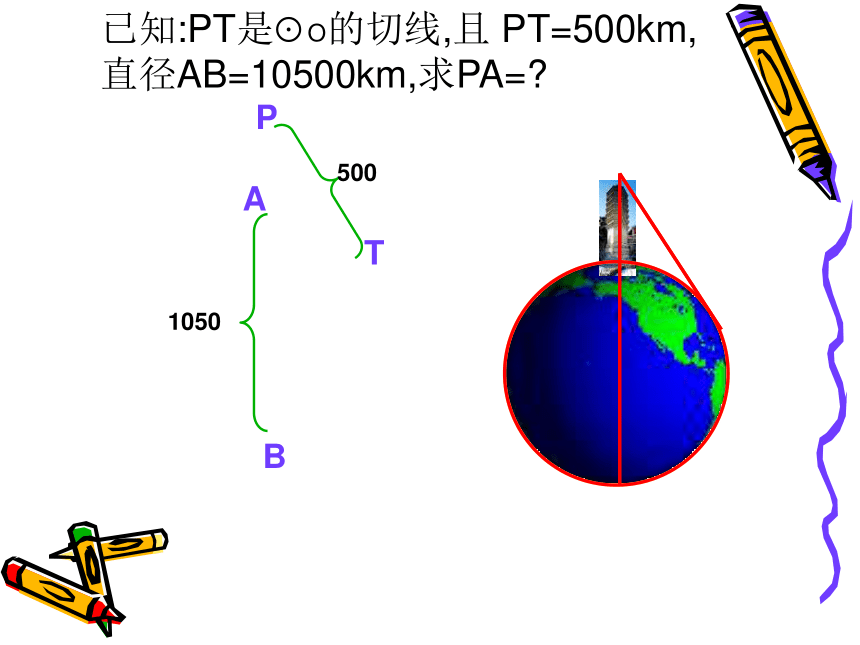
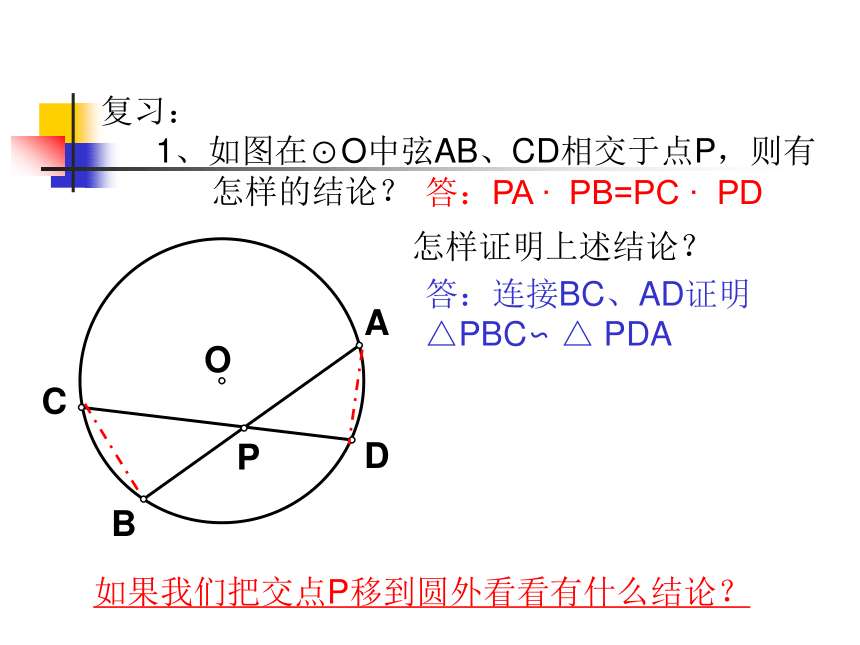
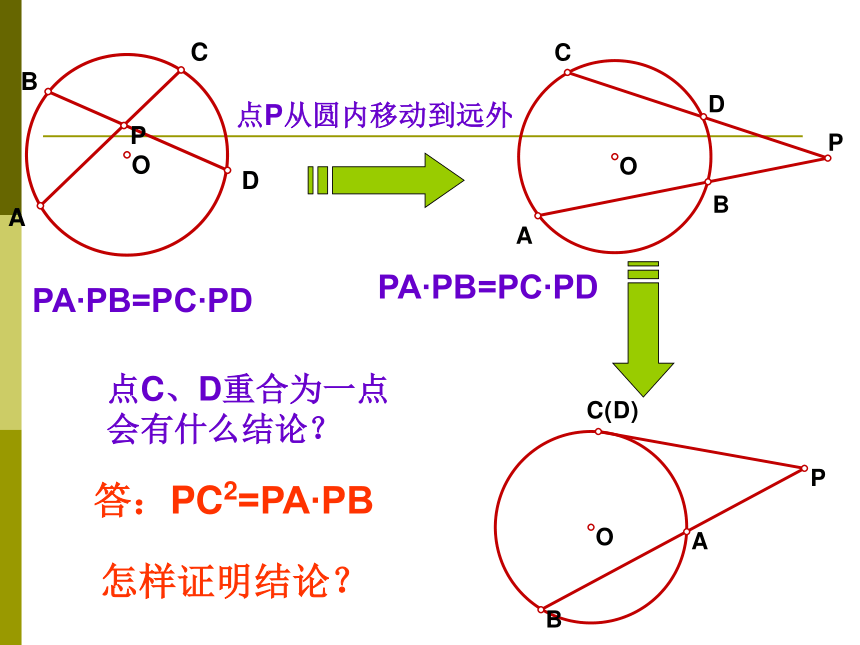
解决这个问题呢?PTAB5001050答：PA ? PB=PC ? PD怎样证明上述结论？答：连接BC、AD证明
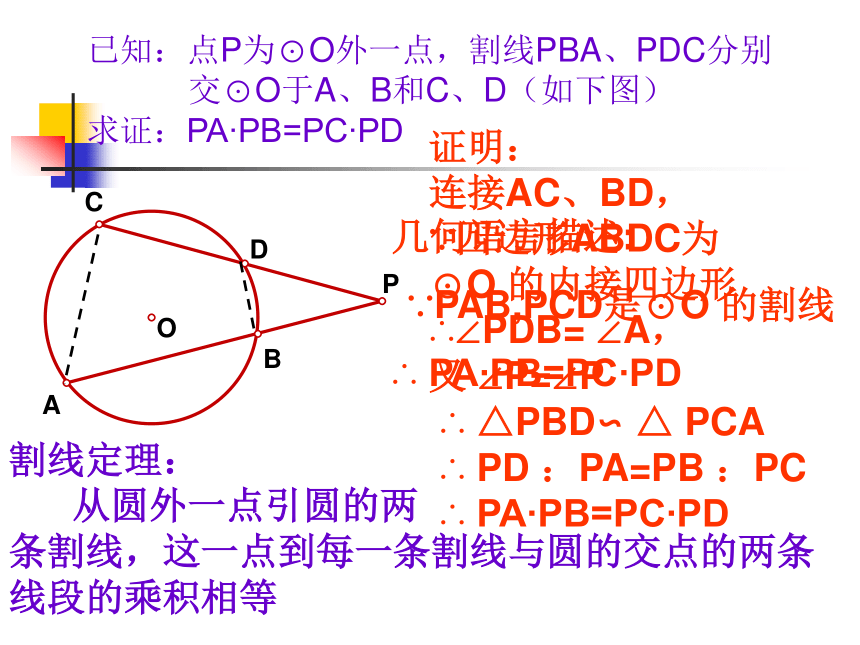
△PBC∽ △ PDA 如果我们把交点P移到圆外看看有什么结论？已知：点P为⊙O外一点，割线PBA、PDC分别
交⊙O于A、B和C、D（如下图）
求证：PA?PB=PC?PD证明：
连接AC、BD，
∵四边形ABDC为
⊙O 的内接四边形
∴∠PDB= ∠A，
又 ∠P=∠P
∴ △PBD∽ △ PCA
∴ PD ：PA=PB ：PC
∴ PA?PB=PC?PD割线定理：
从圆外一点引圆的两
条割线，这一点到每一条割线与圆的交点的两条
线段的乘积相等几何语言描述:
∵PAB,PCD是⊙O 的割线
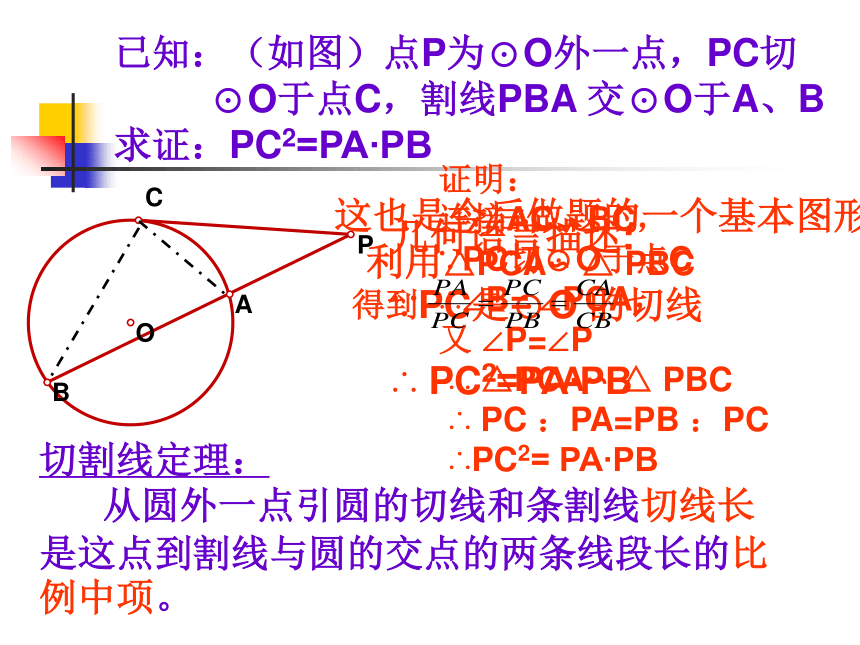
∴ PA?PB=PC?PD点C、D重合为一点会有什么结论？答：PC2=PA?PB怎样证明结论？证明：
连接AC、BC，
∵PC切⊙O于点C
∴∠B= ∠PCA，
又 ∠P=∠P
∴ △PCA∽ △ PBC
∴ PC ：PA=PB ：PC
∴PC2= PA?PB切割线定理：
从圆外一点引圆的切线和条割线切线长是这点到割线与圆的交点的两条线段长的比例中项。几何语言描述:
∵PC是⊙O 的切线
∴ PC2=PA?PBAB交CD于点
=> PA?PB=PC?PDPC切⊙O于点C点
=> PA?PB=PC2割线PCD、PAB交⊙O于点C、D和A、B
=> PA?PB=PC?PD思考：从这几个定理的结论里
大家能发现什么共同点？结论都为乘积式几条线段都是从同一点出发都是通过三角形相似来证明
（都隐含着三角形相似）我们学过的定理中还有结论
为乘积式的吗？TABPO这也是今后做题的一个基本图形∵PＴ是⊙O 的切线
∴ PＴ2=PA?PB(x+1250)(x-200) =0x=200或x=-1250(舍去）设PA＝x，则5002=x(x+1050)1.如图,割线PAB,PCD分别交圆于A,B和C,D
(1)已知PB=5,PA=8,PC=4,
PD= PT=
(2)已知PA=5,PB=8,PO=7
半径R=
2.如图,割线PAB,PCD分别交圆于A,B和C,D,连结AC,BD,下面各比例式中成立的有:
(1) (2) (3)小试身手：103 解：（1）由切割线定理，得
PC ? PD=PA ? PB解得： （ 负数不合题意，舍去）∵AB=3cm,PA=2cm
∴PB=AB+PA=5（cm）∵CD=4cm ∴PD=PC+CD=PC+4
∴PC（PC+4）=2X5化简，整理得：PC2+4PC?10=0由(1)得PE2=PA?PB=10由弦切角定理,得∠CEP=∠D又∵ ∠CPE=∠EPD∴△CPE∽△EPD分析：要证明PB ：PD=PO ：PC 很明显PB、PD、PO、PC在同一直线上无法直接用相似证明，且在圆里的比例线段通常化为乘积式来证明，所以可以通过证明PB ? PC=PD ? PO,而由切割线定理有PA2=PB ? PC只需再证PA2=PD ? PO，PA为切线所以连接PO由射影定理 得到。大展才干：课堂小结1、这节课我们学习了切割线定理及推论（割线定理），
要特别注意它与相交弦定理之间的联系与区别。2、要注意圆中的比例线段的结论的特点及实际中的用。3、圆中的比例线段在实际应用中也非常重要，注意与
代数、几何等知识的联系及应用谢谢光临指导