7.1平面直角坐标系同步练习题 (含答案)2022-2023学年人教版七年级数学下册
文档属性
| 名称 | 7.1平面直角坐标系同步练习题 (含答案)2022-2023学年人教版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 477.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 10:24:46 | ||
图片预览



文档简介
7.1 平面直角坐标系 同步练习题
一、单选题 (本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在平面直角坐标系中,点在第二象限,并且到轴和轴的距离分别是3和2,则点坐标为( )
A. B. C. D.
2.如图,所有正方形的中心均在坐标原点,且各边与轴或轴平行,从内到外,它们的边长依次为,,,,,…,顶点,,,,,的坐标分别为,,,,,,,则顶点的坐标是( )
A. B. C. D.
3.小明的家在学校正南,正东方向处,如果以学校位置为原点,以正东、正北为正方向,则小明家用有序数对表示为( )
A. B. C. D.
4.3排5号用有序数对表示,则4排2号可以表示为( )
A. B. C. D.
5.不论m取何实数,点都不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.若点P在x轴的下方,y轴的右侧,到y轴的距离是3,到x轴的距离是5,则点P的坐标为( )
A.(﹣3,5) B.(﹣5,3) C.(3,﹣5) D.(5,﹣3)
7.定义:直线与相交于点,对于平面内任意一点,点到直线,的距离分别为,,则称有序非负实数对是点的“距离坐标”根据上述定义,“距离坐标”是的点的个数是( )
A. B. C. D.
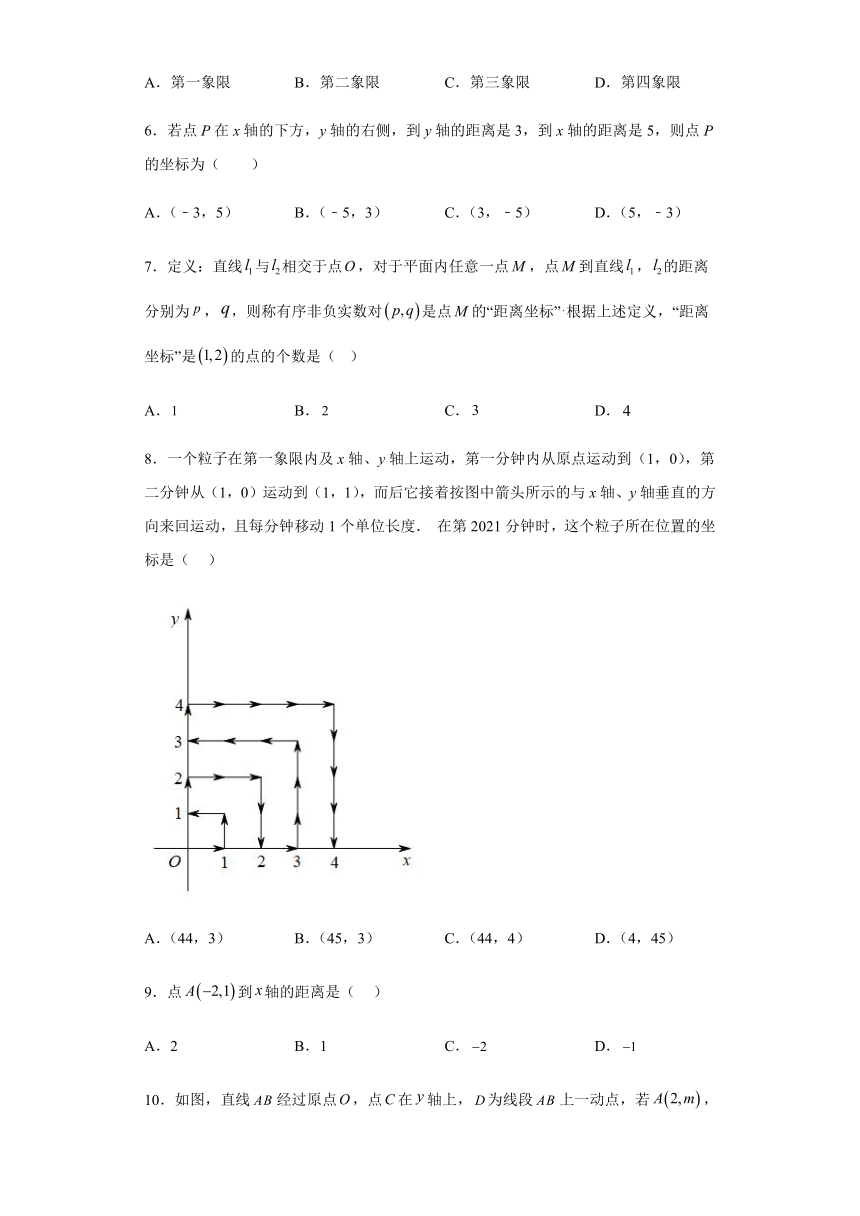
8.一个粒子在第一象限内及x轴、y轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x轴、y轴垂直的方向来回运动,且每分钟移动1个单位长度. 在第2021分钟时,这个粒子所在位置的坐标是( )
A.(44,3) B.(45,3) C.(44,4) D.(4,45)
9.点到轴的距离是( )
A.2 B.1 C. D.
10.如图,直线经过原点,点在轴上,为线段上一动点,若,,,,则长度的最小值为( )
A.1 B.2 C. D.
二、填空题(本题共6小题,每小题4分,共24分)
11.在平面直角坐标系中,,如果在y轴上存在一点P,使得的面积与的面积相等,则点P的坐标为 __.
12.已知点在一、三象限的角平分线上,则______.
13.点在轴的下方,且距离轴3个单位长度,距离轴4个单位长度,那么点的坐标是________.
14.已知点A,B的坐标分别为和,若轴,则___________.
15.若,则点在第_________象限.
16.在如图所示的平面直角坐标系中,一只蚂蚁从 A 点出发,沿着循环爬行,其中 A 点坐标为, B 的坐标为,C 的坐标为,D 的坐标 为,当蚂蚁爬了 2015 个单位时,它所处位置的坐标为______________.
三、解答题 本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.18-21题 每题8分 22题10分 23题10分 24题13分 25题13分
17.(1)计算:.
(2)已知点是平面直角坐标系中第四象限内的点,化简.
18.已知点,若满足,则称点P为“新奇点”.若点是“新奇点”,请判断点M在第几象限?并说明理由.
19.在平面直角坐标系中,已知点,点P在过点,且与x轴平行的直线上,求出点P的坐标.
20.正方形ABCD的边长为4,请你建立适当的平面直角坐标系,写出各个顶点的坐标.
21.如图,在△AOB中,A、B两点的坐标分别为(2,4)和(6,2),求△AOB的面积
22.已知:如图,正方形ABCD的边长为8,如果以A点为原点,AB所在直线为x轴,写出正方形各顶点的坐标.
23.在平面直角坐标系中描出下列两组的点,并用线段顺次连接起来:
(1)(-9,0),(-9,3),(-10,3),(-6,5),(-2,3),(-3,3),(-3,0);
(2)(3,0),(3,3),(0,3),(2,5),(1,5),(3,7),(2,7),(3.5,9),(5,7),(4,7),(6,5),(5,5),(7,3),(4,3),(4,0)
这幅图画,你们觉得它像什么?
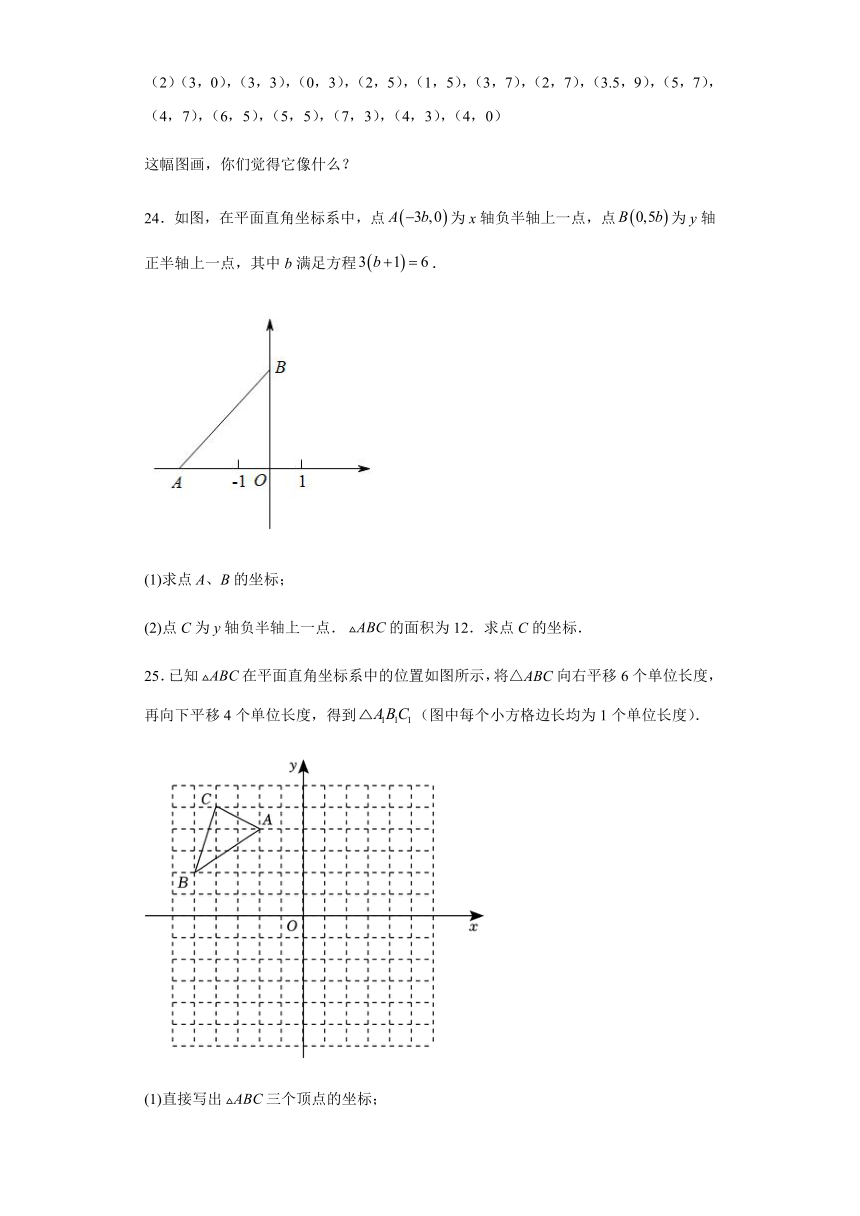
24.如图,在平面直角坐标系中,点为x轴负半轴上一点,点为y轴正半轴上一点,其中b满足方程.
(1)求点A、B的坐标;
(2)点C为y轴负半轴上一点.的面积为12.求点C的坐标.
25.已知在平面直角坐标系中的位置如图所示,将△ABC向右平移6个单位长度,再向下平移4个单位长度,得到(图中每个小方格边长均为1个单位长度).
(1)直接写出三个顶点的坐标;
(2)在图中画出平移后的;
(3)直接写出三个顶点的坐标;
(4)求的面积.
参考答案:
1.D
2.D
3.C
4.A
5.C
6.C
7.D
8.A
9.B
10.A
11.或
12.5
13.或
14.
15.四
16.(1,0)
17.(1);
(2)
【详解】解:(1)原式;
(2)∵点在第四象限,
∴,,
∴
.
18.点M在第三象限,见解析
【详解】解:点M在第三象限,理由如下:
∵点是“新奇点”,
∴,解得,
∴,,
∴点M在第三象限.
19.
【详解】解:由题意得,,
解得,
∴,
则点P的坐标为.
20.见解析
【详解】可以以正方形中互相垂直的边所在的直线为坐标轴,建立平面直角坐标系,再根据点的位置和线段长表示坐标.
解:(这是开放题,答案不唯一)以AB所在的直线为x轴,AD所在的直线为y轴,并以点A为坐标原点,建立平面直角坐标系如图所示,
则点A、B、C、D的坐标分别是(0,0)、(4,0)、(4,4)、(0,4).
21.10
【详解】如图,过A作水平线l交y轴于点E,过B作垂线,交直线l与点C,交x轴于点D,则
S矩形ECDO=6×4=24,
SRt△AEO=×4×2=4;
SRt△ABC==4;
SRt△OBD=×6×2=6;
∴S△OAB=S矩形ECDO﹣SRt△ABC﹣SRt△AEO﹣SRt△OBD=10.
∴三角形AOB的面积是10.
22.A(0,0)、B(8,0)、C(8,8)、D(0,8).
详解:
按题中要求建立平面直角坐标系如下图所示:
∵四边形ABCD为正方形,边长为8,点A与坐标原点重合,AB边与x轴重合,
∴OB=BC=CD=AD=8,∠CDO=∠BCD=∠OBC=90°,
∴CB⊥x轴,CD⊥y轴,
∴点A、B、C、D的坐标分别为(0,0)、(8,0)、(8,8),(0,8).
作图见解析;
【详解】解:作图如下.
这幅图画像一栋“房子”旁边还有一棵“大树”,其中,第(1)组点连成一栋“房子”,第(2)组点连成一棵“大树”.
24.(1),
(2)
【详解】(1)解:解方程,得到,
,
∴,.
(2)解:由题意,设点的坐标为,
,
,
的面积为12,
,即,
解得,
则点的坐标为.
25.(1)
(2)见解析
(3)
(4)
【详解】(1);
(2)如图所示;
(3)由图可知,;
(4)
.
一、单选题 (本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在平面直角坐标系中,点在第二象限,并且到轴和轴的距离分别是3和2,则点坐标为( )
A. B. C. D.
2.如图,所有正方形的中心均在坐标原点,且各边与轴或轴平行,从内到外,它们的边长依次为,,,,,…,顶点,,,,,的坐标分别为,,,,,,,则顶点的坐标是( )
A. B. C. D.
3.小明的家在学校正南,正东方向处,如果以学校位置为原点,以正东、正北为正方向,则小明家用有序数对表示为( )
A. B. C. D.
4.3排5号用有序数对表示,则4排2号可以表示为( )
A. B. C. D.
5.不论m取何实数,点都不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.若点P在x轴的下方,y轴的右侧,到y轴的距离是3,到x轴的距离是5,则点P的坐标为( )
A.(﹣3,5) B.(﹣5,3) C.(3,﹣5) D.(5,﹣3)
7.定义:直线与相交于点,对于平面内任意一点,点到直线,的距离分别为,,则称有序非负实数对是点的“距离坐标”根据上述定义,“距离坐标”是的点的个数是( )
A. B. C. D.
8.一个粒子在第一象限内及x轴、y轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x轴、y轴垂直的方向来回运动,且每分钟移动1个单位长度. 在第2021分钟时,这个粒子所在位置的坐标是( )
A.(44,3) B.(45,3) C.(44,4) D.(4,45)
9.点到轴的距离是( )
A.2 B.1 C. D.
10.如图,直线经过原点,点在轴上,为线段上一动点,若,,,,则长度的最小值为( )
A.1 B.2 C. D.
二、填空题(本题共6小题,每小题4分,共24分)
11.在平面直角坐标系中,,如果在y轴上存在一点P,使得的面积与的面积相等,则点P的坐标为 __.
12.已知点在一、三象限的角平分线上,则______.
13.点在轴的下方,且距离轴3个单位长度,距离轴4个单位长度,那么点的坐标是________.
14.已知点A,B的坐标分别为和,若轴,则___________.
15.若,则点在第_________象限.
16.在如图所示的平面直角坐标系中,一只蚂蚁从 A 点出发,沿着循环爬行,其中 A 点坐标为, B 的坐标为,C 的坐标为,D 的坐标 为,当蚂蚁爬了 2015 个单位时,它所处位置的坐标为______________.
三、解答题 本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.18-21题 每题8分 22题10分 23题10分 24题13分 25题13分
17.(1)计算:.
(2)已知点是平面直角坐标系中第四象限内的点,化简.
18.已知点,若满足,则称点P为“新奇点”.若点是“新奇点”,请判断点M在第几象限?并说明理由.
19.在平面直角坐标系中,已知点,点P在过点,且与x轴平行的直线上,求出点P的坐标.
20.正方形ABCD的边长为4,请你建立适当的平面直角坐标系,写出各个顶点的坐标.
21.如图,在△AOB中,A、B两点的坐标分别为(2,4)和(6,2),求△AOB的面积
22.已知:如图,正方形ABCD的边长为8,如果以A点为原点,AB所在直线为x轴,写出正方形各顶点的坐标.
23.在平面直角坐标系中描出下列两组的点,并用线段顺次连接起来:
(1)(-9,0),(-9,3),(-10,3),(-6,5),(-2,3),(-3,3),(-3,0);
(2)(3,0),(3,3),(0,3),(2,5),(1,5),(3,7),(2,7),(3.5,9),(5,7),(4,7),(6,5),(5,5),(7,3),(4,3),(4,0)
这幅图画,你们觉得它像什么?
24.如图,在平面直角坐标系中,点为x轴负半轴上一点,点为y轴正半轴上一点,其中b满足方程.
(1)求点A、B的坐标;
(2)点C为y轴负半轴上一点.的面积为12.求点C的坐标.
25.已知在平面直角坐标系中的位置如图所示,将△ABC向右平移6个单位长度,再向下平移4个单位长度,得到(图中每个小方格边长均为1个单位长度).
(1)直接写出三个顶点的坐标;
(2)在图中画出平移后的;
(3)直接写出三个顶点的坐标;
(4)求的面积.
参考答案:
1.D
2.D
3.C
4.A
5.C
6.C
7.D
8.A
9.B
10.A
11.或
12.5
13.或
14.
15.四
16.(1,0)
17.(1);
(2)
【详解】解:(1)原式;
(2)∵点在第四象限,
∴,,
∴
.
18.点M在第三象限,见解析
【详解】解:点M在第三象限,理由如下:
∵点是“新奇点”,
∴,解得,
∴,,
∴点M在第三象限.
19.
【详解】解:由题意得,,
解得,
∴,
则点P的坐标为.
20.见解析
【详解】可以以正方形中互相垂直的边所在的直线为坐标轴,建立平面直角坐标系,再根据点的位置和线段长表示坐标.
解:(这是开放题,答案不唯一)以AB所在的直线为x轴,AD所在的直线为y轴,并以点A为坐标原点,建立平面直角坐标系如图所示,
则点A、B、C、D的坐标分别是(0,0)、(4,0)、(4,4)、(0,4).
21.10
【详解】如图,过A作水平线l交y轴于点E,过B作垂线,交直线l与点C,交x轴于点D,则
S矩形ECDO=6×4=24,
SRt△AEO=×4×2=4;
SRt△ABC==4;
SRt△OBD=×6×2=6;
∴S△OAB=S矩形ECDO﹣SRt△ABC﹣SRt△AEO﹣SRt△OBD=10.
∴三角形AOB的面积是10.
22.A(0,0)、B(8,0)、C(8,8)、D(0,8).
详解:
按题中要求建立平面直角坐标系如下图所示:
∵四边形ABCD为正方形,边长为8,点A与坐标原点重合,AB边与x轴重合,
∴OB=BC=CD=AD=8,∠CDO=∠BCD=∠OBC=90°,
∴CB⊥x轴,CD⊥y轴,
∴点A、B、C、D的坐标分别为(0,0)、(8,0)、(8,8),(0,8).
作图见解析;
【详解】解:作图如下.
这幅图画像一栋“房子”旁边还有一棵“大树”,其中,第(1)组点连成一栋“房子”,第(2)组点连成一棵“大树”.
24.(1),
(2)
【详解】(1)解:解方程,得到,
,
∴,.
(2)解:由题意,设点的坐标为,
,
,
的面积为12,
,即,
解得,
则点的坐标为.
25.(1)
(2)见解析
(3)
(4)
【详解】(1);
(2)如图所示;
(3)由图可知,;
(4)
.
