2022-2023学年京改版九年级数学下册23.3轴对称变换同步练习(无答案)
文档属性
| 名称 | 2022-2023学年京改版九年级数学下册23.3轴对称变换同步练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 418.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 11:07:04 | ||
图片预览



文档简介
京改版九年级数学下册23.3轴对称变换同步练习
一、单选题
1、如图,在平面直角坐标系中,△ABC位于第二象限,点B的坐标是(﹣5,2),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于于x轴对称的△A2B2C2,则点B的对应点B2的坐标是( )
A.(﹣3,2) B.(2,﹣3) C.(1,2) D.(﹣1,﹣2)
2、如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下,这样剪得的△ADH中 ( )
A.AH=DH≠AD B.AH=DH=AD C.AH=AD≠DH D.AH≠DH≠AD
3、如图,直线a,b相交于点O,P为这两直线外一点,且OP=1.7,若点关于直线a,b的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )
A.0 B.3 C.4 D.5
4、定义:在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径,点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即或或等,则点P关于极轴对称的点Q的极坐标表示不正确的是( )
A. B. C. D.
5、如图,,C为OB上的定点,M,N分别为射线OA、OB上的动点.当的值最小时,的度数为( )
A. B. C. D.
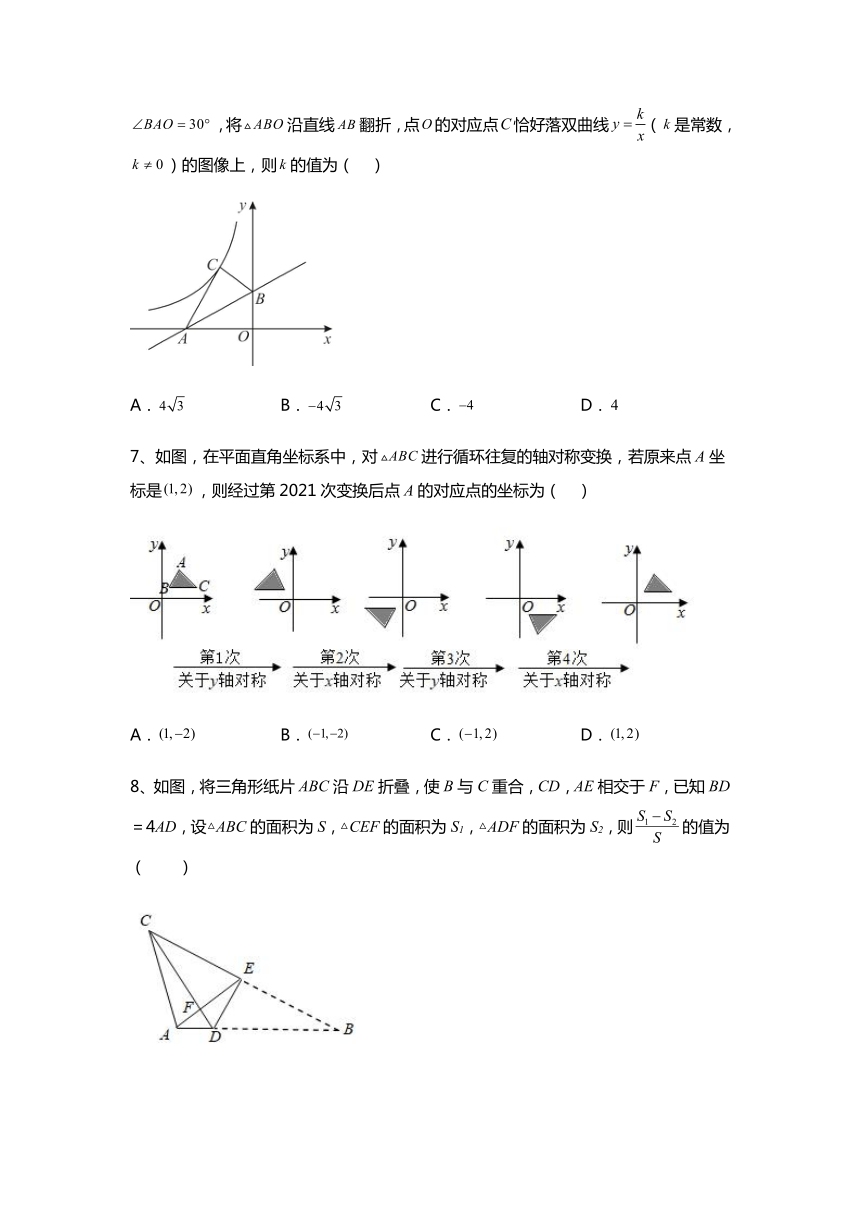
6、如图,在平面直角坐标系中,直线与轴、轴分别相交于点、.,,将沿直线翻折,点的对应点恰好落双曲线(是常数,)的图像上,则的值为( )
A. B. C. D.
7、如图,在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点A坐标是,则经过第2021次变换后点A的对应点的坐标为( )
A. B. C. D.
8、如图,将三角形纸片ABC沿DE折叠,使B与C重合,CD,AE相交于F,已知BD=4AD,设△ABC的面积为S,△CEF的面积为S1,△ADF的面积为S2,则的值为( )
A. B. C. D.
二、填空题
1、已知点,若点M关于x轴的对称点在第三象限,则a的取值范围是______.
2、如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、,若CD//BE,,则的度数是________.
3、仔细观察图1,体会图1的几何意义.用图1的方法和结论操作一长方形纸片得图2或图3或······,OC,OD均是折痕,当B'在∠COA'的内部时,连接OB',若∠AOC=44°,∠BOD=61°,∠A'OB'的度数是___________.
4、如图,在平面直角坐标系中,点A的坐标是,点B的坐标是,在y轴和x轴上分别有两点P、Q,则A,B,P,Q四点组成的四边形的最小周长为__.
5、如图,是内一定点,点,分别在边,上运动,若,,则的周长的最小值为___________.
6、在平面直角坐标系中,点与点关于x轴对称,则的值是______.
三、解答题
1、作图计算题.如图,在正方形网格上有一个(三个顶点均在格点上,网格上的最小正方形的边长为1).
(1)作关于直线的轴对称图形(不写作法);
(2)画出中边上的高;
(3)画一个锐角(要求各顶点在格点上),使其面积等于的面积.
(4)在HG上画出点,使最小.
2、如图,三个顶点的坐标分别是,,.
(1)试画出关于轴对称的,并写出、、的坐标;
(2)在轴上求作一点,使周长最小,试画出,直接写出点的坐标.
3、如图,在三角形纸片ABC中,AB=12,BC=7,AC=9,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,求△AED的周长.
4、在平面直角坐标系中,的三个顶点的位置如图所示.
(1)请画出关于轴对称的;
(2)直接写出关于轴对称的的,,三点的坐标:__________,__________,__________;
(3)求的面积.
5、如图,是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,,,在边上取一点D,将纸片沿翻折,使点O落在边上的点E处.
(1)求的长;
(2)求D,E两点的坐标.
6、如图,长方形,点E是上的一点,将沿折叠后得到,且点O在长方形内部.已知,.
(1)如图1,若,求四边形的面积.
(2)如图2,延长交于F,连结,将沿折叠,当点D的对称点恰好为点O时,求四边形的面积.
(3)如图3,在(2)的条件下,延长交于点G,连结,将沿折叠,当点C的对称点恰好为点O时,求四边形的面积.
一、单选题
1、如图,在平面直角坐标系中,△ABC位于第二象限,点B的坐标是(﹣5,2),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于于x轴对称的△A2B2C2,则点B的对应点B2的坐标是( )
A.(﹣3,2) B.(2,﹣3) C.(1,2) D.(﹣1,﹣2)
2、如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下,这样剪得的△ADH中 ( )
A.AH=DH≠AD B.AH=DH=AD C.AH=AD≠DH D.AH≠DH≠AD
3、如图,直线a,b相交于点O,P为这两直线外一点,且OP=1.7,若点关于直线a,b的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )
A.0 B.3 C.4 D.5
4、定义:在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径,点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即或或等,则点P关于极轴对称的点Q的极坐标表示不正确的是( )
A. B. C. D.
5、如图,,C为OB上的定点,M,N分别为射线OA、OB上的动点.当的值最小时,的度数为( )
A. B. C. D.
6、如图,在平面直角坐标系中,直线与轴、轴分别相交于点、.,,将沿直线翻折,点的对应点恰好落双曲线(是常数,)的图像上,则的值为( )
A. B. C. D.
7、如图,在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点A坐标是,则经过第2021次变换后点A的对应点的坐标为( )
A. B. C. D.
8、如图,将三角形纸片ABC沿DE折叠,使B与C重合,CD,AE相交于F,已知BD=4AD,设△ABC的面积为S,△CEF的面积为S1,△ADF的面积为S2,则的值为( )
A. B. C. D.
二、填空题
1、已知点,若点M关于x轴的对称点在第三象限,则a的取值范围是______.
2、如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、,若CD//BE,,则的度数是________.
3、仔细观察图1,体会图1的几何意义.用图1的方法和结论操作一长方形纸片得图2或图3或······,OC,OD均是折痕,当B'在∠COA'的内部时,连接OB',若∠AOC=44°,∠BOD=61°,∠A'OB'的度数是___________.
4、如图,在平面直角坐标系中,点A的坐标是,点B的坐标是,在y轴和x轴上分别有两点P、Q,则A,B,P,Q四点组成的四边形的最小周长为__.
5、如图,是内一定点,点,分别在边,上运动,若,,则的周长的最小值为___________.
6、在平面直角坐标系中,点与点关于x轴对称,则的值是______.
三、解答题
1、作图计算题.如图,在正方形网格上有一个(三个顶点均在格点上,网格上的最小正方形的边长为1).
(1)作关于直线的轴对称图形(不写作法);
(2)画出中边上的高;
(3)画一个锐角(要求各顶点在格点上),使其面积等于的面积.
(4)在HG上画出点,使最小.
2、如图,三个顶点的坐标分别是,,.
(1)试画出关于轴对称的,并写出、、的坐标;
(2)在轴上求作一点,使周长最小,试画出,直接写出点的坐标.
3、如图,在三角形纸片ABC中,AB=12,BC=7,AC=9,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,求△AED的周长.
4、在平面直角坐标系中,的三个顶点的位置如图所示.
(1)请画出关于轴对称的;
(2)直接写出关于轴对称的的,,三点的坐标:__________,__________,__________;
(3)求的面积.
5、如图,是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,,,在边上取一点D,将纸片沿翻折,使点O落在边上的点E处.
(1)求的长;
(2)求D,E两点的坐标.
6、如图,长方形,点E是上的一点,将沿折叠后得到,且点O在长方形内部.已知,.
(1)如图1,若,求四边形的面积.
(2)如图2,延长交于F,连结,将沿折叠,当点D的对称点恰好为点O时,求四边形的面积.
(3)如图3,在(2)的条件下,延长交于点G,连结,将沿折叠,当点C的对称点恰好为点O时,求四边形的面积.
