2.1.1两条直线的位置关系（1）课件

(共27张PPT)
第二章 相交线与平行线
2.1 两条直线的位置关系
第1课时 相交线
生活中处处可见建筑物、道路、桥梁、山川等。在大自然的杰作和人类的创造物中，蕴含着无数的相交线和平行线。
情景引入
观察下面几幅图片，思考：在同一平面内，两条直线的位置关系有几种？
公路
铁路
天桥
在同一平面内，两条直线的位置关系有______和______两种.
探究新知
探究一：相交线平行线
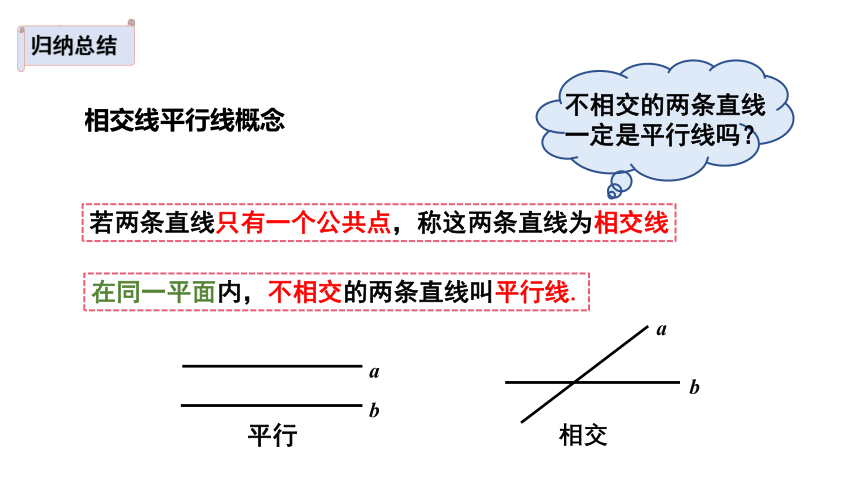
若两条直线只有一个公共点，称这两条直线为相交线
相交
a
b
在同一平面内，不相交的两条直线叫平行线.
a
b
平行
不相交的两条直线一定是平行线吗？
相交线平行线概念
归纳总结
同一平面内两直线的位置关系：
平行
相交
a
b
b
a
在同一平面内，不重合的两直线的位置关系只有平行与相交两种.
注意：平行线的定义包含三层意思：
（1）“在同一平面内”是前提条件；
（2）“不相交”就是说两条直线没有交点；
（3）平行线指的是“两条直线”而不是两条射线或两条线段．
练一练：下列说法中，正确的个数有（　　 ）
（1）在同一平面内不相交的两条线段必平行
（2）在同一平面内不相交的两条直线必平行
（3）在同一平面内不平行的两条线段必相交
（4）在同一平面内不平行的两条直线必相交
A．1个 B．2个 C．3个 D．4个
B
√
×
×
√
针对训练
如图，把两根木条用钉子钉在一起，转动其中一根木条，观察两根木条所形成的角的位置及大小关系.
你能动手画出两条相交直线吗
探究二：对顶角的概念及性质
探究新知
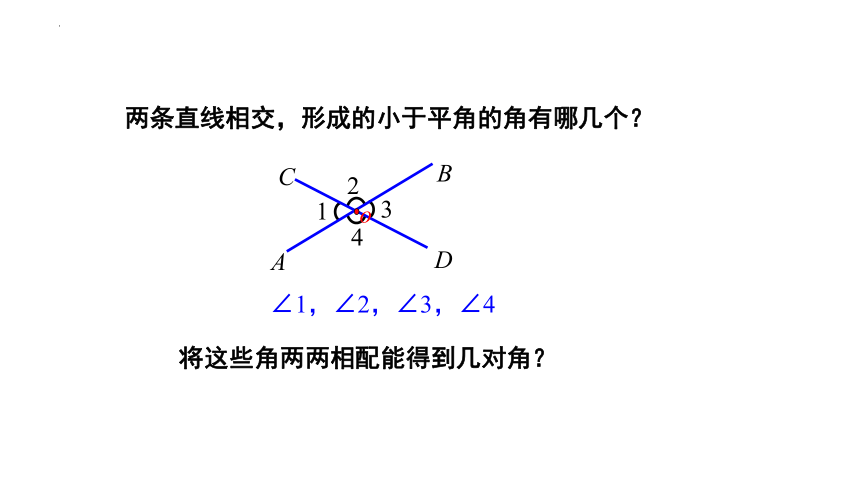
∠1，∠2，∠3，∠4
两条直线相交，形成的小于平角的角有哪几个？
1
2
3
4
B
A
C
D
o
将这些角两两相配能得到几对角？
分类
两直线相交
∠1 和∠3
位置关系
你能根据这几对角的位置关系，对它们进行分类吗？
B
A
C
D
2
4
1
3
∠2 和∠4
1.有公共顶点
3.两边互为反向延长线
2.没有公共边
图中的对顶角有:_________、_________.
A
B
C
D
O
1
3
4
2
∠1与∠3
∠2与∠4
如图，直线AB与CD相交于点O，∠1与∠3有____________，它们的两边________________，具有这种位置关系的两个角叫做________.
公共顶点O
对顶角
互为反向延长线
归纳总结
特别关注：（1）对顶角只有在两条直线相交时才出现．
（2）对顶角是指两个角的位置关系．
练一练：下列各组角中，∠1与∠2是对顶角的为 ( )
D
针对训练
C
O
A
B
D
4
3
2
1
探究：∠1 与∠3在数量上又有什么关系呢？
讨论：你能利用有关知识来验证∠1与∠3的数量关系吗？
猜想：对顶角相等
O
A
B
C
D
4
3
2
1
已知：直线AB与CD相交于O点(如图),
求证:∠1=∠3， ∠2=∠4.
证明：因为直线AB与CD相交于O点,
所以∠1+∠2=180°
∠2+∠3=180°，
所以∠1=∠3.
同理可得∠2=∠4.
符号语言：因为直线AB与CD相交于O点，
所以∠1=∠3，∠2=∠4.
1
2
如果两个角的和是90°，那么称这两个角互为余角.
注：两个角不一定有公共边.
探究三：补角和余角的概念
探究新知
用手中的三角板，画一个直角三角形，如图1.
C
A
B
则∠A+∠B=_____.
图1
90
如果两个角的和是90°，那么称这两个角互为_______.
余角
3
4
如果两个角的和是180°，那么称这两个角互为补角.
注：两个角不一定有公共边.
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x°(x<90)
90° x°
180° x°
观察可得结论：
同一个锐角的补角比它的余角大________.
90°
针对训练
如图，已知：直线AB与CD交于点O， ∠EOD=90°.
回答下列问题：
（1）∠AOE的余角是_______________，补角是______；
（2）∠AOC的余角是______，补角是______， 对顶角是_______.
C
A
B
D
O
E
针对训练
图1
N
2
D
C
O
1
3
4
A
B
图2
打台球时，选择适当的方向，用白球击打红球，反弹后的红球会直接入袋，此时∠1=∠2，将图1抽象成图2，ON与DC交于点O，∠DON=∠CON=900，∠1=∠2.
探究四：补角和余角性质
探究新知
观察思考，在图2中，解决下列问题：
1.哪些角互为补角？哪些角互为余角？
2.∠3与∠4有什么关系？为什么？
3.∠AOC与∠BOD有什么关系？为什么？
N
图2
解：
(1)∠1与∠ AOC, ∠2与∠ BOD互补;
∠1与∠ 3, ∠2与∠ 4互余；
2
D
C
O
1
3
4
A
B
（2）因为∠1= ∠2，
∠ 1+∠3=90° ,
∠ 2+∠4=90°，
所以 ∠ 3=∠4.
同角(等角)的余角相等
归纳总结：同角(等角)的补角相等，同角(等角)的余角相等.
N
2
D
C
O
1
3
4
A
B
图2
（3）因为∠1= ∠2，
∠1+∠AOC=180°,
∠ 2+∠BOD=180°，
所以∠AOC=∠BOD.
同角(等角)的补角相等
互余 互补
两角间的数量关系
对应图形
性质
同角或等角的
余角相等
同角或等角的
补角相等
互余与
互补只与
角的数值
有关，与位
置无关。
而对顶角是
根据角的
位置来
判断的
归纳总结
课堂总结
两直线的位置关系
平行
在同一平面内，不相交的两条直线叫做平行线.
相交
在同一平面内，若两条直线只有一个公共点，我们称这两条直线为相交线.
对顶角
补角
余角
有公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，这样的两个角，互为对顶角．
对顶角相等.
如果两个角的和是90°，那么称这两个角互为余角.
同角或等角的余角相等
如果两个角的和是180°，
那么称这两个角互为补角.
同角或等角的补角相等
课堂小结
课堂练习
1．如图，下列各组角中，互为对顶角的是（　　）
A．∠1和∠2 B．∠1和∠3
C．∠2和∠4 D．∠2和∠5
A
随堂练习
2.下列说法中，正确的有（　 ）
①对顶角相等
②相等的角是对顶角
③不是对顶角的两个角就不相等
④不相等的角不是对顶角
A．1个 B．2个 C．3个 D．0个
B
√
√
3.如图已知：直线AB与CD交于点O, ∠EOD=900,
回答下列问题：
（1）∠AOE的余角是 ；补角是 ；
（2）∠AOC的余角是 ；补角是 ；
对顶角是 ；
C
A
B
D
O
E
∠AOC
∠BOE
∠AOE
∠BOC
∠BOD
4.如图,∠COD=∠EOD=90°, C、O、E在一条直线上, 且∠2= ∠4, 请说出∠1与∠3之间的关系 并试着说明理由
O
∠1与∠3相等
(等角的余角相等).