北师大版数学七年级下册2.4用尺规作角 课件(共17张PPT)
文档属性
| 名称 | 北师大版数学七年级下册2.4用尺规作角 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 376.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 15:16:33 | ||
图片预览





文档简介
(共17张PPT)
北师大版七年级下册
2.4 尺规作图
第二章 相交线与平行线
1
19
1. 能按照作图语言来完成作图动作,能用尺规作一个角等于已知角,并了解它在尺规作图中的简单应用.
2. 能利用尺规作角的和、差、倍.
素养目标
3. 在尺规作图过程当中,积累数学活动经验,培养动手能力和逻辑分析能力.
在几何里,只用没有刻度的直尺和圆规作图称为尺规作图。
尺规作图中直尺的功能是:
(1)在两点间连接一条线段;
(2)将线段向两方延长。
已知:∠AOB.
求作:作∠A'O'B',使∠A'O'B'=∠AOB.
用尺规作一个角等于已知角
A
B
O
探究新知
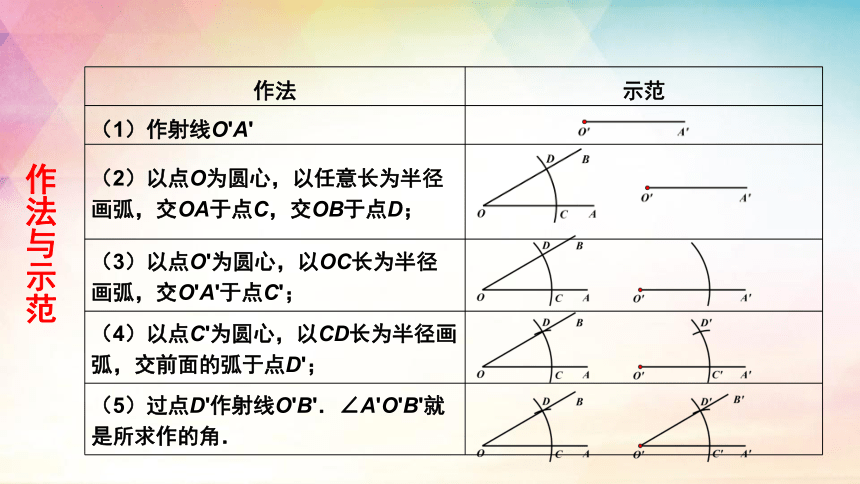
作法 示范
(1)作射线O'A'
(2)以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D;
(3)以点O'为圆心,以OC长为半径画弧,交O'A'于点C';
(4)以点C'为圆心,以CD长为半径画弧,交前面的弧于点D';
(5)过点D'作射线O'B'.∠A'O'B'就是所求作的角.
作法与示范
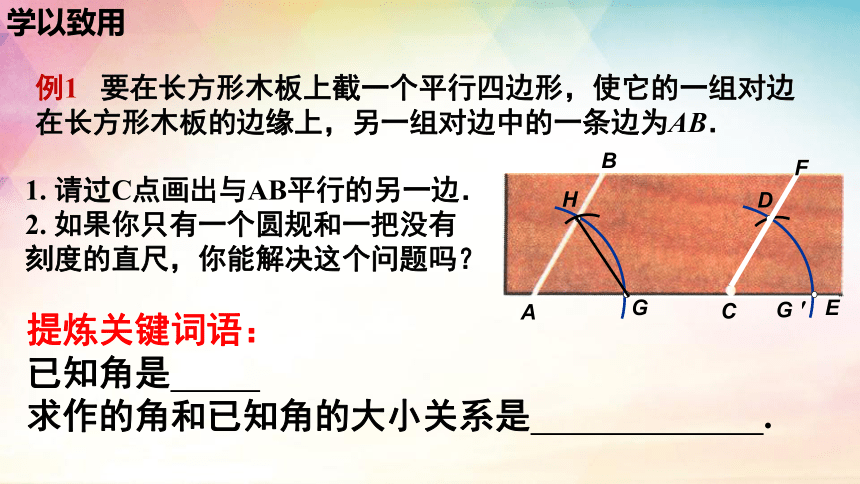
例1 要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB.
1. 请过C点画出与AB平行的另一边.
2. 如果你只有一个圆规和一把没有
刻度的直尺,你能解决这个问题吗?
A
B
C
提炼关键词语:
已知角是
求作的角和已知角的大小关系是 .
A
B
C
E
G
G '
H
D
F
学以致用
B
O
A
独立思考、口述作法、
保留作图痕迹.
作法一:
A’
∠A’OB’即为所求作的角.
B
O
A
作法二:
C
D
C’
E
B’
O’
A’
∠A’O’B’即为所求作的角.
C
B’
典型例题
例2 已知∠AOB,尺规作图作∠A′O′B′,使∠A′O′B′=2∠AOB.
B
O
A
独立思考、口述作法、
保留作图痕迹.
作法一:
A’
∠A’OB’即为所求作的角.
B
O
A
作法二:
C
D
C’
E
B’
O’
A’
∠A’O’B’即为所求作的角.
C
B’
例2 已知∠AOB,尺规作图作∠A′O′B′,使∠A′O′B′=2∠AOB.
1
典型例题
例 3 已知:∠1,∠2,求作∠AOB,使得∠AOB= ∠1+∠2.
2
两角和
1
典型例题
例 4 已知:∠1,∠2,求作∠AOB,使得∠AOB= ∠1-∠2.
2
两角差
例 5 已知如图,锐角∠AOB,求做:∠β,使得∠β =180°-2∠AOB.
分析:首先作出2∠AOB,再求∠AOB的补角即是所求的角.
O
A
B
例 2 已知过直线外一点P作直线 l 的平行线
举一反三
举一反三:还可以怎么画?
1.下列作图属于尺规作图的是( )
A.画线段MN=3cm
B.用量角器画出∠AOB的平分线
C.用三角尺作过点A垂直于直线l的直线
D.已知∠α,用无刻度直尺和圆规作∠AOB,
使∠AOB=2∠α
D
课堂练习
2. 画一个钝角∠AOB,然后以O为顶点,以OA为一边, 在角的内部画一条射线OC,使∠AOC=90°,正确的图形是( )
3.根据图形填空.
(1)连接_____两点.
(2)延长线段____到点___,使BC=____.
(3)在____ AM上截取____=___.
(4)以点O为____ ,以m为____画弧交OA,OB分别
于C,D.
A、B
AB
AB
C
线段
AB
a
圆心
半径
1.尺规作图的基本步骤:
(1)写出已知.(2)写出求作.(3)写出作法并作图.
作图时要保留_________.有时,根据题目要求,可省略作法.
作图痕迹
3.作一个角等于已知角可以归纳为“一线三弧”
先画一条射线,再作三次弧.其中前两次弧半径相同,而第三次以原角的两边与弧的交点之间的距离为半径.
课堂小结
2.基础知识:1.用尺规作一个角等于已知角.
2.用尺规作一个角等于已知角的和、差、倍.
3.借助于已学的用尺规作线段和角来设计图案.
《几何原本》是古希腊数学家欧几里德的一部不朽之作,集整个古希腊数学的成果和精神于一书。它是世界上最著名、最完整而且流传最广的的数学教科书,并且第一次完成了人类对空间的认识。书中系统地总结了古代劳动人民和学者们在实践和思考中获得的几何知识,并把公认的事实列成定义和公理,以形式逻辑
的方法,用这些定义和公理来研究各种几
何图形的性质,从而建立了一套从公理、
定义出发,论证命题得到定理得几何学论
证方法,形成了一个严密的逻辑体系--
几何学。
北师大版七年级下册
2.4 尺规作图
第二章 相交线与平行线
1
19
1. 能按照作图语言来完成作图动作,能用尺规作一个角等于已知角,并了解它在尺规作图中的简单应用.
2. 能利用尺规作角的和、差、倍.
素养目标
3. 在尺规作图过程当中,积累数学活动经验,培养动手能力和逻辑分析能力.
在几何里,只用没有刻度的直尺和圆规作图称为尺规作图。
尺规作图中直尺的功能是:
(1)在两点间连接一条线段;
(2)将线段向两方延长。
已知:∠AOB.
求作:作∠A'O'B',使∠A'O'B'=∠AOB.
用尺规作一个角等于已知角
A
B
O
探究新知
作法 示范
(1)作射线O'A'
(2)以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D;
(3)以点O'为圆心,以OC长为半径画弧,交O'A'于点C';
(4)以点C'为圆心,以CD长为半径画弧,交前面的弧于点D';
(5)过点D'作射线O'B'.∠A'O'B'就是所求作的角.
作法与示范
例1 要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB.
1. 请过C点画出与AB平行的另一边.
2. 如果你只有一个圆规和一把没有
刻度的直尺,你能解决这个问题吗?
A
B
C
提炼关键词语:
已知角是
求作的角和已知角的大小关系是 .
A
B
C
E
G
G '
H
D
F
学以致用
B
O
A
独立思考、口述作法、
保留作图痕迹.
作法一:
A’
∠A’OB’即为所求作的角.
B
O
A
作法二:
C
D
C’
E
B’
O’
A’
∠A’O’B’即为所求作的角.
C
B’
典型例题
例2 已知∠AOB,尺规作图作∠A′O′B′,使∠A′O′B′=2∠AOB.
B
O
A
独立思考、口述作法、
保留作图痕迹.
作法一:
A’
∠A’OB’即为所求作的角.
B
O
A
作法二:
C
D
C’
E
B’
O’
A’
∠A’O’B’即为所求作的角.
C
B’
例2 已知∠AOB,尺规作图作∠A′O′B′,使∠A′O′B′=2∠AOB.
1
典型例题
例 3 已知:∠1,∠2,求作∠AOB,使得∠AOB= ∠1+∠2.
2
两角和
1
典型例题
例 4 已知:∠1,∠2,求作∠AOB,使得∠AOB= ∠1-∠2.
2
两角差
例 5 已知如图,锐角∠AOB,求做:∠β,使得∠β =180°-2∠AOB.
分析:首先作出2∠AOB,再求∠AOB的补角即是所求的角.
O
A
B
例 2 已知过直线外一点P作直线 l 的平行线
举一反三
举一反三:还可以怎么画?
1.下列作图属于尺规作图的是( )
A.画线段MN=3cm
B.用量角器画出∠AOB的平分线
C.用三角尺作过点A垂直于直线l的直线
D.已知∠α,用无刻度直尺和圆规作∠AOB,
使∠AOB=2∠α
D
课堂练习
2. 画一个钝角∠AOB,然后以O为顶点,以OA为一边, 在角的内部画一条射线OC,使∠AOC=90°,正确的图形是( )
3.根据图形填空.
(1)连接_____两点.
(2)延长线段____到点___,使BC=____.
(3)在____ AM上截取____=___.
(4)以点O为____ ,以m为____画弧交OA,OB分别
于C,D.
A、B
AB
AB
C
线段
AB
a
圆心
半径
1.尺规作图的基本步骤:
(1)写出已知.(2)写出求作.(3)写出作法并作图.
作图时要保留_________.有时,根据题目要求,可省略作法.
作图痕迹
3.作一个角等于已知角可以归纳为“一线三弧”
先画一条射线,再作三次弧.其中前两次弧半径相同,而第三次以原角的两边与弧的交点之间的距离为半径.
课堂小结
2.基础知识:1.用尺规作一个角等于已知角.
2.用尺规作一个角等于已知角的和、差、倍.
3.借助于已学的用尺规作线段和角来设计图案.
《几何原本》是古希腊数学家欧几里德的一部不朽之作,集整个古希腊数学的成果和精神于一书。它是世界上最著名、最完整而且流传最广的的数学教科书,并且第一次完成了人类对空间的认识。书中系统地总结了古代劳动人民和学者们在实践和思考中获得的几何知识,并把公认的事实列成定义和公理,以形式逻辑
的方法,用这些定义和公理来研究各种几
何图形的性质,从而建立了一套从公理、
定义出发,论证命题得到定理得几何学论
证方法,形成了一个严密的逻辑体系--
几何学。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
