小升初数学复习课件-行程问题(行车与上下坡问题)人教版(共23张PPT)通用版
文档属性
| 名称 | 小升初数学复习课件-行程问题(行车与上下坡问题)人教版(共23张PPT)通用版 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 20:01:13 | ||
图片预览








文档简介
(共23张PPT)
行程问题:行车问题9
1、两列火车同时从相距1313千米的两地相向开出,3小时后还相距707千米,再经过几小时两车相遇?
速度和=(1313-707)÷3=202(千米/小时)
再经过=707÷202=3.5(小时)
答:再经过3.5小时两车相遇
2、学生甲和乙同时从家里出发相向而行。学生甲每分走52米,学生乙每分走70米,二人在途中A处相遇。若甲提前4分钟出发,且速度不变,学生乙每分改为走90米,则两人仍在A处相遇。问学生甲和乙两人的家相距多少米?
分析:两人仍在A处相遇,如果乙还是以每分钟70走米,那么甲到达A处时,乙距A还有40×7=280米未行,但乙改为每分钟90米,所以,现在乙到A的时间为
280÷(90-70)=14(分钟)
则两地距离为(52+70)×(14+4)=122×18=2196(米)
解设原来X分钟相遇
70X=90(X-4)
x=18
18×(52+70)=2196(米)
答:甲乙两家相距2196米
3、两地之间的路程长300千米,两辆汽车同时从两地相向开出,2.5小时后两车之间还相距50千米,已知一辆汽车每小时行45千米,另一辆汽车每小时行多少千米?
速度和:(300-50)÷2.5=100(千米/小时)
100-45=55(千米/小时)
答:另一辆汽车每小时行55千米。
4、甲、乙两人骑自行车同时从相距97.5千米的两地相向而行,甲的速度是17.5千米/时,乙的速度是15千米/时,几小时后甲、乙两人相距32.5千米?
第一种,两人相差32.5千米相遇
(97.5-32.5)÷(17.5+15)=2(小时)
第二种情况,两人相遇之后相距32.5千米
(97.5+32.5)÷(17.5+15)=4(小时)
5、两条公路成十字交叉,甲从十字路口南1200米处向北直行,乙从十字路口处向东直行。甲、乙同时出发10分钟,两人与十字路口的距离相等,出发后100分钟,两人与十字路口的距离再次相等.此时他们距离十字路口多少米?
解设:甲的速度为x米/分钟,乙的速度为y米/分钟。
则:1200-10X=10y ①
100X-1200=100y ②
整理 120-x=y ①
X-12=y ②
①+② 得108=2y y=54
x=66
54×100=5400米
行程问题:上下坡问题10
1、小明从A到B,先下坡再上坡共用 小时,如果两地相距24千米,下坡每小时行4千米,上坡每小时行3千米,那么原路返回要多少小时?(列方程解应用题)
设小华从A到B上坡路程为x千米,则下坡路程为24-x千米,根据题意可得方程:
4x+72-3x=2×43,
x=14,
24-14=10(千米),
那么可得返回时上坡路为10千米,下坡路为14千米
10/3+14/4=41/6(小时)
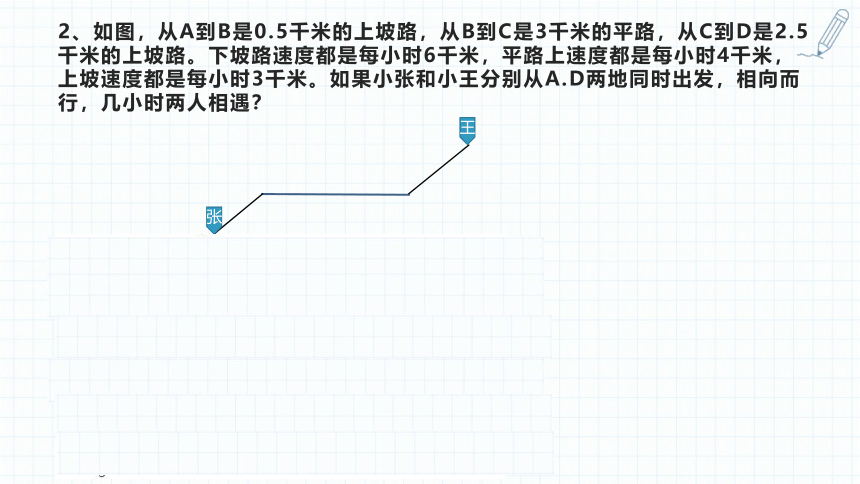
2、如图,从A到B是0.5千米的上坡路,从B到C是3千米的平路,从C到D是2.5千米的上坡路。下坡路速度都是每小时6千米,平路上速度都是每小时4千米,上坡速度都是每小时3千米。如果小张和小王分别从A.D两地同时出发,相向而行,几小时两人相遇?
张
王
3、一段路有上坡、平路、下坡三段,各段路程长的比依次是1:2:3,某人走各段路程所用的时间之比依次是4:5:6,已知他上坡时速度是每小时3千米,路程全长50千米,此人走完全程用多少小时?
4、从甲地到乙地的路有一段平路与一段上坡路,如果骑自行车保持平路每小时行15千米,上坡路每小时行10千米,下坡路每小时行18千米,那么从甲地到乙地需29分钟,从乙地到甲地需25分钟。从甲地到乙地的路程是多少?
解:设平路所用时间为x小时,29分= 29/60小时,25分=25/60小时,
则依据题意得:10( 29/60-x)=18(25/60-x ),
解得:x=1/3 ,
则甲地到乙地的路程是15× +10×(29/60-1/3 )=6.5km,
答:从甲地到乙地的路程是6.5km.
5、甲、乙两人同时从山脚开始爬山,到达山顶后就立即下山,他们两人的下山速度都是各自上山速度的2倍。甲到山顶时,乙距山顶还有400米,甲回到山脚时,乙刚好下到半山腰。求从山顶到山脚的距离?
假设甲乙到达山顶之后继续上行,两人下山速度为上山速度的2倍,
则下山时,甲只能行到山脚到山顶的1/2,同理乙行了1/2÷2=1/4
即甲乙速度比为:(1+1/2):(1+1/4)=6:5
所以,当甲行到山顶时,乙行全程的5/6
400÷(1-5/6)=400÷1/6=2400(米)
答:山顶到山脚2400米
行程问题:变速问题11
1、甲,乙两车分别从A,B两地出发,相向而行。出发时,甲、乙的速度比是5:4,相遇后,甲的速度减小20%,这样当甲到达B地时,乙离A地还有15千米。问:A.B两地相距多少千米?
相遇时,
甲行了全程的5/(5+4)=5/9
乙行了全程的1-5/9=4/9
相遇后,甲速度减少20%
甲乙速度比为5*(1-20%):4=1:1
甲到达B时,又行了全程的4/9
乙又行了全程的4/9
乙与A的距离为全程的1-4/9-4/9=1/9
AB相距:15÷1/9=135千米
2.甲、乙两人分别从A,B两地同时出发,相向而行。出发时他们的速度比是3:2,他们第一次相遇后,甲速度提高了20%,乙速度提高了30%,这样当甲到达B地时,乙离A地还有14千米,那么A,B两地之间的距离是多少千米?
解:第一次相遇时甲乙二人的速度比是3:2
则甲行了全程的3/5,乙行了全程的2/5
相遇后二人的速度比是[3×(1+20%)]:[2×(1+30%)]=18:13
则当甲到达B时,甲乙的行程比是18:13
甲行了2/5,则乙行了(2/5)÷18×13=13/45
此时乙离A地有
1-(13/45)-(2/5)=14/45
全程是
14÷(14/45)=45千米
3.甲,乙两车分别从A,B两地出发,相向而行.出发时,甲,乙的速度比是5:4相遇后,甲的速度减少了20%,乙的速度增加了20%,这样当甲到达B地时,乙离A地还有10千米,那么AB两地相距多少千米
相遇后甲乙速度比=5×(1-20%):4×(1+20%)=5:6
相遇时,乙走了全程的4÷(5+4)=4/9
所以相遇后甲到B地,甲又走了全程的4/9
所以相遇后甲到B地,乙又走了全程4/9÷5×6=8/15
所以乙总共走了全程的4/9+8/15=44/45
所以AB两地的距离=10÷(1-44/45)=10÷1/45=450千米
答:AB两地距离450千米.
4.甲乙两人沿400米环形跑道跑步,俩人同时从跑道的同一地点向相反方向跑去.相遇后甲比原来的速度增加2米/秒,乙比原来的速度减少2米/秒,结果都用24秒同时会到原地.求甲原来的速度!
由题意知,甲增加2米/秒=乙原来的速度;乙速度减少2米/秒=甲原来的速度
所以原来乙的速度比甲快2米/秒
设甲原来的速度为X米/秒,则乙的为X+2米/秒
所以400÷(X+X+2)=24
即200÷(X+1)=24
X+1=200÷24
X=200÷24-1
X=22/3
答:甲原来的速度是22/3米/秒.
行程问题:环形问题12
1、在一个600米的环形跑道上,兄弟两人同时从同一个起点按顺时针方向跑步,两人每隔12分钟相遇一次。若两人速度不变,还是在原来出发点同时出发,哥哥改为按逆时针方向跑,则两人每隔4分钟相遇一次。求跑得快者跑一圈用的时间。
600÷12=50,表示哥哥、弟弟的速度差
600÷4=150,表示哥哥、弟弟的速度和
(50+150)÷2=100,表示较快的速度,方法是求和差问题中的较大数
(150-50)/2=50,表示较慢的速度,方法是求和差问题中的较小数
600÷100=6分钟,表示跑的快者用的时间
2、绕湖环行一周是2700米,甲、乙、丙三人从同一地点出发绕湖行走,甲和乙沿同一方向行走,丙沿反方向行走,甲的速度是每分钟135米,乙的速度是每分钟90米,丙的速度是每分钟45米。当甲与丙相遇后,马上转身反向行走,不久与乙相遇。出发后多长时间,甲与乙相遇?
甲丙相遇时间:2700÷(135+45)=15(分钟),
甲与丙相遇时甲比乙多行:(135-90)×15=675(千米),
甲乙相遇时间:675÷(135+90)=3(分钟),
共用时间:15+3=18(分钟);
答:出发18分钟后,甲与乙相遇.
3、在400米的环形跑道上,小王和小李两人同时并排起跑,小王每秒跑5米,小李每秒跑4.2米,两人起跑后的第一次相遇在起跑线前面多少米。
分析:由于此为一个环形跑道,所以小王第一次追上小李时正好比乙多跑一圈,即400米,根据路程差÷速度差=追及时间可知,小王第一次追上小李需要时间为:400÷(5-4.2)=500秒.则此时小王已经跑了500×5=2500米,即跑了6圈多100米,由此即可解答.
解答: 解:400÷(5-4.2)
=400÷0.8
=500(秒)
500×5÷400
=2500÷400
=6(圈)…100(米)
答:两人起跑后的第一次相遇在起跑线前面100米.
4、甲、乙两人在环形公路上跑步,两人同时从同一地点背向而行,最初甲的速度比乙快1/3,后来乙休息了10分钟,但休息后速度比原来提高了一倍,结果从甲、乙出发开始,经过1小时再次相遇,并且两人跑的路程相同。问乙休息后又跑了多长时间?
路程相同:环形的一半,时间相同:1小时,
解设乙休息后跑了X分钟
1×(60-10-x)+2x=(1+1/3)×60
50-x+2x=80
x=30
5、玲玲、琪琪在某一390米环形道上散步,玲玲从A点逆时针出发,同时琪琪从B点顺时针出发,3分钟后玲玲与琪琪相遇,再过2分钟,玲玲到达B点,又再过4分钟,玲玲与琪琪再次相遇,问玲玲与琪琪每分钟各走多少米?
第一次相遇到第二次相遇实际为2+4=6分钟
速度和为:390÷(2+4)=65(米/秒)
第一次相遇时,A-B路程为:65×3=195(米)
玲玲的速度为195÷(3+2)=39(米/秒)
琪琪的速度为65-39=26(米/秒)
行程问题:行车问题9
1、两列火车同时从相距1313千米的两地相向开出,3小时后还相距707千米,再经过几小时两车相遇?
速度和=(1313-707)÷3=202(千米/小时)
再经过=707÷202=3.5(小时)
答:再经过3.5小时两车相遇
2、学生甲和乙同时从家里出发相向而行。学生甲每分走52米,学生乙每分走70米,二人在途中A处相遇。若甲提前4分钟出发,且速度不变,学生乙每分改为走90米,则两人仍在A处相遇。问学生甲和乙两人的家相距多少米?
分析:两人仍在A处相遇,如果乙还是以每分钟70走米,那么甲到达A处时,乙距A还有40×7=280米未行,但乙改为每分钟90米,所以,现在乙到A的时间为
280÷(90-70)=14(分钟)
则两地距离为(52+70)×(14+4)=122×18=2196(米)
解设原来X分钟相遇
70X=90(X-4)
x=18
18×(52+70)=2196(米)
答:甲乙两家相距2196米
3、两地之间的路程长300千米,两辆汽车同时从两地相向开出,2.5小时后两车之间还相距50千米,已知一辆汽车每小时行45千米,另一辆汽车每小时行多少千米?
速度和:(300-50)÷2.5=100(千米/小时)
100-45=55(千米/小时)
答:另一辆汽车每小时行55千米。
4、甲、乙两人骑自行车同时从相距97.5千米的两地相向而行,甲的速度是17.5千米/时,乙的速度是15千米/时,几小时后甲、乙两人相距32.5千米?
第一种,两人相差32.5千米相遇
(97.5-32.5)÷(17.5+15)=2(小时)
第二种情况,两人相遇之后相距32.5千米
(97.5+32.5)÷(17.5+15)=4(小时)
5、两条公路成十字交叉,甲从十字路口南1200米处向北直行,乙从十字路口处向东直行。甲、乙同时出发10分钟,两人与十字路口的距离相等,出发后100分钟,两人与十字路口的距离再次相等.此时他们距离十字路口多少米?
解设:甲的速度为x米/分钟,乙的速度为y米/分钟。
则:1200-10X=10y ①
100X-1200=100y ②
整理 120-x=y ①
X-12=y ②
①+② 得108=2y y=54
x=66
54×100=5400米
行程问题:上下坡问题10
1、小明从A到B,先下坡再上坡共用 小时,如果两地相距24千米,下坡每小时行4千米,上坡每小时行3千米,那么原路返回要多少小时?(列方程解应用题)
设小华从A到B上坡路程为x千米,则下坡路程为24-x千米,根据题意可得方程:
4x+72-3x=2×43,
x=14,
24-14=10(千米),
那么可得返回时上坡路为10千米,下坡路为14千米
10/3+14/4=41/6(小时)
2、如图,从A到B是0.5千米的上坡路,从B到C是3千米的平路,从C到D是2.5千米的上坡路。下坡路速度都是每小时6千米,平路上速度都是每小时4千米,上坡速度都是每小时3千米。如果小张和小王分别从A.D两地同时出发,相向而行,几小时两人相遇?
张
王
3、一段路有上坡、平路、下坡三段,各段路程长的比依次是1:2:3,某人走各段路程所用的时间之比依次是4:5:6,已知他上坡时速度是每小时3千米,路程全长50千米,此人走完全程用多少小时?
4、从甲地到乙地的路有一段平路与一段上坡路,如果骑自行车保持平路每小时行15千米,上坡路每小时行10千米,下坡路每小时行18千米,那么从甲地到乙地需29分钟,从乙地到甲地需25分钟。从甲地到乙地的路程是多少?
解:设平路所用时间为x小时,29分= 29/60小时,25分=25/60小时,
则依据题意得:10( 29/60-x)=18(25/60-x ),
解得:x=1/3 ,
则甲地到乙地的路程是15× +10×(29/60-1/3 )=6.5km,
答:从甲地到乙地的路程是6.5km.
5、甲、乙两人同时从山脚开始爬山,到达山顶后就立即下山,他们两人的下山速度都是各自上山速度的2倍。甲到山顶时,乙距山顶还有400米,甲回到山脚时,乙刚好下到半山腰。求从山顶到山脚的距离?
假设甲乙到达山顶之后继续上行,两人下山速度为上山速度的2倍,
则下山时,甲只能行到山脚到山顶的1/2,同理乙行了1/2÷2=1/4
即甲乙速度比为:(1+1/2):(1+1/4)=6:5
所以,当甲行到山顶时,乙行全程的5/6
400÷(1-5/6)=400÷1/6=2400(米)
答:山顶到山脚2400米
行程问题:变速问题11
1、甲,乙两车分别从A,B两地出发,相向而行。出发时,甲、乙的速度比是5:4,相遇后,甲的速度减小20%,这样当甲到达B地时,乙离A地还有15千米。问:A.B两地相距多少千米?
相遇时,
甲行了全程的5/(5+4)=5/9
乙行了全程的1-5/9=4/9
相遇后,甲速度减少20%
甲乙速度比为5*(1-20%):4=1:1
甲到达B时,又行了全程的4/9
乙又行了全程的4/9
乙与A的距离为全程的1-4/9-4/9=1/9
AB相距:15÷1/9=135千米
2.甲、乙两人分别从A,B两地同时出发,相向而行。出发时他们的速度比是3:2,他们第一次相遇后,甲速度提高了20%,乙速度提高了30%,这样当甲到达B地时,乙离A地还有14千米,那么A,B两地之间的距离是多少千米?
解:第一次相遇时甲乙二人的速度比是3:2
则甲行了全程的3/5,乙行了全程的2/5
相遇后二人的速度比是[3×(1+20%)]:[2×(1+30%)]=18:13
则当甲到达B时,甲乙的行程比是18:13
甲行了2/5,则乙行了(2/5)÷18×13=13/45
此时乙离A地有
1-(13/45)-(2/5)=14/45
全程是
14÷(14/45)=45千米
3.甲,乙两车分别从A,B两地出发,相向而行.出发时,甲,乙的速度比是5:4相遇后,甲的速度减少了20%,乙的速度增加了20%,这样当甲到达B地时,乙离A地还有10千米,那么AB两地相距多少千米
相遇后甲乙速度比=5×(1-20%):4×(1+20%)=5:6
相遇时,乙走了全程的4÷(5+4)=4/9
所以相遇后甲到B地,甲又走了全程的4/9
所以相遇后甲到B地,乙又走了全程4/9÷5×6=8/15
所以乙总共走了全程的4/9+8/15=44/45
所以AB两地的距离=10÷(1-44/45)=10÷1/45=450千米
答:AB两地距离450千米.
4.甲乙两人沿400米环形跑道跑步,俩人同时从跑道的同一地点向相反方向跑去.相遇后甲比原来的速度增加2米/秒,乙比原来的速度减少2米/秒,结果都用24秒同时会到原地.求甲原来的速度!
由题意知,甲增加2米/秒=乙原来的速度;乙速度减少2米/秒=甲原来的速度
所以原来乙的速度比甲快2米/秒
设甲原来的速度为X米/秒,则乙的为X+2米/秒
所以400÷(X+X+2)=24
即200÷(X+1)=24
X+1=200÷24
X=200÷24-1
X=22/3
答:甲原来的速度是22/3米/秒.
行程问题:环形问题12
1、在一个600米的环形跑道上,兄弟两人同时从同一个起点按顺时针方向跑步,两人每隔12分钟相遇一次。若两人速度不变,还是在原来出发点同时出发,哥哥改为按逆时针方向跑,则两人每隔4分钟相遇一次。求跑得快者跑一圈用的时间。
600÷12=50,表示哥哥、弟弟的速度差
600÷4=150,表示哥哥、弟弟的速度和
(50+150)÷2=100,表示较快的速度,方法是求和差问题中的较大数
(150-50)/2=50,表示较慢的速度,方法是求和差问题中的较小数
600÷100=6分钟,表示跑的快者用的时间
2、绕湖环行一周是2700米,甲、乙、丙三人从同一地点出发绕湖行走,甲和乙沿同一方向行走,丙沿反方向行走,甲的速度是每分钟135米,乙的速度是每分钟90米,丙的速度是每分钟45米。当甲与丙相遇后,马上转身反向行走,不久与乙相遇。出发后多长时间,甲与乙相遇?
甲丙相遇时间:2700÷(135+45)=15(分钟),
甲与丙相遇时甲比乙多行:(135-90)×15=675(千米),
甲乙相遇时间:675÷(135+90)=3(分钟),
共用时间:15+3=18(分钟);
答:出发18分钟后,甲与乙相遇.
3、在400米的环形跑道上,小王和小李两人同时并排起跑,小王每秒跑5米,小李每秒跑4.2米,两人起跑后的第一次相遇在起跑线前面多少米。
分析:由于此为一个环形跑道,所以小王第一次追上小李时正好比乙多跑一圈,即400米,根据路程差÷速度差=追及时间可知,小王第一次追上小李需要时间为:400÷(5-4.2)=500秒.则此时小王已经跑了500×5=2500米,即跑了6圈多100米,由此即可解答.
解答: 解:400÷(5-4.2)
=400÷0.8
=500(秒)
500×5÷400
=2500÷400
=6(圈)…100(米)
答:两人起跑后的第一次相遇在起跑线前面100米.
4、甲、乙两人在环形公路上跑步,两人同时从同一地点背向而行,最初甲的速度比乙快1/3,后来乙休息了10分钟,但休息后速度比原来提高了一倍,结果从甲、乙出发开始,经过1小时再次相遇,并且两人跑的路程相同。问乙休息后又跑了多长时间?
路程相同:环形的一半,时间相同:1小时,
解设乙休息后跑了X分钟
1×(60-10-x)+2x=(1+1/3)×60
50-x+2x=80
x=30
5、玲玲、琪琪在某一390米环形道上散步,玲玲从A点逆时针出发,同时琪琪从B点顺时针出发,3分钟后玲玲与琪琪相遇,再过2分钟,玲玲到达B点,又再过4分钟,玲玲与琪琪再次相遇,问玲玲与琪琪每分钟各走多少米?
第一次相遇到第二次相遇实际为2+4=6分钟
速度和为:390÷(2+4)=65(米/秒)
第一次相遇时,A-B路程为:65×3=195(米)
玲玲的速度为195÷(3+2)=39(米/秒)
琪琪的速度为65-39=26(米/秒)
同课章节目录
