【解析版】江苏省南京市盐城市2014届高三二模数学(理)试题
文档属性
| 名称 | 【解析版】江苏省南京市盐城市2014届高三二模数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 718.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-19 10:08:18 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
( http: / / www.21cnjy.com )
一、填空题
1.【题文】函数f(x)=lnx+的定义域为 .
( http: / / www.21cnjy.com )【结束】
2.【题文】已知复数z1=-2+i,z2=a+2i(i为虚数单位,aR).若z1z2为实数,则a的值为 .[]
( http: / / www.21cnjy.com )【结束】
3.【题文】某地区教育主管部门为了对该地 ( http: / / www.21cnjy.com )区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有 .21cnjy.com
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
【解析】
( http: / / www.21cnjy.com )【结束】
4.【题文】盒中有3张分别标有1,2, 3 ( http: / / www.21cnjy.com )的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为 . 【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )【结束】
5.【题文】已知等差数列{an}的公差d不为0,且a1,a3,a7成等比数列,则的值为 .
( http: / / www.21cnjy.com )【结束】
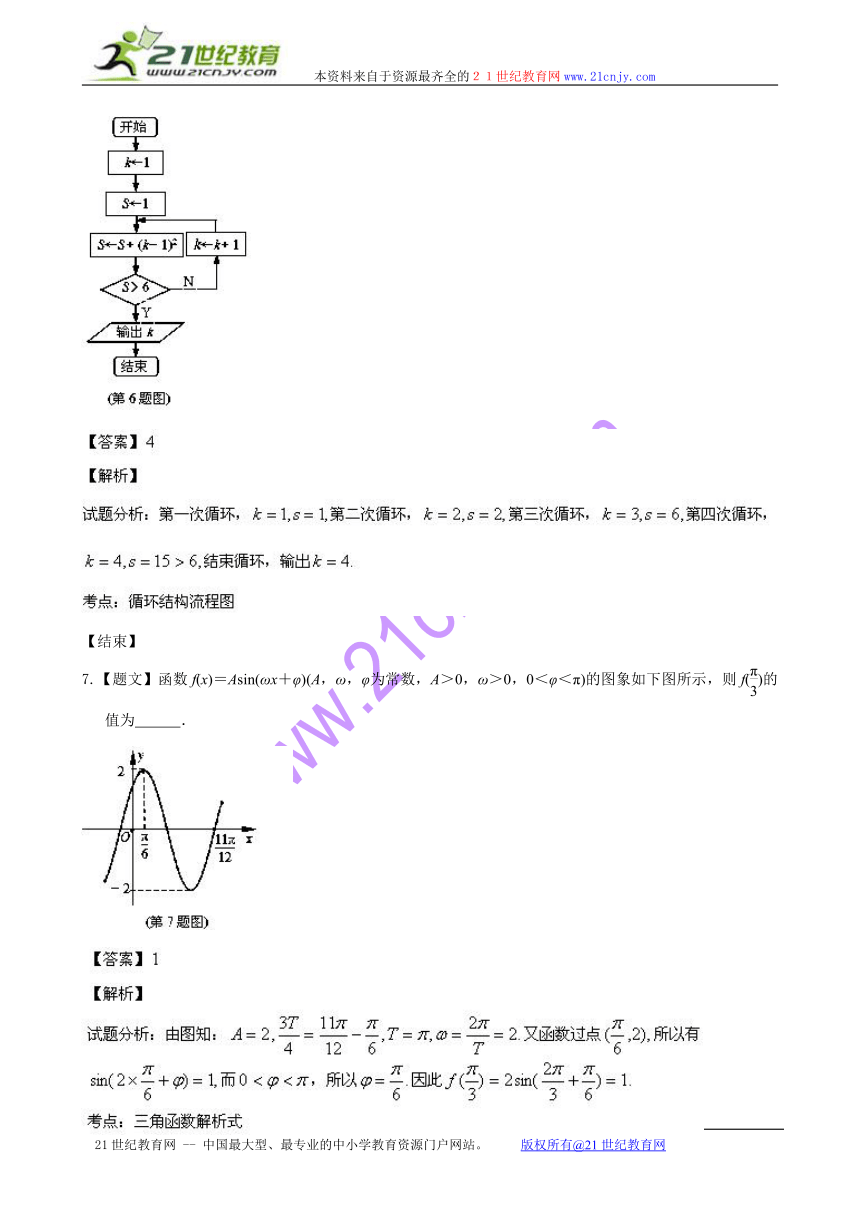
6.【题文】执行如图所示的流程图,则输出的k的值为 .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )【结束】
7.【题文】函数f(x)=Asin(ωx+ ( http: / / www.21cnjy.com )φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如下图所示,则f()的值为 . 21·世纪*教育网
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
【结束】
8.【题文】在平面直角坐标 ( http: / / www.21cnjy.com )系xOy中,双曲线-=1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线相交于A,B两点.若△AOB的面积为2,则双曲线的离心率为 .www-2-1-cnjy-com
( http: / / www.21cnjy.com )
【结束】
9.【题文】表面积为12π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为 .
( http: / / www.21cnjy.com )【结束】
10.【题文】已知||=1,||=2,∠AOB=,=+,则与的夹角大小为 .www.21-cn-jy.com
( http: / / www.21cnjy.com )
【结束】
11.【题文】在平面直角坐标系xOy中 ( http: / / www.21cnjy.com ),过点P(5,3)作直线l与圆x2+y2=4相交于A,B两点,若OA⊥OB,则直线l的斜率为 .2-1-c-n-j-y
( http: / / www.21cnjy.com )
【结束】
12.【题文】已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),且. 21*cnjy*com
若直线y=kx与函数y=f(x)的图象恰有5个不同的公共点,则实数k的值为 .
( http: / / www.21cnjy.com )考点:分段函数图像
【结束】
13.【题文】在△ABC中,点D在边BC上,且DC=2BD,AB∶AD∶AC=3∶k∶1,则实数k的取值范围为 .21教育名师原创作品
( http: / / www.21cnjy.com )
【结束】
14.【题文】设函数f(x)=ax ( http: / / www.21cnjy.com )+sinx+cosx.若函数f(x)的图象上存在不同的两点A,B,使得曲线y=f(x)在点A,B处的切线互相垂直,则实数a的取值范围为 .2·1·c·n·j·y
( http: / / www.21cnjy.com )
【结束】
二、解答题
15.【题文】(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB, BP=BC,E为PC的中点.【出处:21教育名师】
(1)求证:AP∥平面BDE;
(2)求证:BE⊥平面PAC.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
【结束】
16.【题文】(本小题满分14分)
在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交
于点A(x1 ,y1 ),α∈(,).将角α终边绕原点按逆时针方向旋转,交单位圆于点B(x2,y2).
(1)若x1=,求x2;
(2)过A,B作x轴的垂线,垂足分别为C,D,记△AOC及 △BOD的面积分别为S1,S2,且S1=S2,求tanα的值.21*cnjy*com
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
【结束】
17.【题文】(本小题满分14分)[]
如图,经过村庄A有两条夹角为60° ( http: / / www.21cnjy.com )的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).【版权所有:21教育】
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
解法五(变换法):
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
答:设计AM=AN=2 km时,工厂产生的噪声对居民的影响最小.…………………………14分
考点:利用正余弦定理解三角形
【结束】
18.【题文】(本小题满分16分)
在平面直角坐标系xOy中,已知椭圆C∶+=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,一条准线方程为x=2.P为椭圆C上一点,直线PF1交椭圆C于另一点Q.【来源:21cnj*y.co*m】
(1)求椭圆C的方程;
(2)若点P的坐标为(0,b),求过P,Q,F2三点的圆的方程; ( http: / / www.21cnjy.com )
(3)若=λ,且λ∈[,2],求 ( http: / / www.21cnjy.com )的最大值.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )解法二:当PQ斜率不存在时,
( http: / / www.21cnjy.com )
【结束】
19.【题文】(本小题满分16分)
已知函数f(x)=ex,a,bR,且a>0.
(1)若a=2,b=1,求函数f(x)的极值;
(2)设g(x)=a(x-1)ex-f(x).
① 当a=1时,对任意x(0,+∞),都有g(x)≥1成立,求b的最大值;
② 设g′(x)为g(x)的导函数.若存在x>1,使g(x)+g′(x)=0成立,求的取值范围.
( http: / / www.21cnjy.com )【解析】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )所以b≤x2-2x-在x∈(0,+∞)上恒成立. …………………………………………8分
记h(x)=x2-2x-(x>0),则h′(x)=.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )设u(x)=(x>1),则u′(x)=eq \F(8x[(x-)2+],(2x-1)2).
因为x>1,u′(x)>0恒成立,所以u(x)在(1,+∞)是增函数,所以u(x)>u(1)=-1,
所以>-1,即的取值范围为(-1,+∞). …………………………………………16分
解法二:因为g (x)=(ax--2a)ex,所以g ′(x)=(+ax--a)ex.
( http: / / www.21cnjy.com )
【结束】
20.【题文】(本小题满分16分)
已知数列{an}的各项都为正数,且对任意n∈N*,a2n-1,a2n,a2n+1成等差数列,
a2n,a2n+1,a2n+2成等比数列.
(1)若a2=1,a5=3,求a1的值;
(2)设a1<a2,求证:对任意n∈N*,且n≥2,都有<.
( http: / / www.21cnjy.com )a2n,a2n+1,a2n+2成等比数列”运用有两个方向,决定本题有两个解题方法.一是等量代换,求出数列通项公式后,比较大小.二是放缩,直接比较大小. 由2a2n=a2n-1+a2n+1,① a=a2na2n+2.②;所以a= ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
又因为-=-==-,
( http: / / www.21cnjy.com )
【结束】
21.【选做题】在A、B、 ( http: / / www.21cnjy.com )C、D四小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.21教育网
21.【题文】A.选修4—1:几何证明选讲
如图,△ABC为圆的内接三角形,AB=AC,BD为圆的弦,且BD∥AC.过点A作圆的切线与
DB的延长线交于点E,AD与BC交于点F.
(1)求证:四边形ACBE为平行四边形;
(2)若AE=6,BD=5,求线段CF的长.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )【结束】
21.【题文】B.选修4—2:矩阵与变换[]
已知矩阵A=的一个特征值为2,其对应的一个特征向量为α=.
(1)求矩阵A;
(2)若A=,求x,y的值.
( http: / / www.21cnjy.com )
【解析】[][]
( http: / / www.21cnjy.com )【结束】
21.【题文】C.选修4—4:坐标系与参数方程
在极坐标系中,求曲线=2cosθ关于直线θ=(R)对称的曲线的极坐标方程.
( http: / / www.21cnjy.com )
【解析】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )【结束】
21.【题文】D.选修4—5:不等式选讲
已知x,yR,且|x+y|≤,|x-y|≤,求证:|x+5y|≤1.
【答案】详见解析
【解析】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )【结束】
22.【题文】(本小题满分10分)
某中学有4位学生申请A,B,C三所大学的自主招生.若每位学生只能申请其中一所大学,且申请其中任何一所大学是等可能的.21·cn·jy·com
(1)求恰有2人申请A大学的概率;
(2)求被申请大学的个数X的概率分布列与数学期望E(X).[]
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )【结束】
23.【题文】(本小题满分10分)
设f(n)是定义在N*上的增函数,f(4)=5,且满足:
①任意n∈N*,f(n)Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).21世纪教育网版权所有
(1)求f(1),f(2),f(3)的值;(2)求f(n)的表达式.
( http: / / www.21cnjy.com )情形.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )因为f(2) f()=f(k+1)+f(+2-1)=f(k+1)+f(),
( http: / / www.21cnjy.com )
【结束】
A
P
M
N
B
C
x
y
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
( http: / / www.21cnjy.com )
一、填空题
1.【题文】函数f(x)=lnx+的定义域为 .
( http: / / www.21cnjy.com )【结束】
2.【题文】已知复数z1=-2+i,z2=a+2i(i为虚数单位,aR).若z1z2为实数,则a的值为 .[]
( http: / / www.21cnjy.com )【结束】
3.【题文】某地区教育主管部门为了对该地 ( http: / / www.21cnjy.com )区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有 .21cnjy.com
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
【解析】
( http: / / www.21cnjy.com )【结束】
4.【题文】盒中有3张分别标有1,2, 3 ( http: / / www.21cnjy.com )的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为 . 【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )【结束】
5.【题文】已知等差数列{an}的公差d不为0,且a1,a3,a7成等比数列,则的值为 .
( http: / / www.21cnjy.com )【结束】
6.【题文】执行如图所示的流程图,则输出的k的值为 .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )【结束】
7.【题文】函数f(x)=Asin(ωx+ ( http: / / www.21cnjy.com )φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如下图所示,则f()的值为 . 21·世纪*教育网
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
【结束】
8.【题文】在平面直角坐标 ( http: / / www.21cnjy.com )系xOy中,双曲线-=1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线相交于A,B两点.若△AOB的面积为2,则双曲线的离心率为 .www-2-1-cnjy-com
( http: / / www.21cnjy.com )
【结束】
9.【题文】表面积为12π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为 .
( http: / / www.21cnjy.com )【结束】
10.【题文】已知||=1,||=2,∠AOB=,=+,则与的夹角大小为 .www.21-cn-jy.com
( http: / / www.21cnjy.com )
【结束】
11.【题文】在平面直角坐标系xOy中 ( http: / / www.21cnjy.com ),过点P(5,3)作直线l与圆x2+y2=4相交于A,B两点,若OA⊥OB,则直线l的斜率为 .2-1-c-n-j-y
( http: / / www.21cnjy.com )
【结束】
12.【题文】已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),且. 21*cnjy*com
若直线y=kx与函数y=f(x)的图象恰有5个不同的公共点,则实数k的值为 .
( http: / / www.21cnjy.com )考点:分段函数图像
【结束】
13.【题文】在△ABC中,点D在边BC上,且DC=2BD,AB∶AD∶AC=3∶k∶1,则实数k的取值范围为 .21教育名师原创作品
( http: / / www.21cnjy.com )
【结束】
14.【题文】设函数f(x)=ax ( http: / / www.21cnjy.com )+sinx+cosx.若函数f(x)的图象上存在不同的两点A,B,使得曲线y=f(x)在点A,B处的切线互相垂直,则实数a的取值范围为 .2·1·c·n·j·y
( http: / / www.21cnjy.com )
【结束】
二、解答题
15.【题文】(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB, BP=BC,E为PC的中点.【出处:21教育名师】
(1)求证:AP∥平面BDE;
(2)求证:BE⊥平面PAC.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
【结束】
16.【题文】(本小题满分14分)
在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交
于点A(x1 ,y1 ),α∈(,).将角α终边绕原点按逆时针方向旋转,交单位圆于点B(x2,y2).
(1)若x1=,求x2;
(2)过A,B作x轴的垂线,垂足分别为C,D,记△AOC及 △BOD的面积分别为S1,S2,且S1=S2,求tanα的值.21*cnjy*com
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
【结束】
17.【题文】(本小题满分14分)[]
如图,经过村庄A有两条夹角为60° ( http: / / www.21cnjy.com )的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).【版权所有:21教育】
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
解法五(变换法):
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
答:设计AM=AN=2 km时,工厂产生的噪声对居民的影响最小.…………………………14分
考点:利用正余弦定理解三角形
【结束】
18.【题文】(本小题满分16分)
在平面直角坐标系xOy中,已知椭圆C∶+=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,一条准线方程为x=2.P为椭圆C上一点,直线PF1交椭圆C于另一点Q.【来源:21cnj*y.co*m】
(1)求椭圆C的方程;
(2)若点P的坐标为(0,b),求过P,Q,F2三点的圆的方程; ( http: / / www.21cnjy.com )
(3)若=λ,且λ∈[,2],求 ( http: / / www.21cnjy.com )的最大值.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )解法二:当PQ斜率不存在时,
( http: / / www.21cnjy.com )
【结束】
19.【题文】(本小题满分16分)
已知函数f(x)=ex,a,bR,且a>0.
(1)若a=2,b=1,求函数f(x)的极值;
(2)设g(x)=a(x-1)ex-f(x).
① 当a=1时,对任意x(0,+∞),都有g(x)≥1成立,求b的最大值;
② 设g′(x)为g(x)的导函数.若存在x>1,使g(x)+g′(x)=0成立,求的取值范围.
( http: / / www.21cnjy.com )【解析】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )所以b≤x2-2x-在x∈(0,+∞)上恒成立. …………………………………………8分
记h(x)=x2-2x-(x>0),则h′(x)=.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )设u(x)=(x>1),则u′(x)=eq \F(8x[(x-)2+],(2x-1)2).
因为x>1,u′(x)>0恒成立,所以u(x)在(1,+∞)是增函数,所以u(x)>u(1)=-1,
所以>-1,即的取值范围为(-1,+∞). …………………………………………16分
解法二:因为g (x)=(ax--2a)ex,所以g ′(x)=(+ax--a)ex.
( http: / / www.21cnjy.com )
【结束】
20.【题文】(本小题满分16分)
已知数列{an}的各项都为正数,且对任意n∈N*,a2n-1,a2n,a2n+1成等差数列,
a2n,a2n+1,a2n+2成等比数列.
(1)若a2=1,a5=3,求a1的值;
(2)设a1<a2,求证:对任意n∈N*,且n≥2,都有<.
( http: / / www.21cnjy.com )a2n,a2n+1,a2n+2成等比数列”运用有两个方向,决定本题有两个解题方法.一是等量代换,求出数列通项公式后,比较大小.二是放缩,直接比较大小. 由2a2n=a2n-1+a2n+1,① a=a2na2n+2.②;所以a= ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
又因为-=-==-,
( http: / / www.21cnjy.com )
【结束】
21.【选做题】在A、B、 ( http: / / www.21cnjy.com )C、D四小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.21教育网
21.【题文】A.选修4—1:几何证明选讲
如图,△ABC为圆的内接三角形,AB=AC,BD为圆的弦,且BD∥AC.过点A作圆的切线与
DB的延长线交于点E,AD与BC交于点F.
(1)求证:四边形ACBE为平行四边形;
(2)若AE=6,BD=5,求线段CF的长.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )【结束】
21.【题文】B.选修4—2:矩阵与变换[]
已知矩阵A=的一个特征值为2,其对应的一个特征向量为α=.
(1)求矩阵A;
(2)若A=,求x,y的值.
( http: / / www.21cnjy.com )
【解析】[][]
( http: / / www.21cnjy.com )【结束】
21.【题文】C.选修4—4:坐标系与参数方程
在极坐标系中,求曲线=2cosθ关于直线θ=(R)对称的曲线的极坐标方程.
( http: / / www.21cnjy.com )
【解析】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )【结束】
21.【题文】D.选修4—5:不等式选讲
已知x,yR,且|x+y|≤,|x-y|≤,求证:|x+5y|≤1.
【答案】详见解析
【解析】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )【结束】
22.【题文】(本小题满分10分)
某中学有4位学生申请A,B,C三所大学的自主招生.若每位学生只能申请其中一所大学,且申请其中任何一所大学是等可能的.21·cn·jy·com
(1)求恰有2人申请A大学的概率;
(2)求被申请大学的个数X的概率分布列与数学期望E(X).[]
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )【结束】
23.【题文】(本小题满分10分)
设f(n)是定义在N*上的增函数,f(4)=5,且满足:
①任意n∈N*,f(n)Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).21世纪教育网版权所有
(1)求f(1),f(2),f(3)的值;(2)求f(n)的表达式.
( http: / / www.21cnjy.com )情形.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )因为f(2) f()=f(k+1)+f(+2-1)=f(k+1)+f(),
( http: / / www.21cnjy.com )
【结束】
A
P
M
N
B
C
x
y
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
