【解析版】江苏省苏、锡、常、镇四市2014届高三下学期教学情况调查数学(文)试题
文档属性
| 名称 | 【解析版】江苏省苏、锡、常、镇四市2014届高三下学期教学情况调查数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 456.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-19 10:11:16 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2014年苏、锡、常、镇四市高三教学情况调查(一)
文科数学
一、填空题:
1.已知集合,,若,则 ▲ .
( http: / / www.21cnjy.com )
2.若复数z =(为虚数单位),则 | z | = ▲ .
【答案】
【解析】
试题分析:因为 HYPERLINK "http://www.21cnjy.com" 所以也可利用复数模的性质求解,即
考点:复数的模
3.已知双曲线的离心率为,则实数m的值为 ▲ .
( http: / / www.21cnjy.com )4.一个容量为20的样本数据分组后,分组与频数分别如下: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,2;
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,3; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,4; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,5; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,4; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,2.则样本在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的频率是 ▲ .
【答案】
【解析】
试题分析:因为样本在上的频数共有,所以样本在上的频率是.也可从反面求解,即样本不在上的频数共有,所以样本在上的频率是.21·cn·jy·com
考点:样本频率
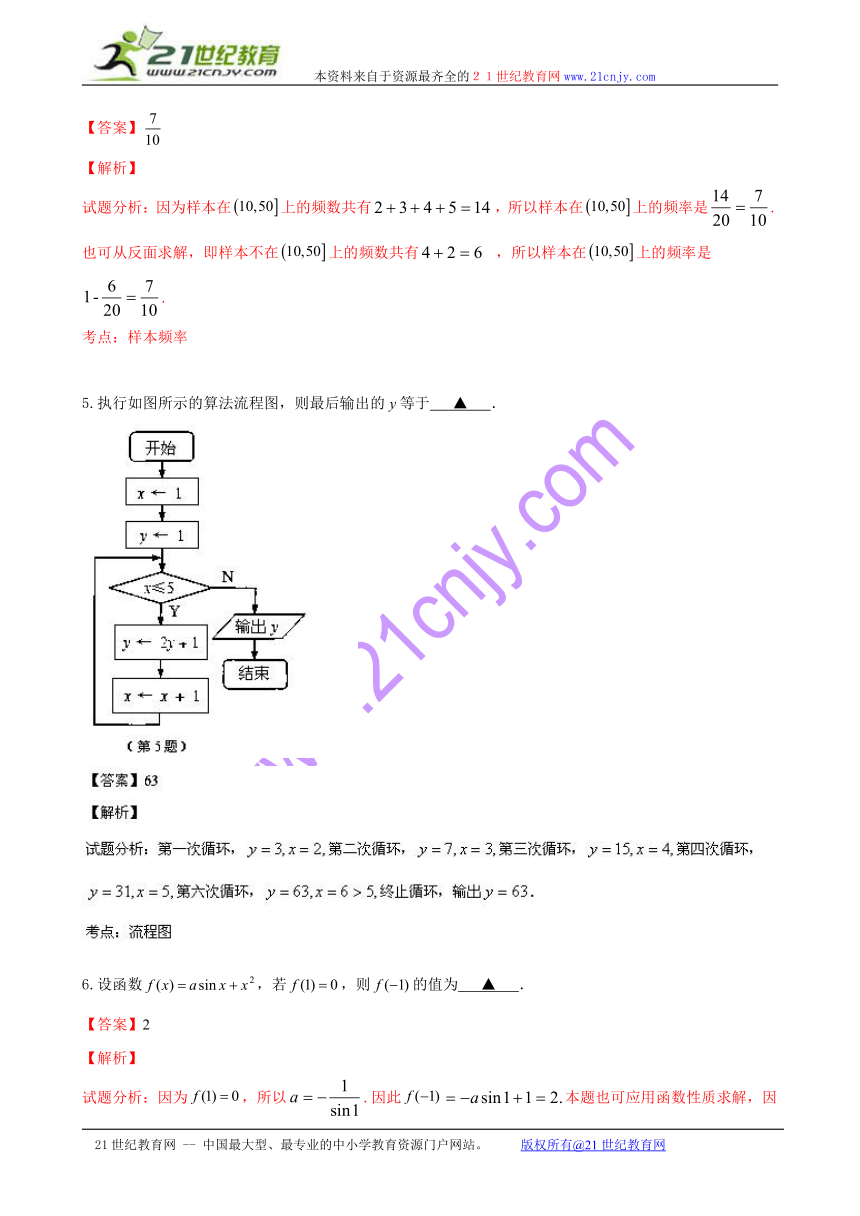
5.执行如图所示的算法流程图,则最后输出的等于 ▲ .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
6.设函数,若,则的值为 ▲ .
【答案】2
【解析】
试题分析:因为,所以.因此 HYPERLINK "http://www.21cnjy.com" 本题也可应用函数性质求解,因为,所以 HYPERLINK "http://www.21cnjy.com"
考点:函数性质
7.四棱锥P ABCD 的底面ABCD是边长为2的正方形,PA⊥底面ABCD
且PA = 4,则PC与底面ABCD所成角的正切值为 ▲ .
( http: / / www.21cnjy.com )
8.从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 ▲ .
( http: / / www.21cnjy.com )9.已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值为 ▲ .
【答案】 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
【解析】
试题分析:因为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
考点:两角和与差正切
10.设等差数列 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的前 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 项和为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则正整数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = ▲ .
( http: / / www.21cnjy.com )11.已知正数满足,则的最小值为 ▲ .
( http: / / www.21cnjy.com )
12.如图,在△ABC中,BO为边AC上的中线,,设∥,若 HYPERLINK "http://www.21cnjy.com" ,则的值为 ▲ .
( http: / / www.21cnjy.com )
【答案】 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
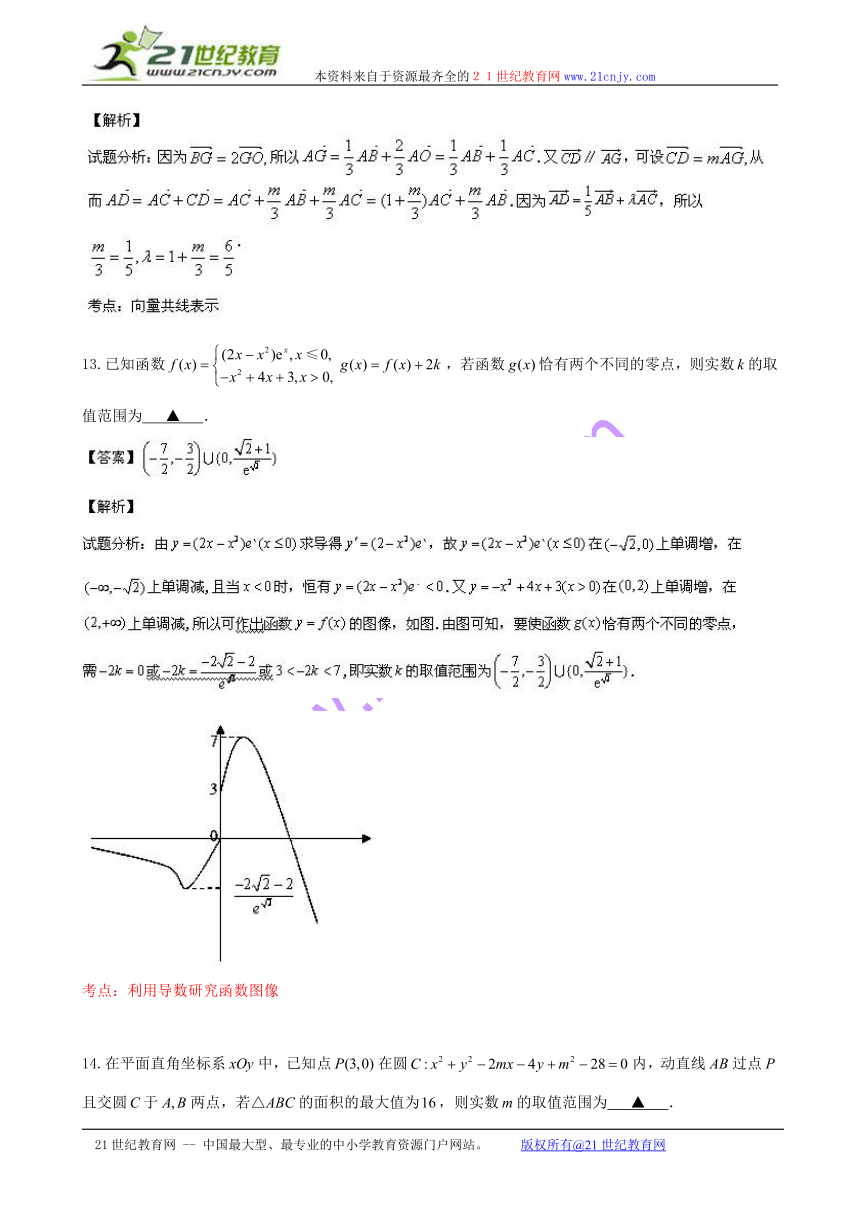
( http: / / www.21cnjy.com )13.已知函数 HYPERLINK "http://www.21cnjy.com" ,若函数恰有两个不同的零点,则实数的取值范围为 ▲ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
考点:利用导数研究函数图像
14.在平面直角坐标系中,已知点在圆内,动直线过点且交圆于两点,若△ABC的面积的最大值为,则实数的取值范围为 ▲ .
( http: / / www.21cnjy.com )
二、解答题
15.(本小题满分14分)
设函数.
(1)求的最小正周期和值域;
(2)在锐角△中,角的对边分别为,若且,,求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 和 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
16.(本小题满分14分)
如图,在三棱柱中,侧面为菱形, 且,,是的中点.
(1)求证:平面平面;
(2)求证:∥平面.
( http: / / www.21cnjy.com )
【答案】(1)详见解析,(2)详见解析.
【解析】
试题分析:(1)证明面面垂直,关键找出线面垂直.因为侧面为菱形, 且,所以△ ( http: / / www.21cnjy.com )
17.(本小题满分14分)
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形(如图所示,其中O为圆心, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在半圆上),设,木梁的体积为V(单位:m3),表面积为S(单位:m2).
(1)求V关于θ的函数表达式;
(2)求的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
( http: / / www.21cnjy.com )
【答案】(1),(2),(3)当木梁的体积V最大时,其表面积S也最大.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
18.(本小题满分16分)
如图,在平面直角坐标系中,已知,,是椭圆上不同的三点,,,在第三象限,线段的中点在直线上.21世纪教育网版权所有
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点在椭圆上(异于点,,)且直线PB,PC分别交直线OA于,两点,证明为定值并求出该定值.21教育网
( http: / / www.21cnjy.com )
【答案】(1)求椭圆方程一般用待定系数法.本题已知椭圆过两点,列两个方程,解出的值,(2)求点的坐标,需列出两个方程.一是点C在椭圆上,即,二是的中点在直线上,即.注意到在第三象限,舍去正值.(3)题意明确,思路简洁,就是求出点的坐标,算出为定值.难点是如何消去参数.因为点在直线: 上,所以可设,.选择作为参数,即用表示点的坐标.由三点共线,解得,同理解得.从而有,这里主要用到代入化简.本题也可利用椭圆参数方程或三角表示揭示为定值.21cnjy.com
( http: / / www.21cnjy.com )∵三点共线,∴,整理,得.…………………10分
∵点在椭圆上,∴,.
从而. …………………14分
所以. …………………15分
∴为定值,定值为. …………………16分
考点:椭圆标准方程,直线与椭圆位置关系
19.(本小题满分16分)
设各项均为正数的数列的前n项和为Sn,已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且对一切都成立.
(1)若λ = 1,求数列的通项公式;
(2)求λ的值,使数列是等差数列.
( http: / / www.21cnjy.com )∴当时,.②
② ①,得, ∴(). ………………… 6分
∵当n = 1时, ,∴n = 1时上式也成立,
∴数列{an}是首项为1,公比为2的等比数列, an = 2n1(). …………………8分
( http: / / www.21cnjy.com )
20.(本小题满分16分)
已知函数,其中m,a均为实数.
(1)求的极值;
(2)设,若对任意的 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,恒成立,求的最小值;
(3)设,若对任意给定的,在区间上总存在,使得 成立,求的取值范围.
【答案】(1)极大值为1,无极小值.(2)3 .(3).
【解析】
( http: / / www.21cnjy.com )试题解析:(1),令,得x = 1. ………………… 1分
列表如下:
x (∞,1) 1 (1,∞)
0
g(x) ↗ 极大值 ↘
∵g(1) = 1,∴y =的极大值为1,无极小值. …………………3分
(2)当时,,.
∵在恒成立,∴在上为增函数. …………………4分
设,∵> 0在恒成立,
∴在上为增函数. …………………5分
设,则等价于,
即.
设,则u(x)在为减函数.
∴在(3,4)上恒成立. …………………6分
∴恒成立.
设,∵=,x[3,4],
∴,∴< 0,为减函数.
∴在 [3,4]上的最大值为v(3) = 3 . ………………… 8分
∴a≥3 ,∴的最小值为3 . …………………9分
( http: / / www.21cnjy.com )∵,∴时,命题成立.
综上所述,的取值范围为. …………………16分
考点:函数极值,不等式恒成立
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2014年苏、锡、常、镇四市高三教学情况调查(一)
文科数学
一、填空题:
1.已知集合,,若,则 ▲ .
( http: / / www.21cnjy.com )
2.若复数z =(为虚数单位),则 | z | = ▲ .
【答案】
【解析】
试题分析:因为 HYPERLINK "http://www.21cnjy.com" 所以也可利用复数模的性质求解,即
考点:复数的模
3.已知双曲线的离心率为,则实数m的值为 ▲ .
( http: / / www.21cnjy.com )4.一个容量为20的样本数据分组后,分组与频数分别如下: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,2;
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,3; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,4; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,5; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,4; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,2.则样本在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的频率是 ▲ .
【答案】
【解析】
试题分析:因为样本在上的频数共有,所以样本在上的频率是.也可从反面求解,即样本不在上的频数共有,所以样本在上的频率是.21·cn·jy·com
考点:样本频率
5.执行如图所示的算法流程图,则最后输出的等于 ▲ .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
6.设函数,若,则的值为 ▲ .
【答案】2
【解析】
试题分析:因为,所以.因此 HYPERLINK "http://www.21cnjy.com" 本题也可应用函数性质求解,因为,所以 HYPERLINK "http://www.21cnjy.com"
考点:函数性质
7.四棱锥P ABCD 的底面ABCD是边长为2的正方形,PA⊥底面ABCD
且PA = 4,则PC与底面ABCD所成角的正切值为 ▲ .
( http: / / www.21cnjy.com )
8.从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 ▲ .
( http: / / www.21cnjy.com )9.已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值为 ▲ .
【答案】 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
【解析】
试题分析:因为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 .
考点:两角和与差正切
10.设等差数列 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的前 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 项和为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则正整数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = ▲ .
( http: / / www.21cnjy.com )11.已知正数满足,则的最小值为 ▲ .
( http: / / www.21cnjy.com )
12.如图,在△ABC中,BO为边AC上的中线,,设∥,若 HYPERLINK "http://www.21cnjy.com" ,则的值为 ▲ .
( http: / / www.21cnjy.com )
【答案】 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )13.已知函数 HYPERLINK "http://www.21cnjy.com" ,若函数恰有两个不同的零点,则实数的取值范围为 ▲ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
考点:利用导数研究函数图像
14.在平面直角坐标系中,已知点在圆内,动直线过点且交圆于两点,若△ABC的面积的最大值为,则实数的取值范围为 ▲ .
( http: / / www.21cnjy.com )
二、解答题
15.(本小题满分14分)
设函数.
(1)求的最小正周期和值域;
(2)在锐角△中,角的对边分别为,若且,,求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 和 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
16.(本小题满分14分)
如图,在三棱柱中,侧面为菱形, 且,,是的中点.
(1)求证:平面平面;
(2)求证:∥平面.
( http: / / www.21cnjy.com )
【答案】(1)详见解析,(2)详见解析.
【解析】
试题分析:(1)证明面面垂直,关键找出线面垂直.因为侧面为菱形, 且,所以△ ( http: / / www.21cnjy.com )
17.(本小题满分14分)
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形(如图所示,其中O为圆心, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在半圆上),设,木梁的体积为V(单位:m3),表面积为S(单位:m2).
(1)求V关于θ的函数表达式;
(2)求的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
( http: / / www.21cnjy.com )
【答案】(1),(2),(3)当木梁的体积V最大时,其表面积S也最大.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
18.(本小题满分16分)
如图,在平面直角坐标系中,已知,,是椭圆上不同的三点,,,在第三象限,线段的中点在直线上.21世纪教育网版权所有
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点在椭圆上(异于点,,)且直线PB,PC分别交直线OA于,两点,证明为定值并求出该定值.21教育网
( http: / / www.21cnjy.com )
【答案】(1)求椭圆方程一般用待定系数法.本题已知椭圆过两点,列两个方程,解出的值,(2)求点的坐标,需列出两个方程.一是点C在椭圆上,即,二是的中点在直线上,即.注意到在第三象限,舍去正值.(3)题意明确,思路简洁,就是求出点的坐标,算出为定值.难点是如何消去参数.因为点在直线: 上,所以可设,.选择作为参数,即用表示点的坐标.由三点共线,解得,同理解得.从而有,这里主要用到代入化简.本题也可利用椭圆参数方程或三角表示揭示为定值.21cnjy.com
( http: / / www.21cnjy.com )∵三点共线,∴,整理,得.…………………10分
∵点在椭圆上,∴,.
从而. …………………14分
所以. …………………15分
∴为定值,定值为. …………………16分
考点:椭圆标准方程,直线与椭圆位置关系
19.(本小题满分16分)
设各项均为正数的数列的前n项和为Sn,已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且对一切都成立.
(1)若λ = 1,求数列的通项公式;
(2)求λ的值,使数列是等差数列.
( http: / / www.21cnjy.com )∴当时,.②
② ①,得, ∴(). ………………… 6分
∵当n = 1时, ,∴n = 1时上式也成立,
∴数列{an}是首项为1,公比为2的等比数列, an = 2n1(). …………………8分
( http: / / www.21cnjy.com )
20.(本小题满分16分)
已知函数,其中m,a均为实数.
(1)求的极值;
(2)设,若对任意的 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,恒成立,求的最小值;
(3)设,若对任意给定的,在区间上总存在,使得 成立,求的取值范围.
【答案】(1)极大值为1,无极小值.(2)3 .(3).
【解析】
( http: / / www.21cnjy.com )试题解析:(1),令,得x = 1. ………………… 1分
列表如下:
x (∞,1) 1 (1,∞)
0
g(x) ↗ 极大值 ↘
∵g(1) = 1,∴y =的极大值为1,无极小值. …………………3分
(2)当时,,.
∵在恒成立,∴在上为增函数. …………………4分
设,∵> 0在恒成立,
∴在上为增函数. …………………5分
设,则等价于,
即.
设,则u(x)在为减函数.
∴在(3,4)上恒成立. …………………6分
∴恒成立.
设,∵=,x[3,4],
∴,∴< 0,为减函数.
∴在 [3,4]上的最大值为v(3) = 3 . ………………… 8分
∴a≥3 ,∴的最小值为3 . …………………9分
( http: / / www.21cnjy.com )∵,∴时,命题成立.
综上所述,的取值范围为. …………………16分
考点:函数极值,不等式恒成立
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
