【解析版】江苏省苏、锡、常、镇四市2014届高三下学期教学情况调查数学(理)试题
文档属性
| 名称 | 【解析版】江苏省苏、锡、常、镇四市2014届高三下学期教学情况调查数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 618.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-19 10:11:14 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2014年苏、锡、常、镇四市高三教学情况调查(一)
理科数学
一、填空题:
1.已知集合,,若,则 ▲ .
( http: / / www.21cnjy.com )
2.若复数z =(为虚数单位),则 | z | = ▲ .
( http: / / www.21cnjy.com )
3.已知双曲线的离心率为,则实数m的值为 ▲ .
( http: / / www.21cnjy.com )4.一个容量为20的样本数据分组后,分组与频数分别如下: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,2;
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,3; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,4; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,5; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,4; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,2.则样本在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的频率是 ▲ .
( http: / / www.21cnjy.com )
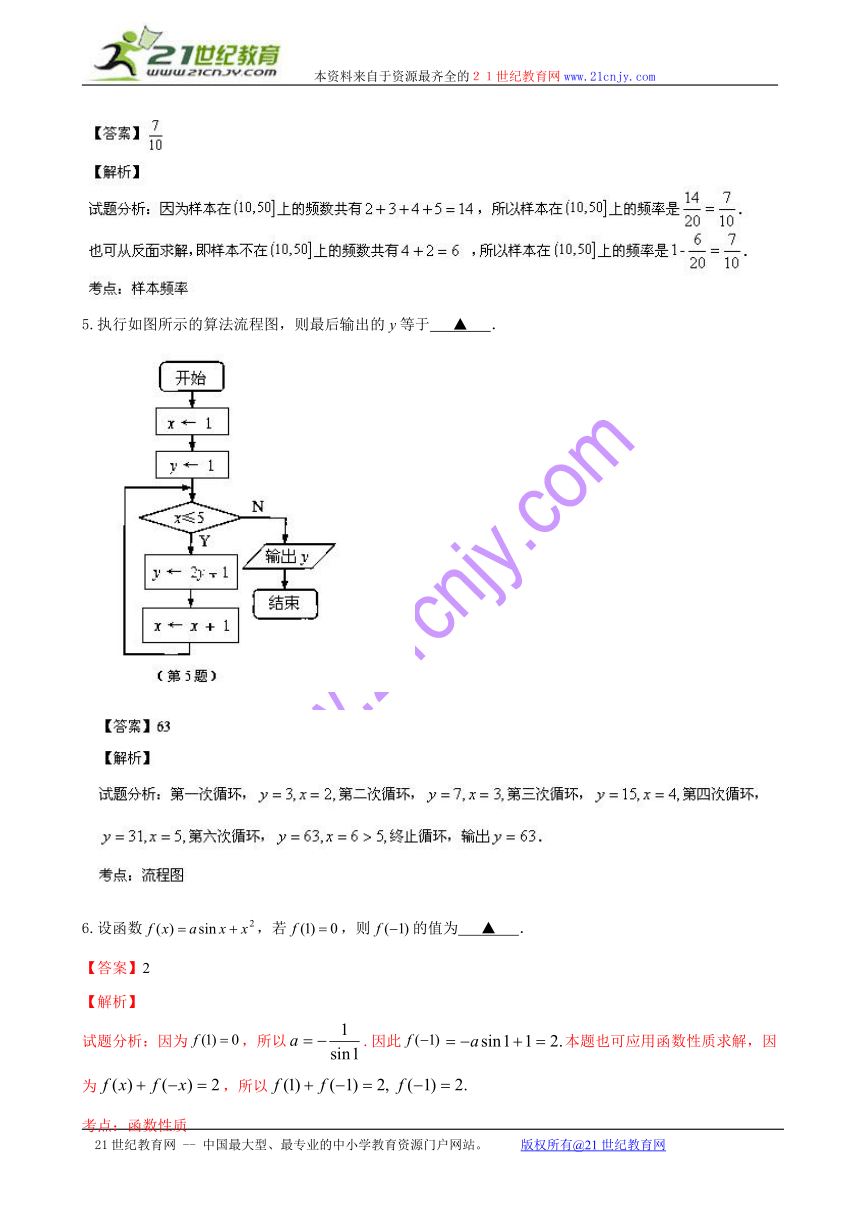
5.执行如图所示的算法流程图,则最后输出的等于 ▲ .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
6.设函数,若,则的值为 ▲ .
【答案】2
【解析】
试题分析:因为,所以.因此 HYPERLINK "http://www.21cnjy.com" 本题也可应用函数性质求解,因为,所以 HYPERLINK "http://www.21cnjy.com"
考点:函数性质
7.四棱锥P ABCD 的底面ABC ( http: / / www.21cnjy.com )D是边长为2的正方形,PA⊥底面ABCD且PA = 4,则PC与底面ABCD所成角的正切值为 ▲ .21世纪教育网版权所有
( http: / / www.21cnjy.com )
8.从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 ▲ .
( http: / / www.21cnjy.com )
9.已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值为 ▲ .
( http: / / www.21cnjy.com )
10.设等差数列 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的前 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 项和为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则正整数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = ▲ .
( http: / / www.21cnjy.com )
11.已知正数满足,则的最小值为 ▲ .
( http: / / www.21cnjy.com )
12.如图,在△ABC中,BO为边AC上的中线,,设∥,若 HYPERLINK "http://www.21cnjy.com" ,则的值为 ▲ .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )考点:向量共线表示
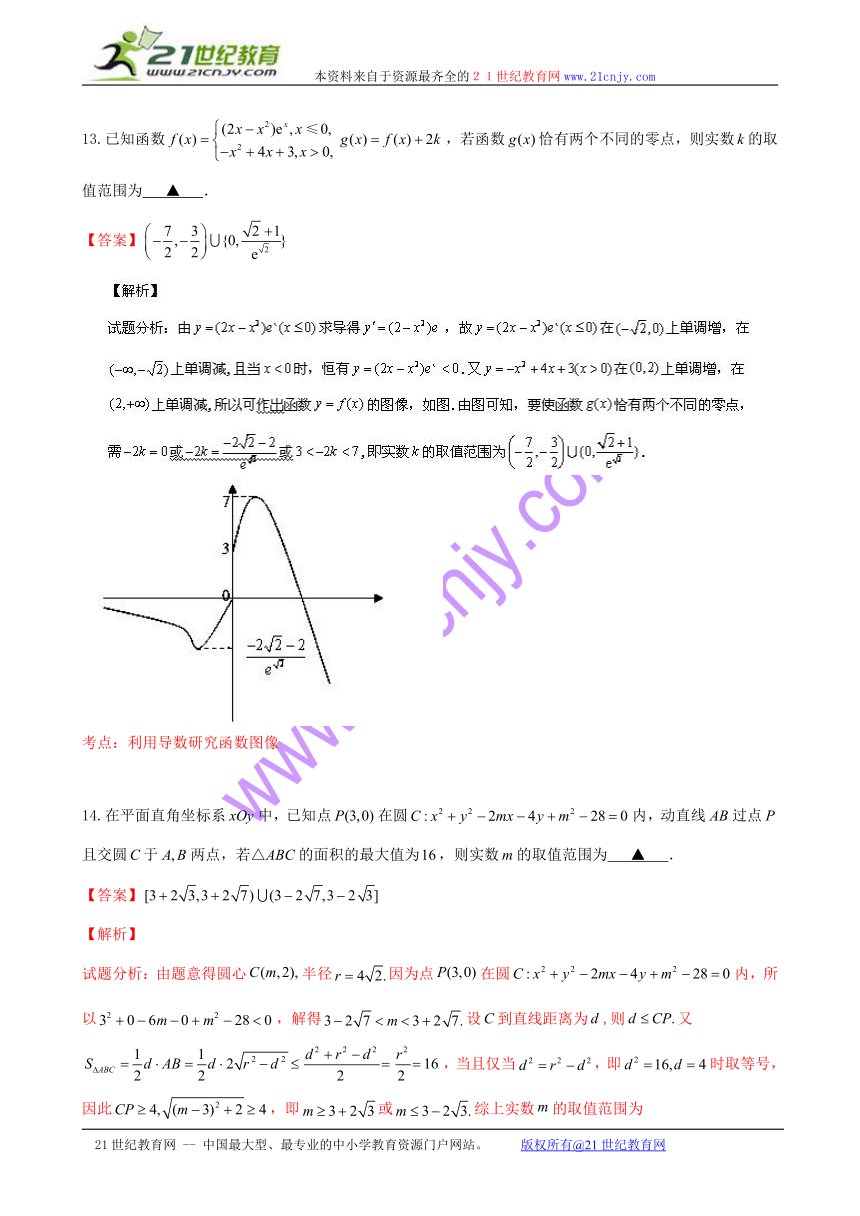
13.已知函数 HYPERLINK "http://www.21cnjy.com" ,若函数恰有两个不同的零点,则实数的取值范围为 ▲ .
【答案】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
考点:利用导数研究函数图像
14.在平面直角坐标系中,已知点在圆内,动直线过点且交圆于两点,若△ABC的面积的最大值为,则实数的取值范围为 ▲ .
【答案】
【解析】
试题分析:由题意得圆心 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 半径 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 因为点在圆内,所以,解得设到直线距离为,则又,当且仅当,即时取等号,因此,即或综上实数的取值范围为.21教育网
考点:直线与圆位置关系
二、解答题
15.(本小题满分14分)
设函数.
(1)求的最小正周期和值域;
(2)在锐角△中,角的对边分别为,若且,,求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 和 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
( http: / / www.21cnjy.com )(2)由,得.
为锐角,∴,,∴. …………………9分
∵,,∴. …………………10分
在△ABC中,由正弦定理得. …………………12分
∴. …………………14分
考点:倍角公式,正余弦定理
16.(本小题满分14分)
如图,在三棱柱中,侧面为菱形, 且,,是的中点.
(1)求证:平面平面;
(2)求证:∥平面.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
17.(本小题满分14分)
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形(如图所示,其中O为圆心, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在半圆上),设,木梁的体积为V(单位:m3),表面积为S(单位:m2).
(1)求V关于θ的函数表达式;
(2)求的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
( http: / / www.21cnjy.com )
【答案】(1),(2),(3)当木梁的体积V最大时,其表面积S也最大.
( http: / / www.21cnjy.com )(3)木梁的侧面积=,.
=,.…………………10分
设,.∵,
∴当,即时,最大. …………………12分
又由(2)知时,取得最大值,
所以时,木梁的表面积S最大. …………………13分
综上,当木梁的体积V最大时,其表面积S也最大. …………………14分
考点:利用导数求函数最值
18.(本小题满分16分)
如图,在平面直角坐标系中,已知,,是椭圆上不同的三点,,,在第三象限,线段的中点在直线上.21cnjy.com
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点在椭圆上(异于点,,)且直线PB,PC分别交直线OA于,两点,证明为定值并求出该定值.21·cn·jy·com
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )可利用椭圆参数方程或三角表示揭示为定值.
【解析】
试题分析:(1),(2),(3).
试题解析:(1)由已知,得 解得 …………………2分
所以椭圆的标准方程为. …………………3分
( http: / / www.21cnjy.com )
19.(本小题满分16分)
设各项均为正数的数列的前n项和为Sn,已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且对一切都成立.
(1)若λ = 1,求数列的通项公式;
(2)求λ的值,使数列是等差数列.
【答案】(1)an = 2n1(2)λ = 0.
【解析】
( http: / / www.21cnjy.com )(2)令n = 1,得.令n = 2,得. ………………… 10分
要使数列是等差数列,必须有,解得λ = 0. ………………… 11分
当λ = 0时,,且.
当n≥2时,,
整理,得,, ………………… 13分
从而,
化简,得,所以. ……………… 15分
综上所述,(),
所以λ = 0时,数列是等差数列. ………………… 16分
考点:已知求
20.(本小题满分16分)
已知函数,其中m,a均为实数.
(1)求的极值;
(2)设,若对任意的 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,恒成立,求的最小值;
(3)设,若对任意给定的,在区间上总存在,使得 成立,求的取值范围.
( http: / / www.21cnjy.com )对于函数在上值域中每一个值,函数在上总有两个不同自变量与之对应相等.首先求出函数在上值域,然后根据函数在上必须不为单调函数且每段单调区间对应的值域都需包含.由在不单调得,由每段单调区间对应的值域都需包含得,.www.21-cn-jy.com
试题解析:(1),令,得x = 1. ………………… 1分
列表如下:
x (∞,1) 1 (1,∞)
0
g(x) ↗ 极大值 ↘
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
附加题
21.【选做题】在A、B、C、D 四小题中 ( http: / / www.21cnjy.com )只能选做两题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.2·1·c·n·j·y
21.A.选修4—1:几何证明选讲
如图,⊙ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为四边形 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的外接圆,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 延长线上一点,直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 相切.
求证: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
( http: / / www.21cnjy.com )
【答案】详见解析
【解析】
( http: / / www.21cnjy.com )
21.B.选修4—2:矩阵与变换
已知矩阵 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,计算 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
【答案】
【解析】
试题分析:利用矩阵特征值及其对应特征向量性质:进行化简.先根据矩阵M的特征多项式求出其特征值,进而求出对应的特征向量,.再将分解成特征向量,即,最后利用性质求结果,即 ( http: / / www.21cnjy.com )
21.C.选修4—4:坐标系与参数方程
在平面直角坐标系 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 中,圆的参数方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,以坐标原点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为极点,轴的正半
轴为极轴建立极坐标系.求:
(1)圆的直角坐标方程;
(2)圆的极坐标方程.
( http: / / www.21cnjy.com )21.D.选修4—5:不等式选讲
已知函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图象恒在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 轴上方,求实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围.
( http: / / www.21cnjy.com )
22.(本小题满分10分)
甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且各次投篮的结果互不影响.甲
同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的分布列和数学期望.
( http: / / www.21cnjy.com )(2)由题意.
,,,,
.
的分布表为
1 2 3 4 5
…………………8分
的数学期望. …………………10分
考点:概率分布,数学期望值
23.(本小题满分10分)
设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,其中当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为偶数时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为奇数时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
(1)证明:当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2014年苏、锡、常、镇四市高三教学情况调查(一)
理科数学
一、填空题:
1.已知集合,,若,则 ▲ .
( http: / / www.21cnjy.com )
2.若复数z =(为虚数单位),则 | z | = ▲ .
( http: / / www.21cnjy.com )
3.已知双曲线的离心率为,则实数m的值为 ▲ .
( http: / / www.21cnjy.com )4.一个容量为20的样本数据分组后,分组与频数分别如下: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,2;
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,3; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,4; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,5; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,4; HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,2.则样本在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的频率是 ▲ .
( http: / / www.21cnjy.com )
5.执行如图所示的算法流程图,则最后输出的等于 ▲ .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
6.设函数,若,则的值为 ▲ .
【答案】2
【解析】
试题分析:因为,所以.因此 HYPERLINK "http://www.21cnjy.com" 本题也可应用函数性质求解,因为,所以 HYPERLINK "http://www.21cnjy.com"
考点:函数性质
7.四棱锥P ABCD 的底面ABC ( http: / / www.21cnjy.com )D是边长为2的正方形,PA⊥底面ABCD且PA = 4,则PC与底面ABCD所成角的正切值为 ▲ .21世纪教育网版权所有
( http: / / www.21cnjy.com )
8.从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 ▲ .
( http: / / www.21cnjy.com )
9.已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值为 ▲ .
( http: / / www.21cnjy.com )
10.设等差数列 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的前 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 项和为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则正整数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = ▲ .
( http: / / www.21cnjy.com )
11.已知正数满足,则的最小值为 ▲ .
( http: / / www.21cnjy.com )
12.如图,在△ABC中,BO为边AC上的中线,,设∥,若 HYPERLINK "http://www.21cnjy.com" ,则的值为 ▲ .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )考点:向量共线表示
13.已知函数 HYPERLINK "http://www.21cnjy.com" ,若函数恰有两个不同的零点,则实数的取值范围为 ▲ .
【答案】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
考点:利用导数研究函数图像
14.在平面直角坐标系中,已知点在圆内,动直线过点且交圆于两点,若△ABC的面积的最大值为,则实数的取值范围为 ▲ .
【答案】
【解析】
试题分析:由题意得圆心 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 半径 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 因为点在圆内,所以,解得设到直线距离为,则又,当且仅当,即时取等号,因此,即或综上实数的取值范围为.21教育网
考点:直线与圆位置关系
二、解答题
15.(本小题满分14分)
设函数.
(1)求的最小正周期和值域;
(2)在锐角△中,角的对边分别为,若且,,求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 和 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
( http: / / www.21cnjy.com )(2)由,得.
为锐角,∴,,∴. …………………9分
∵,,∴. …………………10分
在△ABC中,由正弦定理得. …………………12分
∴. …………………14分
考点:倍角公式,正余弦定理
16.(本小题满分14分)
如图,在三棱柱中,侧面为菱形, 且,,是的中点.
(1)求证:平面平面;
(2)求证:∥平面.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
17.(本小题满分14分)
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形(如图所示,其中O为圆心, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在半圆上),设,木梁的体积为V(单位:m3),表面积为S(单位:m2).
(1)求V关于θ的函数表达式;
(2)求的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
( http: / / www.21cnjy.com )
【答案】(1),(2),(3)当木梁的体积V最大时,其表面积S也最大.
( http: / / www.21cnjy.com )(3)木梁的侧面积=,.
=,.…………………10分
设,.∵,
∴当,即时,最大. …………………12分
又由(2)知时,取得最大值,
所以时,木梁的表面积S最大. …………………13分
综上,当木梁的体积V最大时,其表面积S也最大. …………………14分
考点:利用导数求函数最值
18.(本小题满分16分)
如图,在平面直角坐标系中,已知,,是椭圆上不同的三点,,,在第三象限,线段的中点在直线上.21cnjy.com
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点在椭圆上(异于点,,)且直线PB,PC分别交直线OA于,两点,证明为定值并求出该定值.21·cn·jy·com
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )可利用椭圆参数方程或三角表示揭示为定值.
【解析】
试题分析:(1),(2),(3).
试题解析:(1)由已知,得 解得 …………………2分
所以椭圆的标准方程为. …………………3分
( http: / / www.21cnjy.com )
19.(本小题满分16分)
设各项均为正数的数列的前n项和为Sn,已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且对一切都成立.
(1)若λ = 1,求数列的通项公式;
(2)求λ的值,使数列是等差数列.
【答案】(1)an = 2n1(2)λ = 0.
【解析】
( http: / / www.21cnjy.com )(2)令n = 1,得.令n = 2,得. ………………… 10分
要使数列是等差数列,必须有,解得λ = 0. ………………… 11分
当λ = 0时,,且.
当n≥2时,,
整理,得,, ………………… 13分
从而,
化简,得,所以. ……………… 15分
综上所述,(),
所以λ = 0时,数列是等差数列. ………………… 16分
考点:已知求
20.(本小题满分16分)
已知函数,其中m,a均为实数.
(1)求的极值;
(2)设,若对任意的 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,恒成立,求的最小值;
(3)设,若对任意给定的,在区间上总存在,使得 成立,求的取值范围.
( http: / / www.21cnjy.com )对于函数在上值域中每一个值,函数在上总有两个不同自变量与之对应相等.首先求出函数在上值域,然后根据函数在上必须不为单调函数且每段单调区间对应的值域都需包含.由在不单调得,由每段单调区间对应的值域都需包含得,.www.21-cn-jy.com
试题解析:(1),令,得x = 1. ………………… 1分
列表如下:
x (∞,1) 1 (1,∞)
0
g(x) ↗ 极大值 ↘
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
附加题
21.【选做题】在A、B、C、D 四小题中 ( http: / / www.21cnjy.com )只能选做两题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.2·1·c·n·j·y
21.A.选修4—1:几何证明选讲
如图,⊙ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为四边形 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的外接圆,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 延长线上一点,直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 相切.
求证: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
( http: / / www.21cnjy.com )
【答案】详见解析
【解析】
( http: / / www.21cnjy.com )
21.B.选修4—2:矩阵与变换
已知矩阵 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,计算 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
【答案】
【解析】
试题分析:利用矩阵特征值及其对应特征向量性质:进行化简.先根据矩阵M的特征多项式求出其特征值,进而求出对应的特征向量,.再将分解成特征向量,即,最后利用性质求结果,即 ( http: / / www.21cnjy.com )
21.C.选修4—4:坐标系与参数方程
在平面直角坐标系 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 中,圆的参数方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,以坐标原点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为极点,轴的正半
轴为极轴建立极坐标系.求:
(1)圆的直角坐标方程;
(2)圆的极坐标方程.
( http: / / www.21cnjy.com )21.D.选修4—5:不等式选讲
已知函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图象恒在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 轴上方,求实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围.
( http: / / www.21cnjy.com )
22.(本小题满分10分)
甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且各次投篮的结果互不影响.甲
同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的分布列和数学期望.
( http: / / www.21cnjy.com )(2)由题意.
,,,,
.
的分布表为
1 2 3 4 5
…………………8分
的数学期望. …………………10分
考点:概率分布,数学期望值
23.(本小题满分10分)
设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,其中当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为偶数时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为奇数时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
(1)证明:当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
