2022-2023学年数学人教版七年级下册6.1平方根培优同步练习题(含答案)
文档属性
| 名称 | 2022-2023学年数学人教版七年级下册6.1平方根培优同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 281.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 20:52:33 | ||
图片预览



文档简介
6.1 平方根 培优同步练习题
一、单选题 (本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知,则的值为( )
A. B. C. D.
2.下列等式一定成立的是( )
A. B. C. D.
3.的值是( )
A. B. C. D.
4.当x等于( )时,有最( )值.
A.2,小 B.2,大 C.±2,小 D.±2,大
5.某正数x的平方根为2+a和1﹣2a,则x的值为( )
A.3 B.5 C.15 D.25
6.下列命题:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③垂直于同一条直线的两条直线平行;④负数没有算术平方根;⑤平方根等于它本身的数是0和1.其中的假命题有( )
A.4个 B.3个 C.2个 D.1个
7.若 则( )
A.0.01732 B.0.1732 C.0.05477 D.0.5477
8.方程的解是( )
A. B.4或0 C.2 D.4
9.下列等式成立的是( )
A. B. C. D.
10.实数的算术平方根是( )
A. B. C. D.
填空题(本题共6小题,每小题4分,共24分
11.已知与互为相反数,则的值为___________.
12.若实数x、y、z满足,则____.
13.定义新运算“”:,则______.
14.一个正数的两个平方根是x+3与2x-6,则x=_________.
15.已知,,则__.
16.解方程:的解为________
三、解答题 本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.18-21题 每题8分 22题10分 23题10分 24题13分 25题13分
17.计算:
(1)
(2)
18.已知和是某一个正数的不同平方根,求这个正数.
19.先化简,再求值:,其中满足.
20.已知某正数的两个平方根是和,求这个正数.
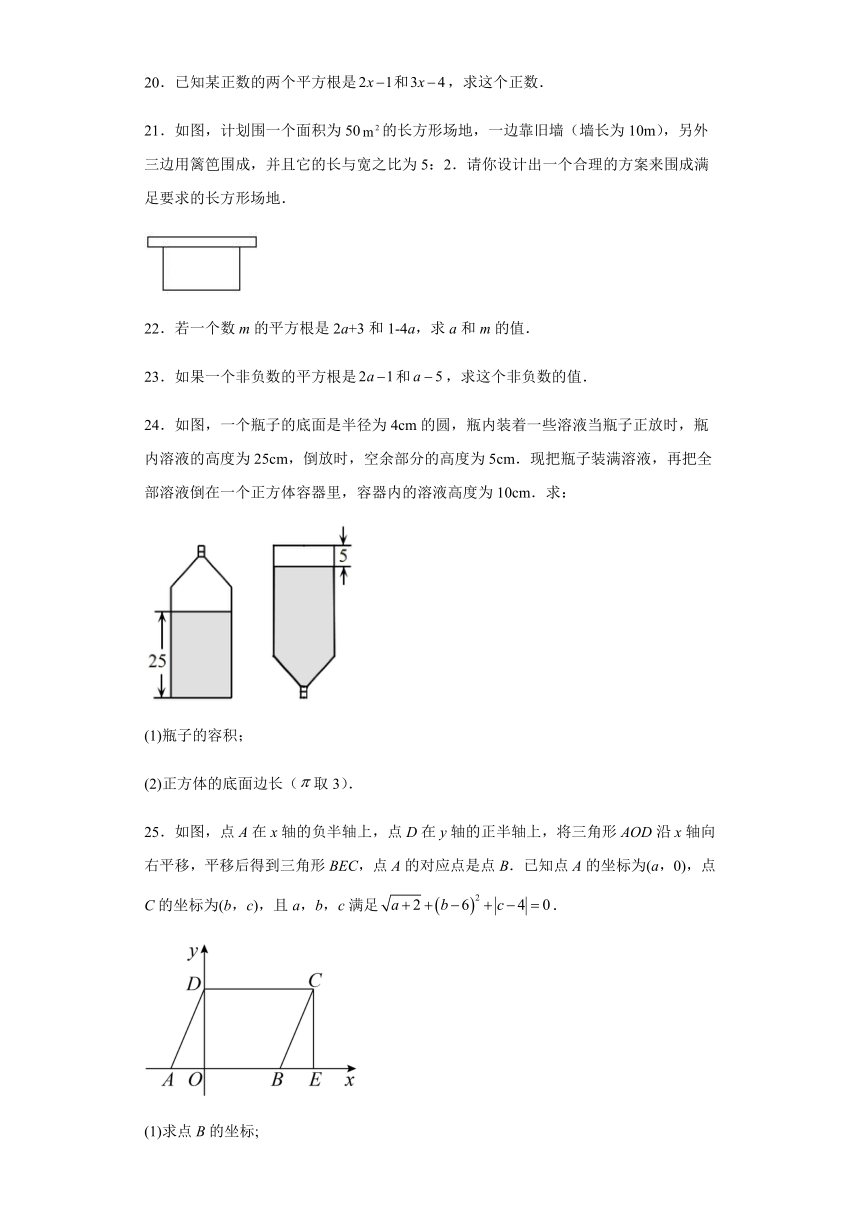
21.如图,计划围一个面积为50的长方形场地,一边靠旧墙(墙长为10m),另外三边用篱笆围成,并且它的长与宽之比为5:2.请你设计出一个合理的方案来围成满足要求的长方形场地.
22.若一个数m的平方根是2a+3和1-4a,求a和m的值.
23.如果一个非负数的平方根是和,求这个非负数的值.
24.如图,一个瓶子的底面是半径为4cm的圆,瓶内装着一些溶液当瓶子正放时,瓶内溶液的高度为25cm,倒放时,空余部分的高度为5cm.现把瓶子装满溶液,再把全部溶液倒在一个正方体容器里,容器内的溶液高度为10cm.求:
(1)瓶子的容积;
(2)正方体的底面边长(取3).
25.如图,点A在x轴的负半轴上,点D在y轴的正半轴上,将三角形AOD沿x轴向右平移,平移后得到三角形BEC,点A的对应点是点B.已知点A的坐标为(a,0),点C的坐标为(b,c),且a,b,c满足.
(1)求点B的坐标;
(2)求证:∠DAE=∠BCD;
(3)点P是线段BC上一动点(不与点B、C重合),连接DP、AP,在点P运动过程中,∠CDP、∠DPA、∠PAE之间是否存在永远不变的数量关系?若存在,写出它们之间的数量关系,并请证明;若不存在,请说明理由.
参考答案:
1.C
2.D
3.B
4.D
5.D
6.A
7.B
8.B
9.D
10.A
11.##
12.9
13.
14.1
15.0.228##
16.8或2##2或8
17.(1)
(2)
(2)将系数化为1,然后利用平方根的性质求解.
(1)
解:原式
;
(2)
.
18.4
【详解】解 正数的平方根为 和 ,
,
解这个方程得:.
当 时,,,
这个正数为 .
19.;
【详解】解:原式
,
,
,,
解得:,,
原式.
20.1
【详解】解:某正数的两个平方根是和,
,
解得,
则这个正数是.
21.长为m,宽为m
【详解】解:设长方形场地的长为5xm,宽为2xm,依题意,得,
,
解得:或(舍)
故长方形场地长为m,宽为m.
22.a=2,m=49
【详解】解:∵一个数m的平方根是2a+3和1-4a,
∴2a+3+1-4a=0,
解得:a=2,
∴.
23.这个非负数是9
【详解】解:∵一个非负数的平方根是2a-1和a-5,
∴(2a-1)+(a-5)=0,解得a=2,
∴2a-1=2×2-1=3,
∴这个非负数是32=9,
24.(1)
(2)
【详解】(1)解:∵瓶子的底面是半径为4cm的圆,
∴瓶子的底面积为:,
由题意可得,瓶子的容积与同底、高为的圆柱体积相等,
∴瓶子的容积为:,
即瓶子的容积为.
(2)解:由题意,正方形容器的底面积为:,
,
即正方体的底面边长为.
25.(1)B(4,0)
(2)见解析
(3)∠DPA=∠CDP+∠PAE,理由见解析
(1)
解得
已知点A的坐标为(a,0),点C的坐标为(b,c)
将三角形AOD沿x轴向右平移,平移后得到三角形BEC
(2)
∵三角形AOD沿x轴向右平移,平移后得到三角形BEC,
∴AD∥BC,CD∥AB
∴∠DAE=∠CBE ,∠CBE=∠BCD
∴∠DAE=∠BCD;
(3)
存在;∠DPA=∠CDP+∠PAE.
如图,过点P作PQ∥AB
∵CD∥AB,
∴PQ∥CD∥AB
∴∠CDP=∠DPQ,∠QPA=∠PAE
∴∠DPA=∠DPQ+∠QPA=∠CDP+∠PAE
一、单选题 (本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知,则的值为( )
A. B. C. D.
2.下列等式一定成立的是( )
A. B. C. D.
3.的值是( )
A. B. C. D.
4.当x等于( )时,有最( )值.
A.2,小 B.2,大 C.±2,小 D.±2,大
5.某正数x的平方根为2+a和1﹣2a,则x的值为( )
A.3 B.5 C.15 D.25
6.下列命题:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③垂直于同一条直线的两条直线平行;④负数没有算术平方根;⑤平方根等于它本身的数是0和1.其中的假命题有( )
A.4个 B.3个 C.2个 D.1个
7.若 则( )
A.0.01732 B.0.1732 C.0.05477 D.0.5477
8.方程的解是( )
A. B.4或0 C.2 D.4
9.下列等式成立的是( )
A. B. C. D.
10.实数的算术平方根是( )
A. B. C. D.
填空题(本题共6小题,每小题4分,共24分
11.已知与互为相反数,则的值为___________.
12.若实数x、y、z满足,则____.
13.定义新运算“”:,则______.
14.一个正数的两个平方根是x+3与2x-6,则x=_________.
15.已知,,则__.
16.解方程:的解为________
三、解答题 本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.18-21题 每题8分 22题10分 23题10分 24题13分 25题13分
17.计算:
(1)
(2)
18.已知和是某一个正数的不同平方根,求这个正数.
19.先化简,再求值:,其中满足.
20.已知某正数的两个平方根是和,求这个正数.
21.如图,计划围一个面积为50的长方形场地,一边靠旧墙(墙长为10m),另外三边用篱笆围成,并且它的长与宽之比为5:2.请你设计出一个合理的方案来围成满足要求的长方形场地.
22.若一个数m的平方根是2a+3和1-4a,求a和m的值.
23.如果一个非负数的平方根是和,求这个非负数的值.
24.如图,一个瓶子的底面是半径为4cm的圆,瓶内装着一些溶液当瓶子正放时,瓶内溶液的高度为25cm,倒放时,空余部分的高度为5cm.现把瓶子装满溶液,再把全部溶液倒在一个正方体容器里,容器内的溶液高度为10cm.求:
(1)瓶子的容积;
(2)正方体的底面边长(取3).
25.如图,点A在x轴的负半轴上,点D在y轴的正半轴上,将三角形AOD沿x轴向右平移,平移后得到三角形BEC,点A的对应点是点B.已知点A的坐标为(a,0),点C的坐标为(b,c),且a,b,c满足.
(1)求点B的坐标;
(2)求证:∠DAE=∠BCD;
(3)点P是线段BC上一动点(不与点B、C重合),连接DP、AP,在点P运动过程中,∠CDP、∠DPA、∠PAE之间是否存在永远不变的数量关系?若存在,写出它们之间的数量关系,并请证明;若不存在,请说明理由.
参考答案:
1.C
2.D
3.B
4.D
5.D
6.A
7.B
8.B
9.D
10.A
11.##
12.9
13.
14.1
15.0.228##
16.8或2##2或8
17.(1)
(2)
(2)将系数化为1,然后利用平方根的性质求解.
(1)
解:原式
;
(2)
.
18.4
【详解】解 正数的平方根为 和 ,
,
解这个方程得:.
当 时,,,
这个正数为 .
19.;
【详解】解:原式
,
,
,,
解得:,,
原式.
20.1
【详解】解:某正数的两个平方根是和,
,
解得,
则这个正数是.
21.长为m,宽为m
【详解】解:设长方形场地的长为5xm,宽为2xm,依题意,得,
,
解得:或(舍)
故长方形场地长为m,宽为m.
22.a=2,m=49
【详解】解:∵一个数m的平方根是2a+3和1-4a,
∴2a+3+1-4a=0,
解得:a=2,
∴.
23.这个非负数是9
【详解】解:∵一个非负数的平方根是2a-1和a-5,
∴(2a-1)+(a-5)=0,解得a=2,
∴2a-1=2×2-1=3,
∴这个非负数是32=9,
24.(1)
(2)
【详解】(1)解:∵瓶子的底面是半径为4cm的圆,
∴瓶子的底面积为:,
由题意可得,瓶子的容积与同底、高为的圆柱体积相等,
∴瓶子的容积为:,
即瓶子的容积为.
(2)解:由题意,正方形容器的底面积为:,
,
即正方体的底面边长为.
25.(1)B(4,0)
(2)见解析
(3)∠DPA=∠CDP+∠PAE,理由见解析
(1)
解得
已知点A的坐标为(a,0),点C的坐标为(b,c)
将三角形AOD沿x轴向右平移,平移后得到三角形BEC
(2)
∵三角形AOD沿x轴向右平移,平移后得到三角形BEC,
∴AD∥BC,CD∥AB
∴∠DAE=∠CBE ,∠CBE=∠BCD
∴∠DAE=∠BCD;
(3)
存在;∠DPA=∠CDP+∠PAE.
如图,过点P作PQ∥AB
∵CD∥AB,
∴PQ∥CD∥AB
∴∠CDP=∠DPQ,∠QPA=∠PAE
∴∠DPA=∠DPQ+∠QPA=∠CDP+∠PAE
