3.12《整理与复习》、《练习十》(课件)-五年级下册数学人教版(共22张PPT)
文档属性
| 名称 | 3.12《整理与复习》、《练习十》(课件)-五年级下册数学人教版(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 24.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 21:06:12 | ||
图片预览





文档简介
(共22张PPT)
人教版数学五年级下册
3
长方体和正方体
整理和复习&练习十
一、学习目标
1.掌握长方体和正方体的特征,表面积、体积、容积的概念以及相邻单位间的进率。
2.认识长方体和正方体的展开图,掌握长方体和正方体的表面积、体积、容积的计算方法,并灵活运用到实际生活中去。
长方体和正方体
01
长方体和正方体的认识
02
长方体和正方体的表面积
03
长方体和正方体的体积
展开图
表面积的计算
体积单位及换算
长方体、正方体的体积
容积和容积单位
不规则物体体积
二、整体回顾
本单元学习了关于长方体和正方体的哪些知识?
各部分的名称
表面积
体积(体积单位)
你能在图中分别标出长度相等的棱、大小相等的面吗?
三、知识梳理
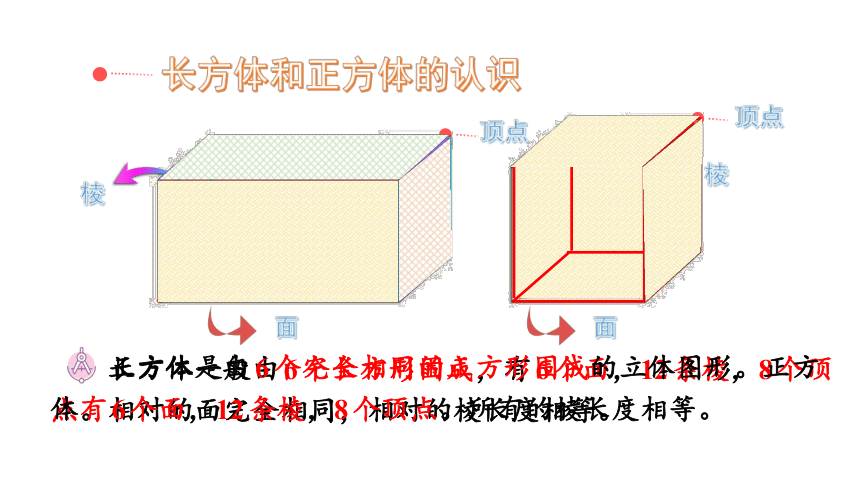
长方体一般由6个长方形围成,有6个面,12条棱,8个顶点。相对的面完全相同,相对的棱长度相等。
正方体是由6个完全相同的正方形围成的立体图形。正方体有6个面,12条棱,8个顶点。所有的棱长度相等。
长方体和正方体的认识
棱
棱
顶点
顶点
面
面
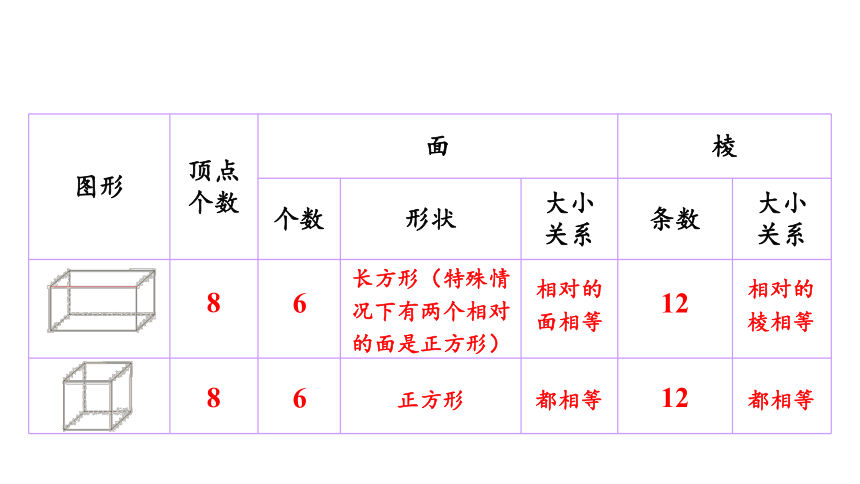
图形 顶点个数 面 棱 个数 形状 大小关系 条数 大小关系
8
6
长方形(特殊情况下有两个相对的面是正方形)
相对的面相等
12
相对的棱相等
8
6
正方形
都相等
12
都相等
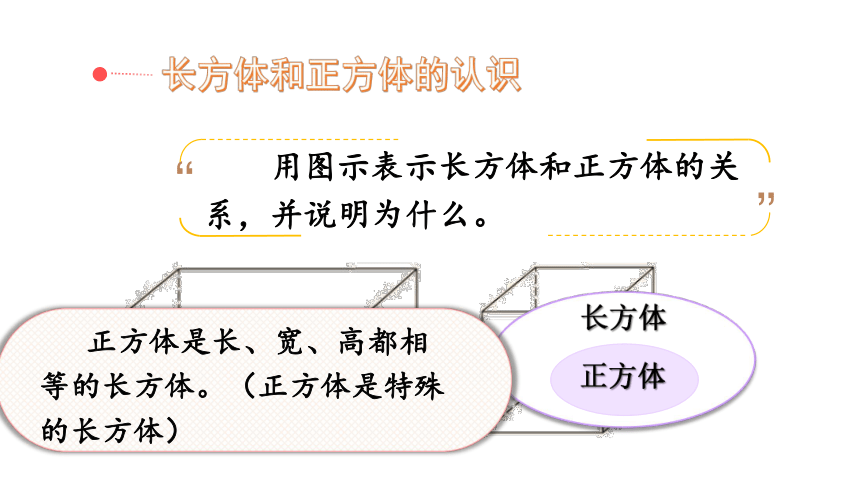
长方体和正方体的认识
”
用图示表示长方体和正方体的关系,并说明为什么。
“
长方体
正方体
正方体是长、宽、高都相等的长方体。(正方体是特殊的长方体)
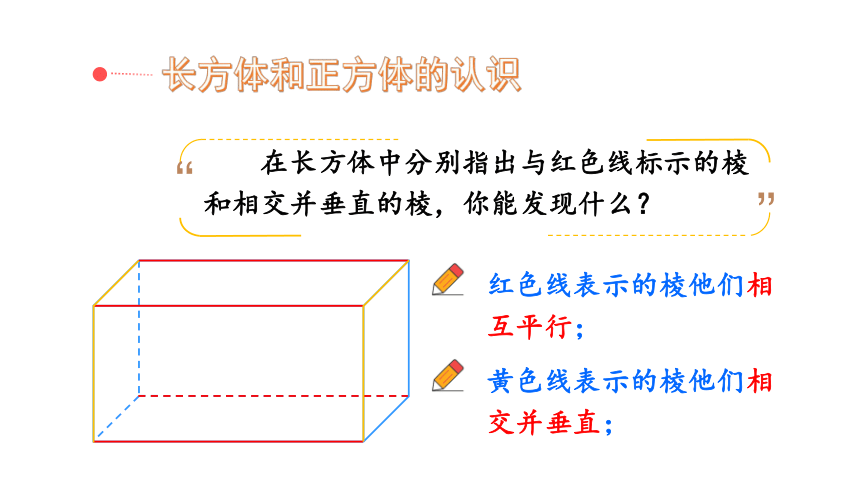
长方体和正方体的认识
”
在长方体中分别指出与红色线标示的棱和相交并垂直的棱,你能发现什么?
“
红色线表示的棱他们相互平行;
黄色线表示的棱他们相交并垂直;
本单元学习了关于长方体和正方体的哪些知识?
各部分的名称
表面积
体积(体积单位)
回忆计算表面积的方法以及探索体积公式的过程,想一想关键是要知道什么。
长方体展开图
后
上
前
下
左
右
正方体展开图
后
上
前
下
左
右
长方体和正方体的表面积
长方体为表面积是6个长方形面积之和。
正方体为表面积是6个正方形面积之和。
长方体和正方体的表面积
长(a)
宽(b)
高(h)
(长×宽+长×高+宽×高)×2
S表=(ab+ah+bh)×2
棱(a)
棱(a)
棱(a)
棱长×棱长×6
S表=6a
计算物体的表面积,关键要知道物体的长、宽、高这三个量;
本单元学习了关于长方体和正方体的哪些知识?
各部分的名称
表面积
体积(体积单位)
思考一下,计算体积的需要知道哪些关键信息,计算体积和容积有什么相同点?
长方体和正方体的体积
长度单位
厘米
分米
米
面积单位
平方厘米
平方分米
平方米
体积单位
立方厘米
立方分米
立方米
10
10
100
100
1000
1000
长方体和正方体的体积
长
宽
高
长方体的体积=长×宽×高
V = abh
正方体的体积=棱长×棱长×棱长
V = a3
底面积
长方体或正方体的体积=底面积×高
V = Sh
表面积 体积 容积
意义 长方体或正方体6个面的总面积 物体所占空间的大小 容器所能容纳物体体积的大小
计算方法 S长=(ab+ah+bh)×2 S正=a2×6 V长=abh V正=a3 V=sh 同体积
计量单位 m dm cm m dm cm m dm cm
L ml
单位间进率 1m =100dm 1dm =100cm 1m =1000dm 1dm =1000cm 1L=1000ml
1dm =1L
1cm =1ml
长方体和正方体的体积
你能用尺子和长方体(或正方体)容器测出下面物体的体积吗?如果用这种方法比较两个物体体积的大小,你打算怎样做?
玻璃球
绿豆
排水法
用排水法测量不规则物体的体积需要利用量筒或量杯记录下放入不规则物体前后水位的刻度,水面上升的部分水的体积就是不规则的物体的体积。
不规则物体体积=水面上升后的体积 水面上升前的体积
长方体和正方体的体积
1L=1000mL 1L=1dm 1mL=1cm
要求体积需要知道长方体的长、宽、高;
计算形状规范的容积时,与计算体积的方法一样,求不规范物体的容积,可以用排水法,具体情况具体对待。
长方体和正方体的体积
下面的长方体都是用棱长1cm的小正方体摆成的。算出它们的体积。
4cm
3cm
3cm
3×3×4=36(cm3)
4cm
4cm
4cm
4×4×4=64(cm3)
(教科书第43页练习十)
1.
下面是同一个长方体的展开图,说一说每个图是怎样展开的。
找一些正方体纸盒并将其展开,你能展开成多少种不同的形状?
四、巩固练习
2.
长方体的长、宽、高都变为原来的2倍,它的表面积和体积都发生了什么变化?
你发现了什么规律?
长 宽 高 表面积 体积
1 2cm 1cm 3cm cm cm
2 4cm 2cm 6cm cm cm
3 8cm 4cm 12cm cm cm
22
88
352
6
48
384
发现:表面积变为原来的4倍,体积变
为原来的8倍。
3.
一个长方体鱼塘长8m,宽4.5m,深2m。这个鱼塘的容积大约是多少?
8×4.5×2=72(m )
答:这个鱼塘的容积大约是72m 。
4.
某古建筑景点定做了25个宫灯形的垃圾桶(如图)。垃圾桶外侧有一层外饰面。如果外饰面每平方米180元,这些垃圾桶的外饰面一共要花多少钱?
46×80×4+66×20×4
答:这些垃圾桶的外饰面一共要花9000元钱。
=14720+5280
=20000(cm )
=2m
2×25×180=9000(元)
人教版数学五年级下册
3
长方体和正方体
整理和复习&练习十
一、学习目标
1.掌握长方体和正方体的特征,表面积、体积、容积的概念以及相邻单位间的进率。
2.认识长方体和正方体的展开图,掌握长方体和正方体的表面积、体积、容积的计算方法,并灵活运用到实际生活中去。
长方体和正方体
01
长方体和正方体的认识
02
长方体和正方体的表面积
03
长方体和正方体的体积
展开图
表面积的计算
体积单位及换算
长方体、正方体的体积
容积和容积单位
不规则物体体积
二、整体回顾
本单元学习了关于长方体和正方体的哪些知识?
各部分的名称
表面积
体积(体积单位)
你能在图中分别标出长度相等的棱、大小相等的面吗?
三、知识梳理
长方体一般由6个长方形围成,有6个面,12条棱,8个顶点。相对的面完全相同,相对的棱长度相等。
正方体是由6个完全相同的正方形围成的立体图形。正方体有6个面,12条棱,8个顶点。所有的棱长度相等。
长方体和正方体的认识
棱
棱
顶点
顶点
面
面
图形 顶点个数 面 棱 个数 形状 大小关系 条数 大小关系
8
6
长方形(特殊情况下有两个相对的面是正方形)
相对的面相等
12
相对的棱相等
8
6
正方形
都相等
12
都相等
长方体和正方体的认识
”
用图示表示长方体和正方体的关系,并说明为什么。
“
长方体
正方体
正方体是长、宽、高都相等的长方体。(正方体是特殊的长方体)
长方体和正方体的认识
”
在长方体中分别指出与红色线标示的棱和相交并垂直的棱,你能发现什么?
“
红色线表示的棱他们相互平行;
黄色线表示的棱他们相交并垂直;
本单元学习了关于长方体和正方体的哪些知识?
各部分的名称
表面积
体积(体积单位)
回忆计算表面积的方法以及探索体积公式的过程,想一想关键是要知道什么。
长方体展开图
后
上
前
下
左
右
正方体展开图
后
上
前
下
左
右
长方体和正方体的表面积
长方体为表面积是6个长方形面积之和。
正方体为表面积是6个正方形面积之和。
长方体和正方体的表面积
长(a)
宽(b)
高(h)
(长×宽+长×高+宽×高)×2
S表=(ab+ah+bh)×2
棱(a)
棱(a)
棱(a)
棱长×棱长×6
S表=6a
计算物体的表面积,关键要知道物体的长、宽、高这三个量;
本单元学习了关于长方体和正方体的哪些知识?
各部分的名称
表面积
体积(体积单位)
思考一下,计算体积的需要知道哪些关键信息,计算体积和容积有什么相同点?
长方体和正方体的体积
长度单位
厘米
分米
米
面积单位
平方厘米
平方分米
平方米
体积单位
立方厘米
立方分米
立方米
10
10
100
100
1000
1000
长方体和正方体的体积
长
宽
高
长方体的体积=长×宽×高
V = abh
正方体的体积=棱长×棱长×棱长
V = a3
底面积
长方体或正方体的体积=底面积×高
V = Sh
表面积 体积 容积
意义 长方体或正方体6个面的总面积 物体所占空间的大小 容器所能容纳物体体积的大小
计算方法 S长=(ab+ah+bh)×2 S正=a2×6 V长=abh V正=a3 V=sh 同体积
计量单位 m dm cm m dm cm m dm cm
L ml
单位间进率 1m =100dm 1dm =100cm 1m =1000dm 1dm =1000cm 1L=1000ml
1dm =1L
1cm =1ml
长方体和正方体的体积
你能用尺子和长方体(或正方体)容器测出下面物体的体积吗?如果用这种方法比较两个物体体积的大小,你打算怎样做?
玻璃球
绿豆
排水法
用排水法测量不规则物体的体积需要利用量筒或量杯记录下放入不规则物体前后水位的刻度,水面上升的部分水的体积就是不规则的物体的体积。
不规则物体体积=水面上升后的体积 水面上升前的体积
长方体和正方体的体积
1L=1000mL 1L=1dm 1mL=1cm
要求体积需要知道长方体的长、宽、高;
计算形状规范的容积时,与计算体积的方法一样,求不规范物体的容积,可以用排水法,具体情况具体对待。
长方体和正方体的体积
下面的长方体都是用棱长1cm的小正方体摆成的。算出它们的体积。
4cm
3cm
3cm
3×3×4=36(cm3)
4cm
4cm
4cm
4×4×4=64(cm3)
(教科书第43页练习十)
1.
下面是同一个长方体的展开图,说一说每个图是怎样展开的。
找一些正方体纸盒并将其展开,你能展开成多少种不同的形状?
四、巩固练习
2.
长方体的长、宽、高都变为原来的2倍,它的表面积和体积都发生了什么变化?
你发现了什么规律?
长 宽 高 表面积 体积
1 2cm 1cm 3cm cm cm
2 4cm 2cm 6cm cm cm
3 8cm 4cm 12cm cm cm
22
88
352
6
48
384
发现:表面积变为原来的4倍,体积变
为原来的8倍。
3.
一个长方体鱼塘长8m,宽4.5m,深2m。这个鱼塘的容积大约是多少?
8×4.5×2=72(m )
答:这个鱼塘的容积大约是72m 。
4.
某古建筑景点定做了25个宫灯形的垃圾桶(如图)。垃圾桶外侧有一层外饰面。如果外饰面每平方米180元,这些垃圾桶的外饰面一共要花多少钱?
46×80×4+66×20×4
答:这些垃圾桶的外饰面一共要花9000元钱。
=14720+5280
=20000(cm )
=2m
2×25×180=9000(元)
