1.5.1《有理数的乘方》课件
文档属性
| 名称 | 1.5.1《有理数的乘方》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 988.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-19 12:19:16 | ||
图片预览







文档简介
课件20张PPT。1.5.1有理数的乘方学.科.网
一根面对折过来拉一次得 2 根面条第二次对折过来拉一次得2×2 =4 根面条第三次对折过来拉一次得2×2×2=8根面条......第七次对折过来拉一次得2×2×2×2×2×2×2=128 根面条学.科.网
情境创设我们知道多个数相加,如:
2+2+2可以记作: 2×32+2+2+2可以记作:2×4那么3个2相乘该怎么记呢?3个2相乘我们可以记作:237个2相乘可以记作:27学.科.网
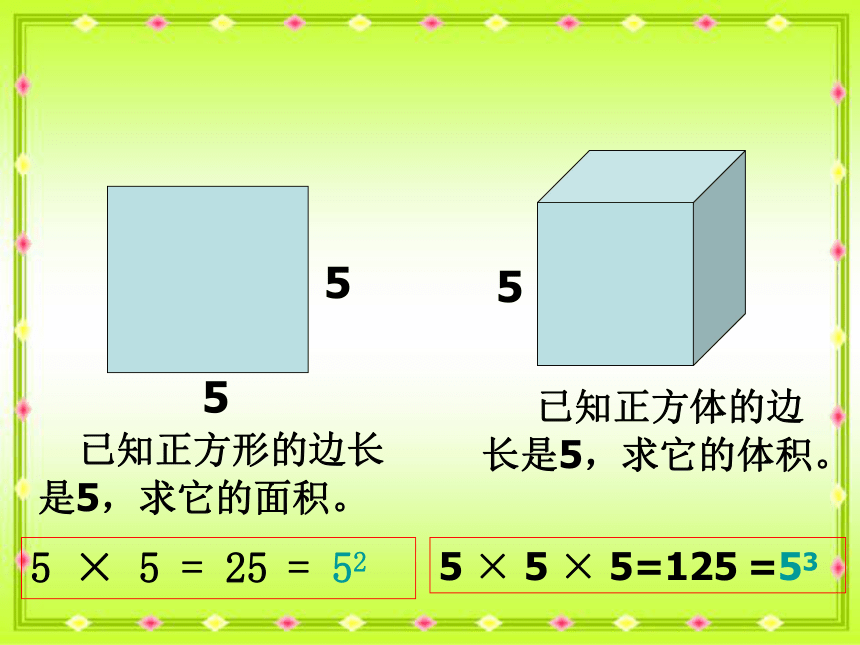
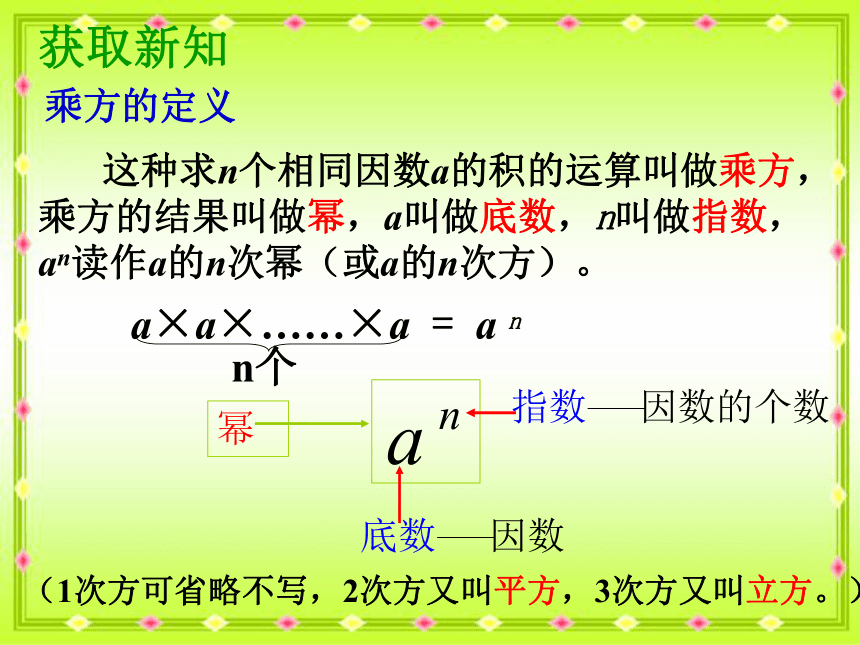
55 已知正方形的边长是5,求它的面积。5 × 5 = 255 已知正方体的边长是5,求它的体积。5 × 5 × 5=125= 52=53乘方的定义 这种求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂,a叫做底数,n叫做指数,an读作a的n次幂(或a的n次方)。 (1次方可省略不写,2次方又叫平方,3次方又叫立方。)获取新知填一填777底数指数-310-3-310巩固新知:1、(口答)
把下列相同因数的乘积
写成幂的形式,并说出底数和指数:(1) (-6)×(-6) ×(-6)底数是 –6,指数是 3(2)底数是指数是 4温馨提示:幂的底数是分数或负数时,底数应该添上括号!(3) (-5)4 与 -54对于分数的乘方,负数的乘方,书写时一定要注意小括号。 2、把 写成几个相同因数相乘的形式3、把(-2)× (-2)× (-2)×···×(-2)10个(-2)写成幂的形式。例1 计算:(1) 53 (2)05
(3)(-4)3 (4) (-2)4
(5) (- )5 (6)(- )2你能得到什么规律?规律:
正数的任何次幂都是正数;
负数的奇次幂是负数;
负数的偶次幂是正数;
0的任何正整数次幂都是0。猜一猜例2 计算:
–32; (4)8 ÷(-2)3×(-2.5)
(2) 3 × 23;
(3)(3 × 2)3;
解:原式=-(3×3)=-9解:原式=3 ×8=24解:原式=63=216解:原式=8 ÷(-8)×(-2.5)=2.5先算乘方,后算乘除;
如果遇到括号就先进行括号里的运算。思考:通过以上计算,
对于乘除和乘方的混合运算,
你觉得有怎样的运算顺序?运用新知 体会成功: (1)、(-5)3 (2)、
(3)、5×23 (4)、(5×2)3
(5)、(-2)2 ×(-3)2
(6)、(-2)3÷ 22 -12540100036-2细胞分裂问题:
某种细胞每过30分钟便由1个分裂成2个。经过3小时,这种细胞由1个能分裂成多少个?应用分析:2(个)2×2×2=8(个)<二次 >1个小时后:<一次>1个细胞30分后:2×2=4(个)<三次> 1.5个小时后:…………<六次>3个小时后:这节课你学会了一种什么运算?你有何体会?(2)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.分数的乘方,在书写的时一定要把整个分数用小括号括起来.(1)正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.小结作业:A组:课本47页复习巩固第1题
B组:练习册41页第11题1-8小题。 古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗? 事实上,按照这个大臣的要求,放满一个棋盘上的64个格子需要1+22+23+……+263=264-1粒米。 264到底多大呢?
答案是:18 446 744 073 709 551 616读一读
棋盘上的学问按每千粒米40克计算共需737869762948吨拓展珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰。这是真的吗?≈ ≈ 解:对折30次后的厚度为折叠30次后的厚度超过珠穆朗玛峰反思“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
一根面对折过来拉一次得 2 根面条第二次对折过来拉一次得2×2 =4 根面条第三次对折过来拉一次得2×2×2=8根面条......第七次对折过来拉一次得2×2×2×2×2×2×2=128 根面条学.科.网
情境创设我们知道多个数相加,如:
2+2+2可以记作: 2×32+2+2+2可以记作:2×4那么3个2相乘该怎么记呢?3个2相乘我们可以记作:237个2相乘可以记作:27学.科.网
55 已知正方形的边长是5,求它的面积。5 × 5 = 255 已知正方体的边长是5,求它的体积。5 × 5 × 5=125= 52=53乘方的定义 这种求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂,a叫做底数,n叫做指数,an读作a的n次幂(或a的n次方)。 (1次方可省略不写,2次方又叫平方,3次方又叫立方。)获取新知填一填777底数指数-310-3-310巩固新知:1、(口答)
把下列相同因数的乘积
写成幂的形式,并说出底数和指数:(1) (-6)×(-6) ×(-6)底数是 –6,指数是 3(2)底数是指数是 4温馨提示:幂的底数是分数或负数时,底数应该添上括号!(3) (-5)4 与 -54对于分数的乘方,负数的乘方,书写时一定要注意小括号。 2、把 写成几个相同因数相乘的形式3、把(-2)× (-2)× (-2)×···×(-2)10个(-2)写成幂的形式。例1 计算:(1) 53 (2)05
(3)(-4)3 (4) (-2)4
(5) (- )5 (6)(- )2你能得到什么规律?规律:
正数的任何次幂都是正数;
负数的奇次幂是负数;
负数的偶次幂是正数;
0的任何正整数次幂都是0。猜一猜例2 计算:
–32; (4)8 ÷(-2)3×(-2.5)
(2) 3 × 23;
(3)(3 × 2)3;
解:原式=-(3×3)=-9解:原式=3 ×8=24解:原式=63=216解:原式=8 ÷(-8)×(-2.5)=2.5先算乘方,后算乘除;
如果遇到括号就先进行括号里的运算。思考:通过以上计算,
对于乘除和乘方的混合运算,
你觉得有怎样的运算顺序?运用新知 体会成功: (1)、(-5)3 (2)、
(3)、5×23 (4)、(5×2)3
(5)、(-2)2 ×(-3)2
(6)、(-2)3÷ 22 -12540100036-2细胞分裂问题:
某种细胞每过30分钟便由1个分裂成2个。经过3小时,这种细胞由1个能分裂成多少个?应用分析:2(个)2×2×2=8(个)<二次 >1个小时后:<一次>1个细胞30分后:2×2=4(个)<三次> 1.5个小时后:…………<六次>3个小时后:这节课你学会了一种什么运算?你有何体会?(2)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.分数的乘方,在书写的时一定要把整个分数用小括号括起来.(1)正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.小结作业:A组:课本47页复习巩固第1题
B组:练习册41页第11题1-8小题。 古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗? 事实上,按照这个大臣的要求,放满一个棋盘上的64个格子需要1+22+23+……+263=264-1粒米。 264到底多大呢?
答案是:18 446 744 073 709 551 616读一读
棋盘上的学问按每千粒米40克计算共需737869762948吨拓展珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰。这是真的吗?≈ ≈ 解:对折30次后的厚度为折叠30次后的厚度超过珠穆朗玛峰反思“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
