2022-2023学年 北师大版九年级数学下册1.5三角函数的应用课后综合练习(无答案)
文档属性
| 名称 | 2022-2023学年 北师大版九年级数学下册1.5三角函数的应用课后综合练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 727.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-12 00:00:00 | ||
图片预览

文档简介
北师大版九年级数学下册1.5三角函数的应用课后综合练习
一、单选题
1、如图,已知窗户高米,窗户外面上方0.2米的点C处安装水平遮阳板米,当太阳光线与水平线成α角时,光线刚好不能直接射入室内,则的关系式是( )
A.n=mtanα-0.2 B.n=mtanα+0.2
C.m=ntanα-0.2 D.m=ntanα+0.2
2、如图为北京冬奥会“雪飞天”滑雪大跳台赛道.若点A的高AE=a米,水平赛道BC=b米,赛道AB,CD的坡角均为θ,则点D与点A的水平距离DE为( )
米 B.( b)米 C.(a-b)sinθ米 D.(a﹣b)cosθ米
3、已知α是锐角,cosα=,则tanα的值是( )
A. B.2 C.3 D.
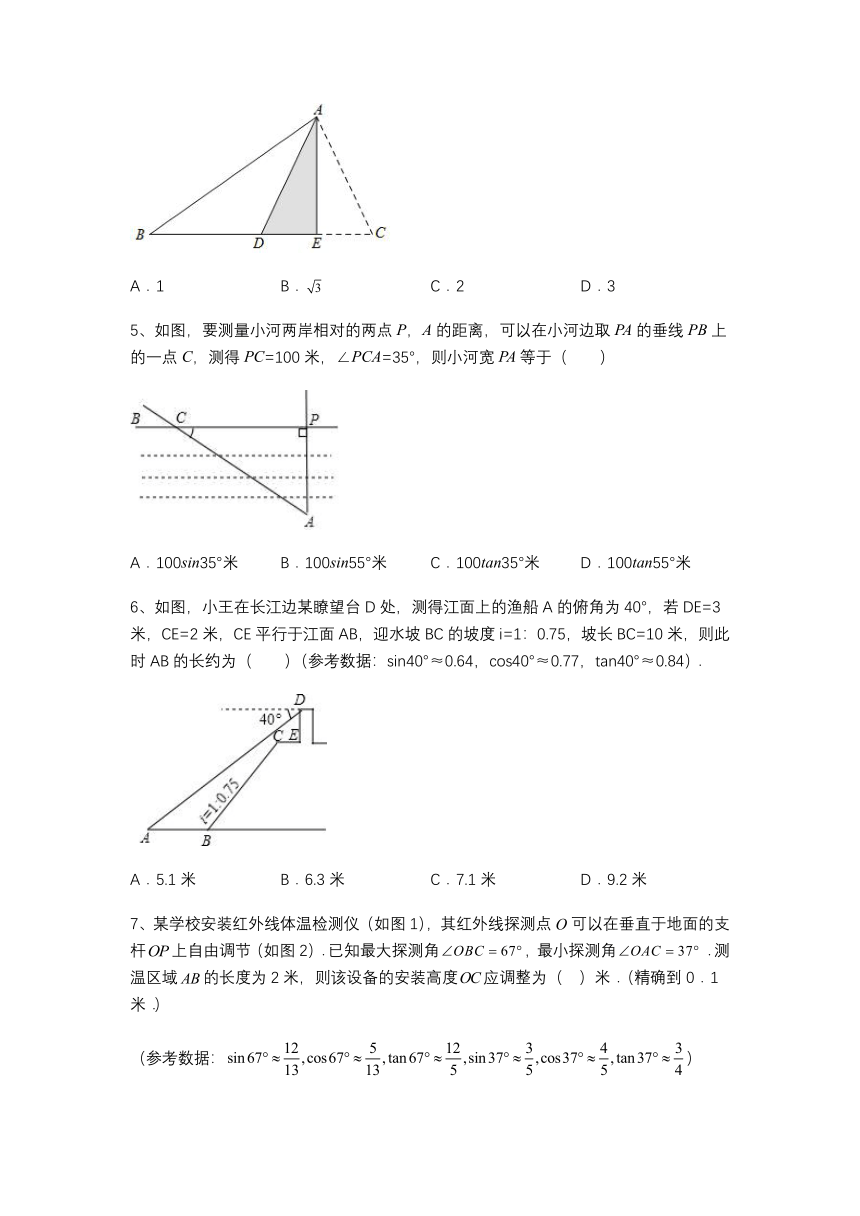
4、如图,在△ABC中,点D在BC上,且AD=BD=CD,AE是BC边上的高,若沿AE所在直线折叠,点C恰好落在点D处,若AB=,则△ADC的周长等于( )
A.1 B. C.2 D.3
5、如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )
A.100sin35°米 B.100sin55°米 C.100tan35°米 D.100tan55°米
6、如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
A.5.1米 B.6.3米 C.7.1米 D.9.2米
7、某学校安装红外线体温检测仪(如图1),其红外线探测点O可以在垂直于地面的支杆上自由调节(如图2).已知最大探测角,最小探测角.测温区域的长度为2米,则该设备的安装高度应调整为( )米.(精确到0.1米.)
(参考数据:)
A.2.4 B.2.2 C.3.0 D.2.7
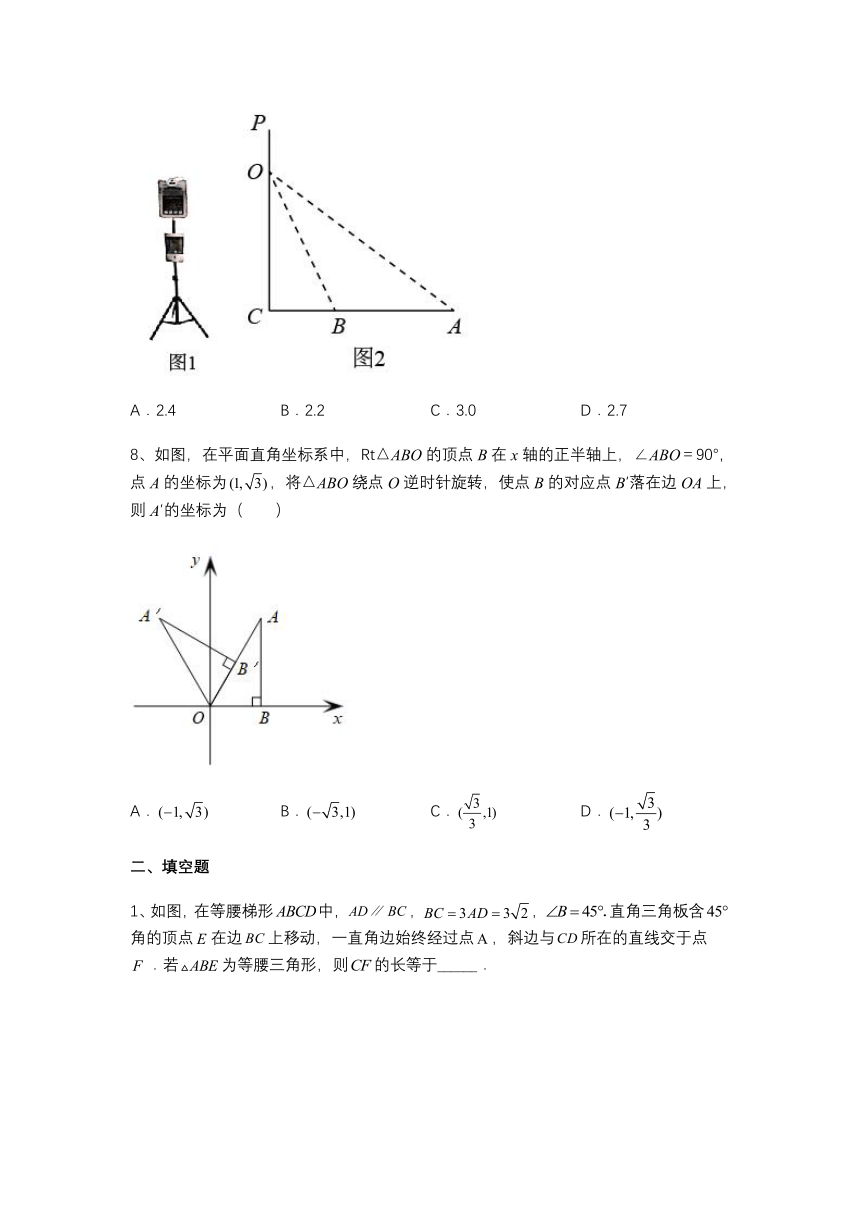
8、如图,在平面直角坐标系中,Rt△ABO的顶点B在x轴的正半轴上,∠ABO=90°,点A的坐标为,将△ABO绕点O逆时针旋转,使点B的对应点B′落在边OA上,则A′的坐标为( )
A. B. C. D.
二、填空题
1、如图,在等腰梯形中,,,直角三角板含角的顶点在边上移动,一直角边始终经过点,斜边与所在的直线交于点.若为等腰三角形,则的长等于______.
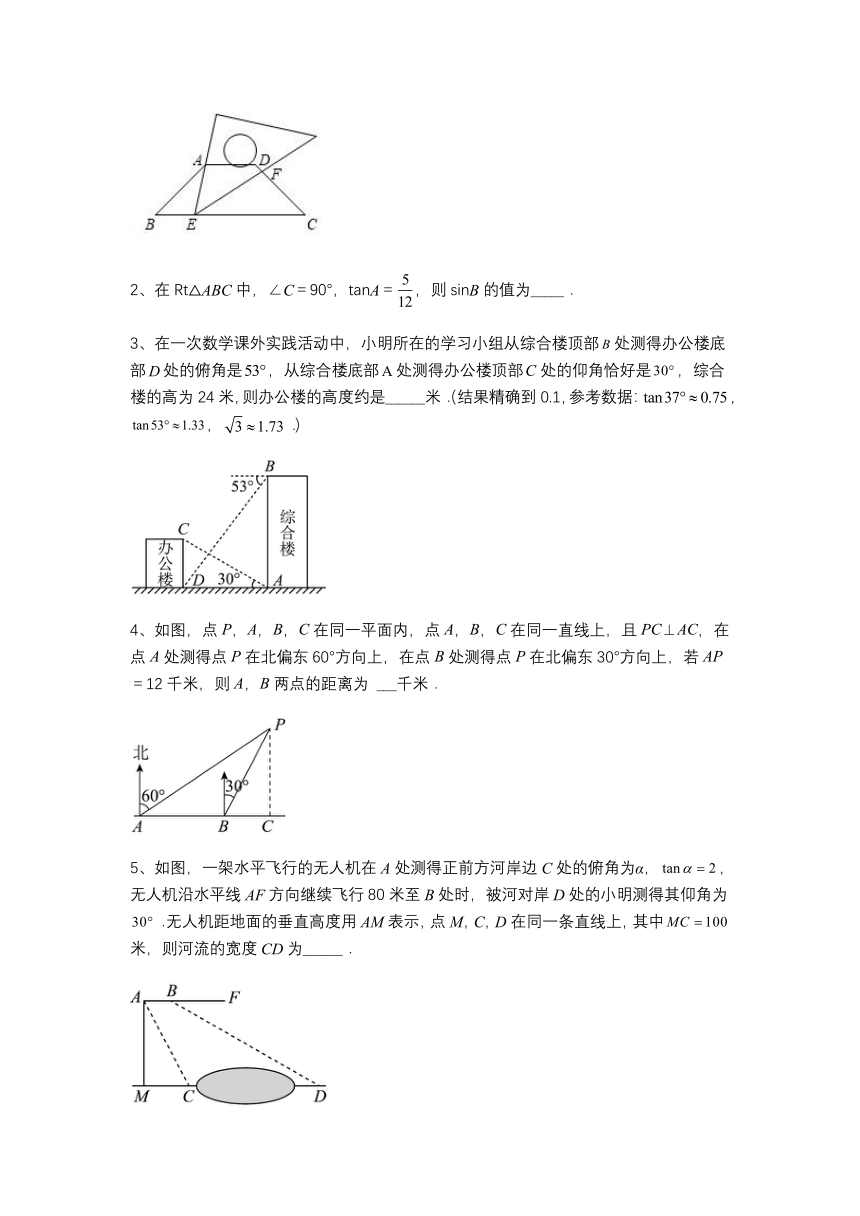
2、在Rt△ABC中,∠C=90°,tanA=,则sinB的值为_____.
3、在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部处测得办公楼底部处的俯角是,从综合楼底部处测得办公楼顶部处的仰角恰好是,综合楼的高为24米,则办公楼的高度约是______米.(结果精确到0.1,参考数据:,,.)
4、如图,点P,A,B,C在同一平面内,点A,B,C在同一直线上,且PC⊥AC,在点A处测得点P在北偏东60°方向上,在点B处测得点P在北偏东30°方向上,若AP=12千米,则A,B两点的距离为 ___千米.
5、如图,一架水平飞行的无人机在A处测得正前方河岸边C处的俯角为α,,无人机沿水平线AF方向继续飞行80米至B处时,被河对岸D处的小明测得其仰角为.无人机距地面的垂直高度用AM表示,点M,C,D在同一条直线上,其中米,则河流的宽度CD为______.
6、小明用一块含有角()的直角三角尺测量校园内某棵树的高度,示意图如图所示.若小明的眼睛与地面之间的垂直高度为,小明与树之间的水平距离为,则这棵树的高度约为______.(结果精确到,参考数据:)
三、解答题
1、如图,-楼房AB后有一-假山CD,CD的坡度为,测得B与C的距离为24米,山坡坡面上E点处有一休息亭,与山脚C的距离米,小丽从楼房房顶A处测得E的俯角为45°.
(1)求点E到水平地面的距离;
(2)求楼房AB的高.
2、如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面,坡角.在阳光下,小明观察到在地面上的影长为,在坡面上的影长为.同一时刻,小明测得直立于地面长60cm的木杆的影长为90cm(其影子完全落在地面上).求立柱AB的高度.
3、如图,小华利用标杆和等腰直角三角尺测量楼高,他先在E处竖立一根高1.5米的标杆DE,发现地面上的点A、标杆顶端D与楼顶B在一条直线上,测得米;然后他站在F处利用等腰直角三角形测得视线GB与水平面的夹角,小华的眼睛到地面的距离米,米.已知点F、A、E、C在同一直线上,,,.请根据以上所测数据,计算楼高BC.
4、湖中小岛上码头C处一名游客突发疾病,需要救援.位于湖面B点处的快艇和湖岸A处的救援船接到通知后立刻同时出发前往救援.计划由快艇赶到码头C接该游客,再沿方向行驶,与救援船相遇后将该游客转运到救援船上.已知C在A的北偏东30°方向上,B在A的北偏东60°方向上,且B在C的正南方向900米处.
(1)求湖岸A与码头C的距离(结果精确到1米,参考数据:);
(2)救援船的平均速度为150米/分,快艇的平均速度为400米/分,在接到通知后,快艇能否在5分钟内将该游客送上救援船?请说明理由.(接送游客上下船的时间忽略不计)
5、如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边AB、BC于点D、E,连结AE.
(1)如果∠B=25°,求∠CAE的度数;
(2)如果CE=2,,求的值.
6、如图,株洲市炎陵县某中学在实施“五项管理”中,将学校的“五项管理”做成宣传牌(CD),放置在教学楼A栋的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿芙蓉小学围墙边坡AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:3,AB=2m,AE=8m.
(1)求点B距水平面AE的高度BH.
(2)求宣传牌CD的高度.(结果精确到0.1米.参考数据:≈1.414 ,≈1.732 )
一、单选题
1、如图,已知窗户高米,窗户外面上方0.2米的点C处安装水平遮阳板米,当太阳光线与水平线成α角时,光线刚好不能直接射入室内,则的关系式是( )
A.n=mtanα-0.2 B.n=mtanα+0.2
C.m=ntanα-0.2 D.m=ntanα+0.2
2、如图为北京冬奥会“雪飞天”滑雪大跳台赛道.若点A的高AE=a米,水平赛道BC=b米,赛道AB,CD的坡角均为θ,则点D与点A的水平距离DE为( )
米 B.( b)米 C.(a-b)sinθ米 D.(a﹣b)cosθ米
3、已知α是锐角,cosα=,则tanα的值是( )
A. B.2 C.3 D.
4、如图,在△ABC中,点D在BC上,且AD=BD=CD,AE是BC边上的高,若沿AE所在直线折叠,点C恰好落在点D处,若AB=,则△ADC的周长等于( )
A.1 B. C.2 D.3
5、如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )
A.100sin35°米 B.100sin55°米 C.100tan35°米 D.100tan55°米
6、如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
A.5.1米 B.6.3米 C.7.1米 D.9.2米
7、某学校安装红外线体温检测仪(如图1),其红外线探测点O可以在垂直于地面的支杆上自由调节(如图2).已知最大探测角,最小探测角.测温区域的长度为2米,则该设备的安装高度应调整为( )米.(精确到0.1米.)
(参考数据:)
A.2.4 B.2.2 C.3.0 D.2.7
8、如图,在平面直角坐标系中,Rt△ABO的顶点B在x轴的正半轴上,∠ABO=90°,点A的坐标为,将△ABO绕点O逆时针旋转,使点B的对应点B′落在边OA上,则A′的坐标为( )
A. B. C. D.
二、填空题
1、如图,在等腰梯形中,,,直角三角板含角的顶点在边上移动,一直角边始终经过点,斜边与所在的直线交于点.若为等腰三角形,则的长等于______.
2、在Rt△ABC中,∠C=90°,tanA=,则sinB的值为_____.
3、在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部处测得办公楼底部处的俯角是,从综合楼底部处测得办公楼顶部处的仰角恰好是,综合楼的高为24米,则办公楼的高度约是______米.(结果精确到0.1,参考数据:,,.)
4、如图,点P,A,B,C在同一平面内,点A,B,C在同一直线上,且PC⊥AC,在点A处测得点P在北偏东60°方向上,在点B处测得点P在北偏东30°方向上,若AP=12千米,则A,B两点的距离为 ___千米.
5、如图,一架水平飞行的无人机在A处测得正前方河岸边C处的俯角为α,,无人机沿水平线AF方向继续飞行80米至B处时,被河对岸D处的小明测得其仰角为.无人机距地面的垂直高度用AM表示,点M,C,D在同一条直线上,其中米,则河流的宽度CD为______.
6、小明用一块含有角()的直角三角尺测量校园内某棵树的高度,示意图如图所示.若小明的眼睛与地面之间的垂直高度为,小明与树之间的水平距离为,则这棵树的高度约为______.(结果精确到,参考数据:)
三、解答题
1、如图,-楼房AB后有一-假山CD,CD的坡度为,测得B与C的距离为24米,山坡坡面上E点处有一休息亭,与山脚C的距离米,小丽从楼房房顶A处测得E的俯角为45°.
(1)求点E到水平地面的距离;
(2)求楼房AB的高.
2、如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面,坡角.在阳光下,小明观察到在地面上的影长为,在坡面上的影长为.同一时刻,小明测得直立于地面长60cm的木杆的影长为90cm(其影子完全落在地面上).求立柱AB的高度.
3、如图,小华利用标杆和等腰直角三角尺测量楼高,他先在E处竖立一根高1.5米的标杆DE,发现地面上的点A、标杆顶端D与楼顶B在一条直线上,测得米;然后他站在F处利用等腰直角三角形测得视线GB与水平面的夹角,小华的眼睛到地面的距离米,米.已知点F、A、E、C在同一直线上,,,.请根据以上所测数据,计算楼高BC.
4、湖中小岛上码头C处一名游客突发疾病,需要救援.位于湖面B点处的快艇和湖岸A处的救援船接到通知后立刻同时出发前往救援.计划由快艇赶到码头C接该游客,再沿方向行驶,与救援船相遇后将该游客转运到救援船上.已知C在A的北偏东30°方向上,B在A的北偏东60°方向上,且B在C的正南方向900米处.
(1)求湖岸A与码头C的距离(结果精确到1米,参考数据:);
(2)救援船的平均速度为150米/分,快艇的平均速度为400米/分,在接到通知后,快艇能否在5分钟内将该游客送上救援船?请说明理由.(接送游客上下船的时间忽略不计)
5、如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边AB、BC于点D、E,连结AE.
(1)如果∠B=25°,求∠CAE的度数;
(2)如果CE=2,,求的值.
6、如图,株洲市炎陵县某中学在实施“五项管理”中,将学校的“五项管理”做成宣传牌(CD),放置在教学楼A栋的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿芙蓉小学围墙边坡AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:3,AB=2m,AE=8m.
(1)求点B距水平面AE的高度BH.
(2)求宣传牌CD的高度.(结果精确到0.1米.参考数据:≈1.414 ,≈1.732 )
