人教版七年级数学 下册 第八章 8.3 实际问题与二元一次方程组 课件(共30张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第八章 8.3 实际问题与二元一次方程组 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-12 14:29:39 | ||
图片预览










文档简介
(共30张PPT)
用方程法解决实际问题的步骤:
(1)______ (2)______
(3)______ (4)___ __
(5)______ (6)______
审题
设未知数
列方程
解方程
检验
答
知识回顾
星期天,我们一家6个人去东郊公园看了灯光秀,买门票花了100元。
哦,那你们家去了几个大人?几个小孩呢?
聪明的同学们,你能帮他算算吗?
你太不聪明了,自已不会算吗?成人票每人20元,小孩票每人10元啊!
情境导入
数学
七年级 下册
8.3 实际问题与二元一次方程组
第八章 二元一次方程组
目标导航
1.能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.(重点)
2.学会利用二元一次方程组解决几何、行程问题.(重点、难点)
问题引入
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李
大叔估计的准确吗?
目标导学一:列方程组解决实际问题
问1:题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;每头小牛1天需用的饲料.
问2:题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用饲料为xkg和ykg.
互动探究
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
30x+15y=675,
42x+20y=940.
解这个方程组,得:
x=20,
y=5.
这就是说,平均每头大牛1天约需饲料20kg,每头小牛1天约需饲料5kg.饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
互动探究
解题小结:用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解
出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,
然后作答.
总结归纳
数量关系
字母
2
代入消元
加减消元法
典例精析
例1 某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后出售,所获利润全部捐给山区困难孩子,每件文化衫的批发价和零售价如下表:
假设文化衫全部售出,共获利1860元,求黑白两种文化衫各有多少件.
批发价(元) 零售价(元)
黑色文化衫 10 25
白色文化衫 8 20
解:设黑色文化衫有x件,白色文化衫有y件,
依题意得
解得
答:黑色文化衫有60件,白色文化衫有80件.
典例精析
长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?
解:设应取2米的x段,1米的y段,则
答:小明估计不准确。2米的应取8段,1米的应取2段。
解得:
依题意得
小试牛刀
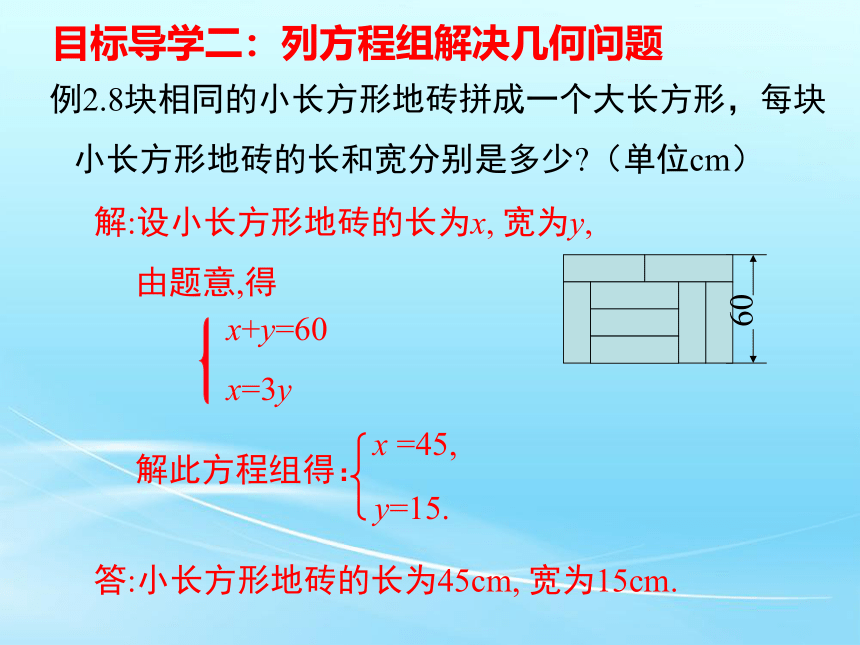
例2.8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (单位cm)
60
x+y=60
x=3y
解:设小长方形地砖的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
目标导学二:列方程组解决几何问题
例3.据统计资料,甲、乙两种作物的单位面积产量的比是1:2. 现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
B
A
C
D
典例精析
A
D
C
B
E
F
甲
乙
x
y
解:过点E作EF⊥CD,交CD于点F.设AE=xm,BE=ym.
根据题意,列方程组
解这个方程组,得
答:过长方形土地的长边上离一端120m处,作这条边的垂线,把这块土地分为两块长方形土地.较大的一块土地种甲种作物,较小的一块种乙种作物.
x+y=200,
100x:(2×100y)=3:4.
x=120,
y=80.
典例精析
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄
顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
目标导学三:列方程组解决行程问题
例3
解:设悟空行走速度是每分钟x里, 风速是每分钟y里,则
4(x-y)=600
x=200 y=50
答:风速是每分钟50里。
4(x+y)=1000
解得:
依题意得
例4 某果品公司通往甲、乙两地都要经过水路和陆路,这家公司从甲地购进一批水果运回公司加工成果汁再销往乙地,已知水路、陆路的运价及里程数如下表,若这两次运输支出水路运费10000元,陆路运费8000元,问该公司运进水果和运出果汁各多少吨?
水路 陆路
从甲地到公司(千米) 20 30
从公司到乙地(千米) 10 40
运价:元/(吨·千米) 2 1
目标导学四:列方程组解决其他问题
分析:设运进水果x吨,运出果汁y吨
水路运费 陆路运费
从甲地到公司
从公司到乙地
2x·20
30x
2y·10
40y
解:设该公司运进水果x吨,运出果汁y吨,则
2x·20+2y·10=10000
30x+40y=8000
解得
x=240
y=20
答:该公司运进水果240吨,运出果汁20吨.
例5.某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元,若制成奶片销售,每吨可获利润2000元.该厂生产能力如下:每天可加工3吨酸奶或1吨奶片,受人员和季节的限制,两种方式不能同时进行.受季节的限制,这批牛奶必须在4天内加工并销售完毕,为此该厂制定了两套方案:
方案一:尽可能多的制成奶片,其余直接销售现牛奶
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成
(1)你认为哪种方案获利最多,为什么 (2)本题解出之后,你还能提出哪些问题
典例精析
其余5吨直接销售,获利500×5=2500(元) ∴共获利:8000+2500=10500(元)
方案二:设生产奶片用x天,生 产酸奶用y天
另:设x吨鲜奶制成奶片,y吨鲜奶制成酸奶
x+y=4
x+3y=9
x+y=9
x=1.5
y=2.5
x=1.5
y=7.5
方案一:生产奶片4天,共制成4吨奶片,获利 2000×4=8000
1.5×1×2000+2.5×3×1200
=12000
∴共获利:
1.5×2000+7.5×1200
=3000+9000=12000
∴共获利:
两种酒精,甲种含水15%,乙种含水5%,现在要配成含水12%的酒精500克.每种酒精各需多少克
解此方程组,得
x=350
y=150
依题意,得
x+y=500
15% x+5%y=500×12%
即
x+y=500
3x+y=1200
答:甲种酒精取350克,乙种酒精取150克.
解:设甲种酒精取x克,乙种酒精取y克.
酒精重量
含水量
甲 种
乙 种
甲 种
乙 种
熔化前
熔化后
x克
y克
15%·x
5%·y
500克
500×12%
小试牛刀
实际问题
数学问题
(二元一次方程组)
解方程组
数学问题的解
(二元一次方程组的解)
双检验
实际问题
的答案
代入法
加减法
(消元)
设未知数、列方程组
课堂小结
1.食堂有一批粮食,若每天用去140千克,按预计天数计算就少50千克;若每天用去120千克,那么到期后还可剩余70千克.估计食堂现有粮食700~800千克,可供应时间为一周. 通过计算检验估计是否正确?
解:设预计使用天数为x天,共有粮食y千克,根据题意,得
解方程组,得
答:共有粮食790千克,可供应6天. 对粮食存量估计正确,对可供应时间估计偏高.
检测目标
2.篮球比赛中,每胜一场得2分,负一场得1分,某班篮球队参加了8场比赛中共得积分14分,若设某把篮球队胜了x场,负了y场,
则可列方程组为: .
检测目标
3.某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售。该公司的加工能力是:每天可以精加工6吨或粗加工16吨。现计划用15天完成加工任务,该公司应安排几天精加工,几天粗加工?
解:设该公司应安排x天精加工,y天粗加工,
x+y=15
6x+16y=140
解 得:
x=10
y=5
答:该公司应安排10天精加工,5天粗加工。
依题意得
若未说明,下列3种方案,①全部粗加工;②全部精加工;③部分精加工,剩下的粗加工。你选择那种?
检测目标
4.小敏做拼图游戏时发现:8个一样大小的小长方形恰好可以拼成一个大的长方形,如图①所示.小颖看见了,也来试一试,结果拼成了如图②所示的正方形,不过中间留下了一个边长为2cm的小正方形空白,你能算出每个小长方形的长和宽各为多少吗?
检测目标
解:设每个小长方形的长为xcm,宽为ycm.
由题意,得
解得
答:每个小长方形的长为10cm,宽为6cm.
检测目标
作 业 :
1.完成同步练习题
2.背诵知识点
谈谈你的收获吧
谢谢大家的努力
用方程法解决实际问题的步骤:
(1)______ (2)______
(3)______ (4)___ __
(5)______ (6)______
审题
设未知数
列方程
解方程
检验
答
知识回顾
星期天,我们一家6个人去东郊公园看了灯光秀,买门票花了100元。
哦,那你们家去了几个大人?几个小孩呢?
聪明的同学们,你能帮他算算吗?
你太不聪明了,自已不会算吗?成人票每人20元,小孩票每人10元啊!
情境导入
数学
七年级 下册
8.3 实际问题与二元一次方程组
第八章 二元一次方程组
目标导航
1.能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.(重点)
2.学会利用二元一次方程组解决几何、行程问题.(重点、难点)
问题引入
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李
大叔估计的准确吗?
目标导学一:列方程组解决实际问题
问1:题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;每头小牛1天需用的饲料.
问2:题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用饲料为xkg和ykg.
互动探究
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
30x+15y=675,
42x+20y=940.
解这个方程组,得:
x=20,
y=5.
这就是说,平均每头大牛1天约需饲料20kg,每头小牛1天约需饲料5kg.饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
互动探究
解题小结:用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解
出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,
然后作答.
总结归纳
数量关系
字母
2
代入消元
加减消元法
典例精析
例1 某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后出售,所获利润全部捐给山区困难孩子,每件文化衫的批发价和零售价如下表:
假设文化衫全部售出,共获利1860元,求黑白两种文化衫各有多少件.
批发价(元) 零售价(元)
黑色文化衫 10 25
白色文化衫 8 20
解:设黑色文化衫有x件,白色文化衫有y件,
依题意得
解得
答:黑色文化衫有60件,白色文化衫有80件.
典例精析
长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?
解:设应取2米的x段,1米的y段,则
答:小明估计不准确。2米的应取8段,1米的应取2段。
解得:
依题意得
小试牛刀
例2.8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (单位cm)
60
x+y=60
x=3y
解:设小长方形地砖的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
目标导学二:列方程组解决几何问题
例3.据统计资料,甲、乙两种作物的单位面积产量的比是1:2. 现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
B
A
C
D
典例精析
A
D
C
B
E
F
甲
乙
x
y
解:过点E作EF⊥CD,交CD于点F.设AE=xm,BE=ym.
根据题意,列方程组
解这个方程组,得
答:过长方形土地的长边上离一端120m处,作这条边的垂线,把这块土地分为两块长方形土地.较大的一块土地种甲种作物,较小的一块种乙种作物.
x+y=200,
100x:(2×100y)=3:4.
x=120,
y=80.
典例精析
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄
顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
目标导学三:列方程组解决行程问题
例3
解:设悟空行走速度是每分钟x里, 风速是每分钟y里,则
4(x-y)=600
x=200 y=50
答:风速是每分钟50里。
4(x+y)=1000
解得:
依题意得
例4 某果品公司通往甲、乙两地都要经过水路和陆路,这家公司从甲地购进一批水果运回公司加工成果汁再销往乙地,已知水路、陆路的运价及里程数如下表,若这两次运输支出水路运费10000元,陆路运费8000元,问该公司运进水果和运出果汁各多少吨?
水路 陆路
从甲地到公司(千米) 20 30
从公司到乙地(千米) 10 40
运价:元/(吨·千米) 2 1
目标导学四:列方程组解决其他问题
分析:设运进水果x吨,运出果汁y吨
水路运费 陆路运费
从甲地到公司
从公司到乙地
2x·20
30x
2y·10
40y
解:设该公司运进水果x吨,运出果汁y吨,则
2x·20+2y·10=10000
30x+40y=8000
解得
x=240
y=20
答:该公司运进水果240吨,运出果汁20吨.
例5.某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元,若制成奶片销售,每吨可获利润2000元.该厂生产能力如下:每天可加工3吨酸奶或1吨奶片,受人员和季节的限制,两种方式不能同时进行.受季节的限制,这批牛奶必须在4天内加工并销售完毕,为此该厂制定了两套方案:
方案一:尽可能多的制成奶片,其余直接销售现牛奶
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成
(1)你认为哪种方案获利最多,为什么 (2)本题解出之后,你还能提出哪些问题
典例精析
其余5吨直接销售,获利500×5=2500(元) ∴共获利:8000+2500=10500(元)
方案二:设生产奶片用x天,生 产酸奶用y天
另:设x吨鲜奶制成奶片,y吨鲜奶制成酸奶
x+y=4
x+3y=9
x+y=9
x=1.5
y=2.5
x=1.5
y=7.5
方案一:生产奶片4天,共制成4吨奶片,获利 2000×4=8000
1.5×1×2000+2.5×3×1200
=12000
∴共获利:
1.5×2000+7.5×1200
=3000+9000=12000
∴共获利:
两种酒精,甲种含水15%,乙种含水5%,现在要配成含水12%的酒精500克.每种酒精各需多少克
解此方程组,得
x=350
y=150
依题意,得
x+y=500
15% x+5%y=500×12%
即
x+y=500
3x+y=1200
答:甲种酒精取350克,乙种酒精取150克.
解:设甲种酒精取x克,乙种酒精取y克.
酒精重量
含水量
甲 种
乙 种
甲 种
乙 种
熔化前
熔化后
x克
y克
15%·x
5%·y
500克
500×12%
小试牛刀
实际问题
数学问题
(二元一次方程组)
解方程组
数学问题的解
(二元一次方程组的解)
双检验
实际问题
的答案
代入法
加减法
(消元)
设未知数、列方程组
课堂小结
1.食堂有一批粮食,若每天用去140千克,按预计天数计算就少50千克;若每天用去120千克,那么到期后还可剩余70千克.估计食堂现有粮食700~800千克,可供应时间为一周. 通过计算检验估计是否正确?
解:设预计使用天数为x天,共有粮食y千克,根据题意,得
解方程组,得
答:共有粮食790千克,可供应6天. 对粮食存量估计正确,对可供应时间估计偏高.
检测目标
2.篮球比赛中,每胜一场得2分,负一场得1分,某班篮球队参加了8场比赛中共得积分14分,若设某把篮球队胜了x场,负了y场,
则可列方程组为: .
检测目标
3.某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售。该公司的加工能力是:每天可以精加工6吨或粗加工16吨。现计划用15天完成加工任务,该公司应安排几天精加工,几天粗加工?
解:设该公司应安排x天精加工,y天粗加工,
x+y=15
6x+16y=140
解 得:
x=10
y=5
答:该公司应安排10天精加工,5天粗加工。
依题意得
若未说明,下列3种方案,①全部粗加工;②全部精加工;③部分精加工,剩下的粗加工。你选择那种?
检测目标
4.小敏做拼图游戏时发现:8个一样大小的小长方形恰好可以拼成一个大的长方形,如图①所示.小颖看见了,也来试一试,结果拼成了如图②所示的正方形,不过中间留下了一个边长为2cm的小正方形空白,你能算出每个小长方形的长和宽各为多少吗?
检测目标
解:设每个小长方形的长为xcm,宽为ycm.
由题意,得
解得
答:每个小长方形的长为10cm,宽为6cm.
检测目标
作 业 :
1.完成同步练习题
2.背诵知识点
谈谈你的收获吧
谢谢大家的努力
