人教版七年级数学 下册 第八章 8.4 三元一次方程组的解法 课件(共31张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第八章 8.4 三元一次方程组的解法 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-12 14:30:58 | ||
图片预览










文档简介
(共31张PPT)
我们学过哪几种解二元一次方程组的方法?
代入消元法,加减消元法。
解二元一次方程组的思想是什么?
转化思想、消元思想、方程(组)思想.
知识回顾
纸币问题
小明手头有12张面额分别是1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元的纸币各多少张?
提出问题:1.题目中有几个条件?
2.问题中有几个未知量?
3.根据等量关系你能列出方程组吗?
提出问题
分析: ①题目中有___个未知数,含有____个相等关系?
②设1元、2元、5元纸币分别为x张、y张、z张,根据题意的等量关系,可列得到出____个方程:
x+y+z=__
x+2y+5z=__
x=__y
③这个方程组含有___个相同的未知数,每个方程中含未知数的项的次数都是___,并且一共有_ _个方程,这样的方程组叫做__________方程组.
我们如何解这三元一次方程组?
x+y+z=12 ①
x+2y+5z=22 ②
x=4y ③
3
3
3
12
22
4
3
1
3
三元一次
提出问题
数学
七年级 下册
8.4 三元一次方程组的解法
第八章 二元一次方程组
学习目标
1.理解三元一次方程组的定义;
2.掌握三元一次方程组的解法;
3.会解简单的三元一次方程组应用题。
合作探究
已知小乐、小翼、小优三个同学年龄之和为 26 岁,小乐年龄的 2 倍与小优的年龄之和比小翼大 18 岁,小乐比小翼大 1 岁,求三个同学的年龄.
问题1:题中有未知量?你能找出哪些等量关系?
目标导学一:三元一次方程(组)的概念
未知量:
小乐的年龄
小翼的年龄
小优的年龄
每一个未知量都用一个字母表示
x 岁
y 岁
z 岁
三个未知数(元)
等量关系:
(1)小乐的年龄 + 小翼的年龄 + 小优的年龄 = 26
(2)小乐的年龄 - 1 = 小翼的年龄
(3) 2×小乐的年龄+小优的年龄=小翼的年龄+18
用方程表示等量关系.
x + y + z = 26
①
x - 1 = y
②
2x + z = y + 18
③
问题2:观察列出的三个方程,你有什么发现?
x + y + z = 26
①
x - 1 = y
②
2x + z = y + 18
③
二元一次方程
三元一次方程
含两个未知数
未知数的次数都是 1
含三个未知数
未知数的次数都是 1
三元一次方程
知识归纳
这个方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
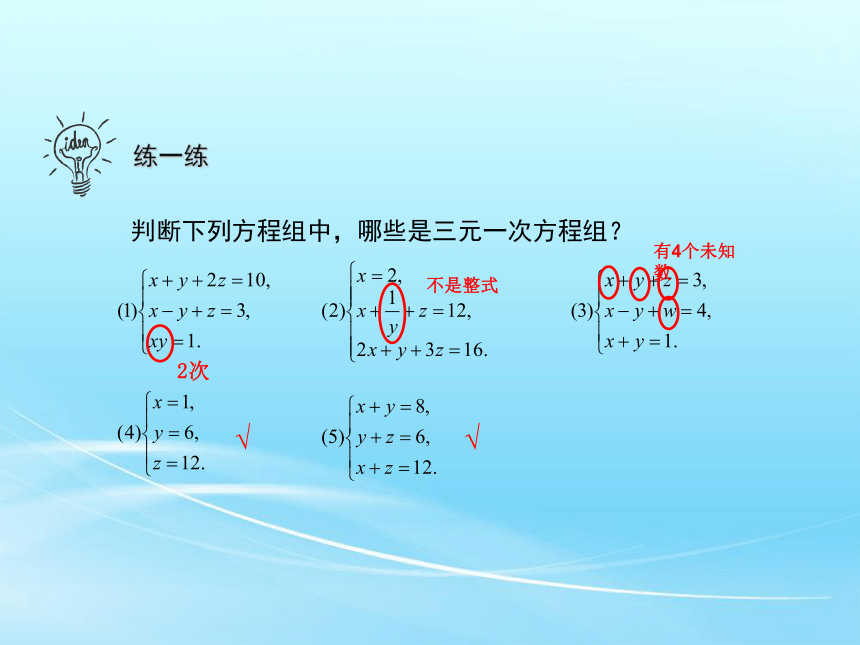
练一练
判断下列方程组中,哪些是三元一次方程组?
√
2次
不是整式
有4个未知数
√
类似二元一次方程组的解,三元一次方程组中各个方程的公共解,叫做这个三元一次方程组的解.
怎样解三元一次方程组呢?
能不能像以前一样“消元”,把“三元”化成“二元”呢?
目标导学二:三元一次方程组的解
例1:解方程组:
解:把(3)分别代入(1)、(2)得:
(4)
(5)
把y=____代入(3),
得x=____
∴三元一次方程组的解为
解这个方程组,得
4y+y+z=12
4y+2y+5z=22
5y+z=12
6y+5z=22
2
2
2
8
2
2
8
把方程(4)、(5)组成方程组
精典例题
仿照例1解三元一次方程组:
解:把(1)分别代入(2)、(3)得:
(4)
(5)
把y=____代入(3),
得x=____
∴三元一次方程组的解为
解这个方程组,得
y+z=0
2y+z=-1
y+z=0
2y+z=-1
-1
1
-1
2
-1
1
2
把方程(4)、(5)组成方程组
精典例题
1.变形:将三元一次方程组通过消元变为为二元一次方程组;
2.求解:解二元一次方程组;
3.回代:将求得的未知数的值代入原方程组的一个适当的方程中,得到一个一元一次方程;
4.求解:解一元一次方程,求出第三个未知数;
5.写解:用大括号将所求的的三个未知数的值联立起来,即得原方程组的解.
解三元一次方程组的基本步骤:
步骤归纳
总结
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
解三元一次方程的基本思路:
x的值 -1 2 5
y的值 0 3 60
分析
例2 在等式 中,当 时, ;当 时,
;当 时, .求 的值?
4a+2b+c
25a+5b+c
4a+2b+c=3
25a+5b+c=60
精典例题
解:根据题意,得三元一次方程组
①②③
解这个方程组,得
④与⑤组成方程组
②-①,得
④
③-①,得
⑤
因此
把 代入①中,得
即 的值分别为3、-2、-5.
例3 在等式 中,当 时, ;当 时,
;当 时, .求 的值?
精典例题
例4. 阅读材料:
已知方程组 求 x + y + z 的值.
解法二:
将原方程组整理得
②-①,得 x + 2y = 3.③
将③代入①,得 x + y + z = 5.
②-①,得 x = 3 - 2y.③
将③代入①,得
2(3 - 2y) + z = 8 - 3y.
z = 2 + y 所以 x + y + z =
(3 - 2y) + y + (2 + y) = 5
解法一:有原方程组,得
精典例题
若|a-b-1|+(b-2a+c)2+|2c-b|=0,求a,b,c的值.
解:因为三个非负数的和等于0,所以每个非负数都为0.
可得方程组
解得
小试牛刀
例5.幼儿营养标准中要求每一个幼儿每天所需的营养量中应包含35单位的铁、70单位的钙和35单位的维生素.现有一批营养师根据上面的标准给幼儿园小朋友们配餐,其中包含A、B、C三种食物,下表给出的是每份(50g)食物A、B、C分别所含的铁、钙和维生素的量(单位)
食物 铁 钙 维生素
A 5 20 5
B 5 10 15
C 10 10 5
目标导学三:三元一次方程组的应用
例5.一个三位数,个位、百位上的数的和等于十位上的数,百位上的数的7倍比个位、十位上的数的和大2,且个位、十位、百位上的数的和为14.求这个三位数.
分析
个位、百位上的数的和等于十位上的数
百位上的数的7倍比个位、十位上的数的和大2
个位、十位、百位上的数的和为14
三元一次方程组
三元一次方程及三元一次方程组的概念
三元一次方程组的解法
①解三元一次方程组的基本方法是代入法和加减法,其中加减法比较常用.
②解三元一次方程组的基本思想是消元,关键也是消元,我们一定要根据方程组的特点,选准消元对象,定好消元方案.
③解完后要代入原方程组的三个方程中进行检验.
课堂小结
1.已知三元一次方程组 ,则x+y+z=( )
A.20 B.30 C.35 D.70
C
检测目标
2. 下列方程组不是三元一次方程组的是 ( )
C
检测目标
3.若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为( )
A.2 B.3 C.4 D.5
D
检测目标
4.解三元一次方程组
①②③
解:①+②×2,得
④
②×3-③,得
⑤
④与⑤组成方程组
解这个方程组,得
因此,这个三元一次方程组的解为
把 代入①中,得
检测目标
5.甲、乙、丙三个数的和是35,甲数的2倍比乙数大5,乙数的 等于丙数的 ,求这三个数.
答:甲、乙、丙三个数分别是10,15,10 .
解:设甲、乙、丙三个数分别是x,y,z .
由题意,得
解得
检测目标
作 业 :
1.完成同步练习题
2.背诵知识点
谈谈你的收获吧
谢谢大家的努力
我们学过哪几种解二元一次方程组的方法?
代入消元法,加减消元法。
解二元一次方程组的思想是什么?
转化思想、消元思想、方程(组)思想.
知识回顾
纸币问题
小明手头有12张面额分别是1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元的纸币各多少张?
提出问题:1.题目中有几个条件?
2.问题中有几个未知量?
3.根据等量关系你能列出方程组吗?
提出问题
分析: ①题目中有___个未知数,含有____个相等关系?
②设1元、2元、5元纸币分别为x张、y张、z张,根据题意的等量关系,可列得到出____个方程:
x+y+z=__
x+2y+5z=__
x=__y
③这个方程组含有___个相同的未知数,每个方程中含未知数的项的次数都是___,并且一共有_ _个方程,这样的方程组叫做__________方程组.
我们如何解这三元一次方程组?
x+y+z=12 ①
x+2y+5z=22 ②
x=4y ③
3
3
3
12
22
4
3
1
3
三元一次
提出问题
数学
七年级 下册
8.4 三元一次方程组的解法
第八章 二元一次方程组
学习目标
1.理解三元一次方程组的定义;
2.掌握三元一次方程组的解法;
3.会解简单的三元一次方程组应用题。
合作探究
已知小乐、小翼、小优三个同学年龄之和为 26 岁,小乐年龄的 2 倍与小优的年龄之和比小翼大 18 岁,小乐比小翼大 1 岁,求三个同学的年龄.
问题1:题中有未知量?你能找出哪些等量关系?
目标导学一:三元一次方程(组)的概念
未知量:
小乐的年龄
小翼的年龄
小优的年龄
每一个未知量都用一个字母表示
x 岁
y 岁
z 岁
三个未知数(元)
等量关系:
(1)小乐的年龄 + 小翼的年龄 + 小优的年龄 = 26
(2)小乐的年龄 - 1 = 小翼的年龄
(3) 2×小乐的年龄+小优的年龄=小翼的年龄+18
用方程表示等量关系.
x + y + z = 26
①
x - 1 = y
②
2x + z = y + 18
③
问题2:观察列出的三个方程,你有什么发现?
x + y + z = 26
①
x - 1 = y
②
2x + z = y + 18
③
二元一次方程
三元一次方程
含两个未知数
未知数的次数都是 1
含三个未知数
未知数的次数都是 1
三元一次方程
知识归纳
这个方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
练一练
判断下列方程组中,哪些是三元一次方程组?
√
2次
不是整式
有4个未知数
√
类似二元一次方程组的解,三元一次方程组中各个方程的公共解,叫做这个三元一次方程组的解.
怎样解三元一次方程组呢?
能不能像以前一样“消元”,把“三元”化成“二元”呢?
目标导学二:三元一次方程组的解
例1:解方程组:
解:把(3)分别代入(1)、(2)得:
(4)
(5)
把y=____代入(3),
得x=____
∴三元一次方程组的解为
解这个方程组,得
4y+y+z=12
4y+2y+5z=22
5y+z=12
6y+5z=22
2
2
2
8
2
2
8
把方程(4)、(5)组成方程组
精典例题
仿照例1解三元一次方程组:
解:把(1)分别代入(2)、(3)得:
(4)
(5)
把y=____代入(3),
得x=____
∴三元一次方程组的解为
解这个方程组,得
y+z=0
2y+z=-1
y+z=0
2y+z=-1
-1
1
-1
2
-1
1
2
把方程(4)、(5)组成方程组
精典例题
1.变形:将三元一次方程组通过消元变为为二元一次方程组;
2.求解:解二元一次方程组;
3.回代:将求得的未知数的值代入原方程组的一个适当的方程中,得到一个一元一次方程;
4.求解:解一元一次方程,求出第三个未知数;
5.写解:用大括号将所求的的三个未知数的值联立起来,即得原方程组的解.
解三元一次方程组的基本步骤:
步骤归纳
总结
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
解三元一次方程的基本思路:
x的值 -1 2 5
y的值 0 3 60
分析
例2 在等式 中,当 时, ;当 时,
;当 时, .求 的值?
4a+2b+c
25a+5b+c
4a+2b+c=3
25a+5b+c=60
精典例题
解:根据题意,得三元一次方程组
①②③
解这个方程组,得
④与⑤组成方程组
②-①,得
④
③-①,得
⑤
因此
把 代入①中,得
即 的值分别为3、-2、-5.
例3 在等式 中,当 时, ;当 时,
;当 时, .求 的值?
精典例题
例4. 阅读材料:
已知方程组 求 x + y + z 的值.
解法二:
将原方程组整理得
②-①,得 x + 2y = 3.③
将③代入①,得 x + y + z = 5.
②-①,得 x = 3 - 2y.③
将③代入①,得
2(3 - 2y) + z = 8 - 3y.
z = 2 + y 所以 x + y + z =
(3 - 2y) + y + (2 + y) = 5
解法一:有原方程组,得
精典例题
若|a-b-1|+(b-2a+c)2+|2c-b|=0,求a,b,c的值.
解:因为三个非负数的和等于0,所以每个非负数都为0.
可得方程组
解得
小试牛刀
例5.幼儿营养标准中要求每一个幼儿每天所需的营养量中应包含35单位的铁、70单位的钙和35单位的维生素.现有一批营养师根据上面的标准给幼儿园小朋友们配餐,其中包含A、B、C三种食物,下表给出的是每份(50g)食物A、B、C分别所含的铁、钙和维生素的量(单位)
食物 铁 钙 维生素
A 5 20 5
B 5 10 15
C 10 10 5
目标导学三:三元一次方程组的应用
例5.一个三位数,个位、百位上的数的和等于十位上的数,百位上的数的7倍比个位、十位上的数的和大2,且个位、十位、百位上的数的和为14.求这个三位数.
分析
个位、百位上的数的和等于十位上的数
百位上的数的7倍比个位、十位上的数的和大2
个位、十位、百位上的数的和为14
三元一次方程组
三元一次方程及三元一次方程组的概念
三元一次方程组的解法
①解三元一次方程组的基本方法是代入法和加减法,其中加减法比较常用.
②解三元一次方程组的基本思想是消元,关键也是消元,我们一定要根据方程组的特点,选准消元对象,定好消元方案.
③解完后要代入原方程组的三个方程中进行检验.
课堂小结
1.已知三元一次方程组 ,则x+y+z=( )
A.20 B.30 C.35 D.70
C
检测目标
2. 下列方程组不是三元一次方程组的是 ( )
C
检测目标
3.若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为( )
A.2 B.3 C.4 D.5
D
检测目标
4.解三元一次方程组
①②③
解:①+②×2,得
④
②×3-③,得
⑤
④与⑤组成方程组
解这个方程组,得
因此,这个三元一次方程组的解为
把 代入①中,得
检测目标
5.甲、乙、丙三个数的和是35,甲数的2倍比乙数大5,乙数的 等于丙数的 ,求这三个数.
答:甲、乙、丙三个数分别是10,15,10 .
解:设甲、乙、丙三个数分别是x,y,z .
由题意,得
解得
检测目标
作 业 :
1.完成同步练习题
2.背诵知识点
谈谈你的收获吧
谢谢大家的努力
