2022-2023学年苏教版(2019)必修二第十四章 统计 单元测试卷(含解析)
文档属性
| 名称 | 2022-2023学年苏教版(2019)必修二第十四章 统计 单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 424.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 22:44:48 | ||
图片预览



文档简介
苏教版(2019)必修二第十四章 统计 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、2021年某省高考体育百米测试中,成绩全部介于12秒与18秒之间,抽取其中100个样本,将测试结果按如下方式分成六组:第一组,第二组,…,第六组,得到如下的频率分布直方图.则该100名考生的成绩的平均数和中位数(保留一位小数)分别是( )
A.15.2 15.3 B.15.1 15.4 C.15.1 15.3 D.15.2 15.3
2、为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
①样本数据落在区间的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③估计样本的中位数为480万元.
其中正确结论的个数为( )
A.0 B.1 C.2 D.3
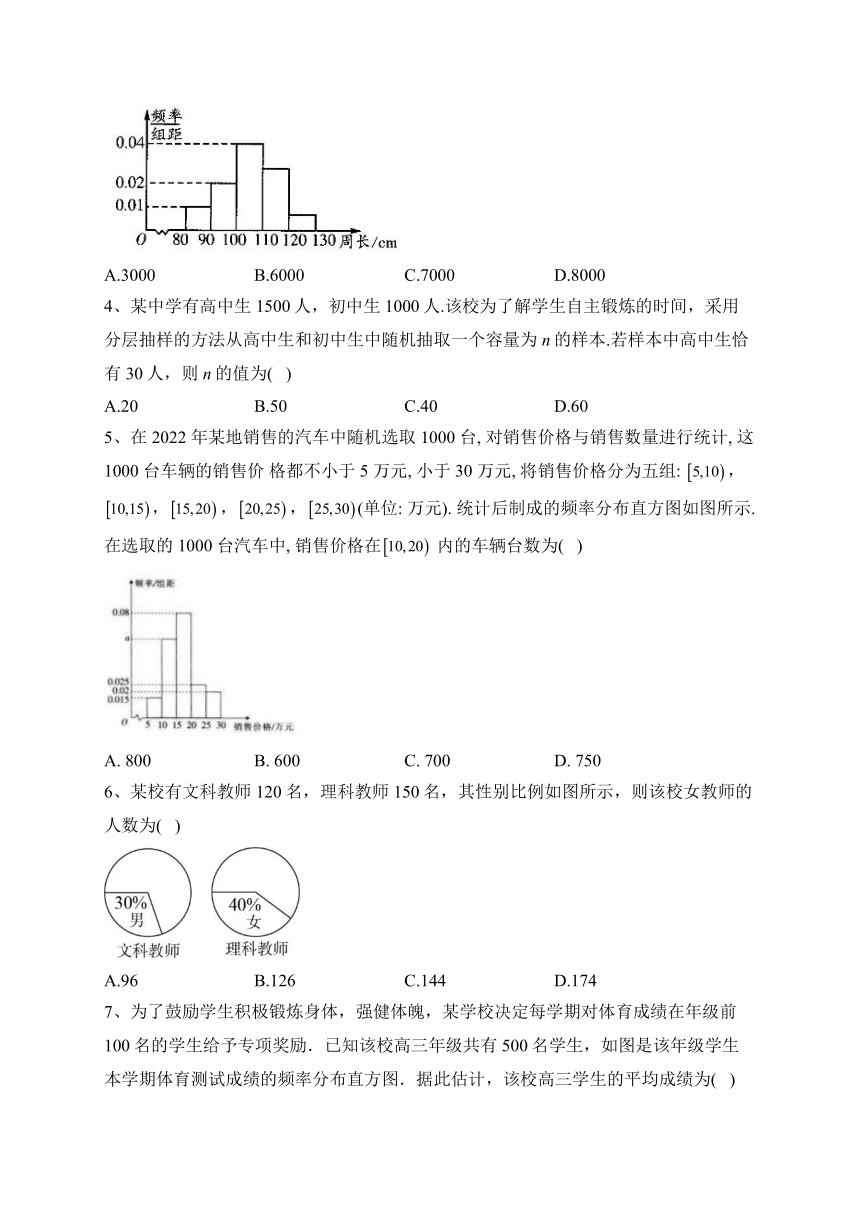
3、为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )
A.3000 B.6000 C.7000 D.8000
4、某中学有高中生1500人,初中生1000人.该校为了解学生自主锻炼的时间,采用分层抽样的方法从高中生和初中生中随机抽取一个容量为n的样本.若样本中高中生恰有30人,则n的值为( )
A.20 B.50 C.40 D.60
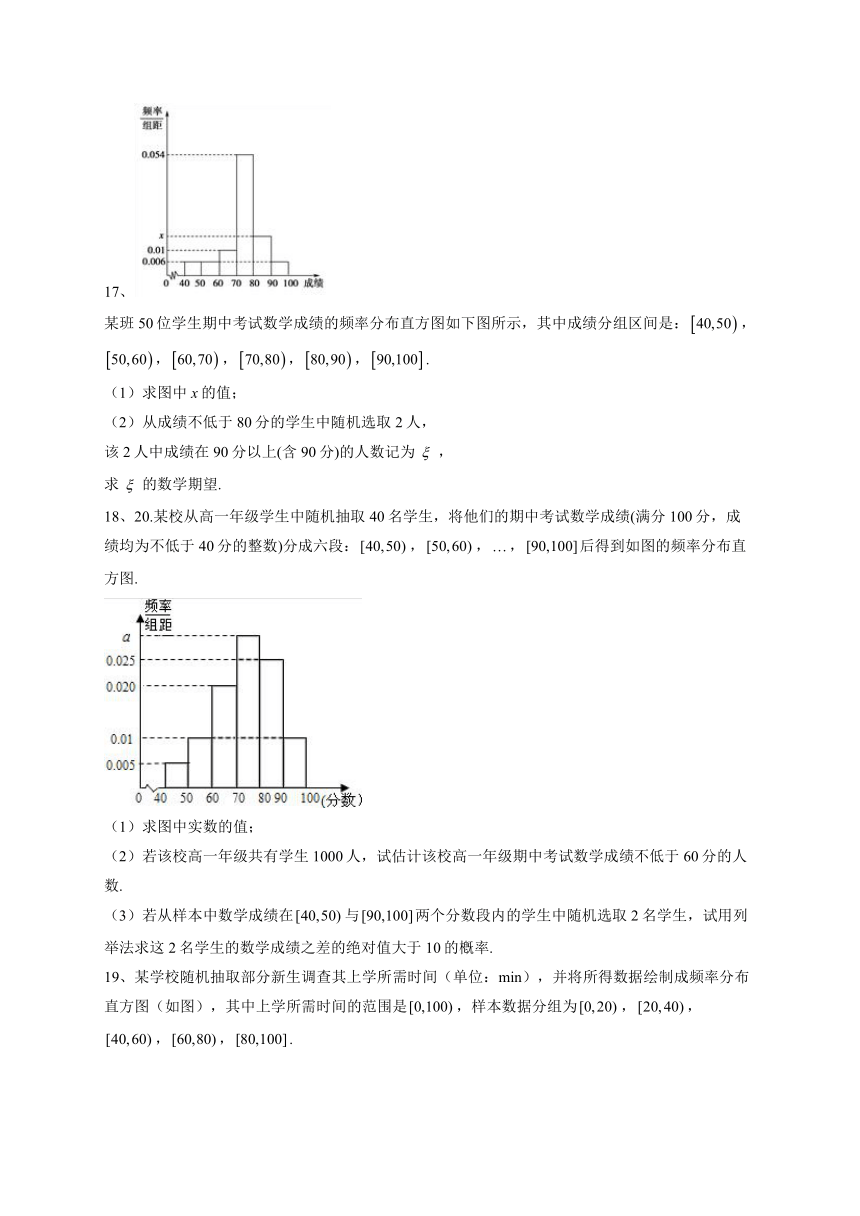
5、在 2022 年某地销售的汽车中随机选取 1000 台, 对销售价格与销售数量进行统计, 这 1000 台车辆的销售价 格都不小于 5 万元, 小于 30 万元, 将销售价格分为五组: ,,,,(单位: 万元). 统计后制成的频率分布直方图如图所示. 在选取的 1000 台汽车中, 销售价格在 内的车辆台数为( )
A. 800 B. 600 C. 700 D. 750
6、某校有文科教师120名,理科教师150名,其性别比例如图所示,则该校女教师的人数为( )
A.96 B.126 C.144 D.174
7、为了鼓励学生积极锻炼身体,强健体魄,某学校决定每学期对体育成绩在年级前100名的学生给予专项奖励.已知该校高三年级共有500名学生,如图是该年级学生本学期体育测试成绩的频率分布直方图.据此估计,该校高三学生的平均成绩为( )
A. 76 B. 71 C. 66 D. 63
8、2019年是中华人民共和国成立70周年,党中央、中央军委决定组织首都天安门阅兵,这是国家重大纪念日阅兵的制度化安排,参加受阅的徒步方队队员应身体健康、体型协调、反应敏捷.通常男性士兵的身高普遍在175cm至185cm之间,女性士兵的身高在163cm至175cm之间.某连队现有男性士兵120人,则根据男性士兵的身高得到的频率分布直方图如图.若a,bc,成等差数列,且,,则该连队男性士兵的身高符合国庆阅兵标准的人数为( )
A.48 B.54 C.60 D.66
9、5G手机是指使用第五代通信系统的智能手机,已经面市.相对4G手机,5G手机有更快的网络与通信,低时延,通过网络切片技术,拥有更精准的定位.这也导致了越来越多的人喜欢用手机上网.某学校为了调查该校学生使用手机上网的时间,随机抽取了200名学生,对他们每天使用手机上网的时间进行统计,并将得到的数据制成频率分布直方图,如图.其中使用手机上网的时间范围为,则下列叙述正确的是( )
A.a的值为0.06
B.上网时间在5~10min的频率为0.04
C.上网时间在15~20min的频数为30
D.上网时间的平均数为15min
10、一组数据1,-1,0,-1,1的方差和标准差分别是( )
A.0,0 B.0.8,0.64 C.1,1 D.,
二、填空题
11、为了了解某市不同年龄的居民对“执行垃圾分类”的看法,现从该市某小区随机抽查了年龄在10~70岁的100名住户,绘制出频率分布直方图如图所示,则所抽取的这100名住户的年龄的中位数为__________.
12、从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为__________.
分数 5 4 3 2 1
人数 20 10 30 30 10
13、已知甲同学6次数学期中考试的成绩如下表所示:
年级 高一(上) 高一(下) 高二(上) 高二(下) 高三(上) 高三(下)
成绩 120 115 135 98 130 125
则该同学6次数学考试成绩的中位数为___________.
14、一个志愿者组织有男,女成员84人.其中48名男成员中,45岁以上的有12人;36名女成员中,45岁以上的有18人.根据需要,按照年龄进行分层抽样,要从这个志愿者组织成员中抽取28人开展活动,则45岁以上的成员应抽取___________人.
15、某高中共有学生1000名,其中高一年级共有学生380人,高二年级男生有180人,如果在全校学生中抽取1名学生,抽到高二年级女生的概率为0.19,现采用分层抽样(按年级分层)在全校抽取100人,则应在高三年级中抽取的人数等于________.
16、某工厂为了解产品的生产情况,随机抽取了100个样本.若样本数据,,…,的方差为16,则数据,,…,的方差为_________.
三、解答题
17、
某班50位学生期中考试数学成绩的频率分布直方图如下图所示,其中成绩分组区间是:,,,,,.
(1)求图中x的值;
(2)从成绩不低于80分的学生中随机选取2人,
该2人中成绩在90分以上(含90分)的人数记为,
求的数学期望.
18、20.某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:,,,后得到如图的频率分布直方图.
(1)求图中实数的值;
(2)若该校高一年级共有学生1000人,试估计该校高一年级期中考试数学成绩不低于60分的人数.
(3)若从样本中数学成绩在与两个分数段内的学生中随机选取2名学生,试用列举法求这2名学生的数学成绩之差的绝对值大于10的槪率.
19、某学校随机抽取部分新生调查其上学所需时间(单位:min),并将所得数据绘制成频率分布直方图(如图),其中上学所需时间的范围是,样本数据分组为,,,,.
(1)求频率分布直方图中x的值;
(2)假设上学所需时间不少于1 h的学生可申请在学校住宿,若该学校有600名新生,请估计新生中有多少名学生可以申请住宿;
(3)由频率分布直方图估计该校新生上学所需时间的平均值.
20、为了对某课题进行研究,分别从A,B,C三所高校中用分层随机抽样法(样本量按比例分配)抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中).
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授数是高校A和C中抽取的教授总数的,求三所高校的教授的总人数.
参考答案
1、答案:C
解析:100名考生成绩的平均数.因为前三组频率直方图面积和为,前四组频率直方图面积和为,所以中位数位于第四组内,设中位数为a,则,解得,故选C.
2、答案:D
解析:由,得,
所以数据在区间的频率为,①正确;
数据在区间的频率为,②正确;
数据在区间的频率为0.3,数据在区间的频率为0.55,故估计中位数为,③正确.故选D.
3、答案:C
解析:底部周长小于110cm的频率为,所以底部周长小于110cm的株数大约是.故选C.
4、答案:B
解析:由题意,得,解得.故选B.
5、答案:C
解析:由频率分布直方图知, , 所以, 所以销售 价格在内的频率为, 故销售价格在内的车辆台数为
6、答案:C
解析:该校文科女教师的人数为,理科女教师的人数为,所以该校女教师的人数为144.故选C.
7、答案:B
解析:
该校高三学生的平均成绩的估计值为 71 分,
故选 : B.
8、答案:D
解析:a,b,c成等差数列,且,.则由频率分布直方图得,,解得,又,,,符合国庆阅兵标准的男性士兵的人数为.故选D.
9、答案:A
解析:由题图可得,所以,故A正确;上网时间在5~10min的频率为,故B错误;上网时间在15~20min的频率为,则频数为,故C错误;上网时间的平均数为(min),故D错误.故选A.
10、答案:D
解析:,
,
,故选D.
11、答案:
解析:设所抽取的这100名住户的年龄的中位数为m,
则有,
解得.
12、答案:
解析:因为,
所以
,所以.
13、答案:122.5
解析:将该同学6次数学考试成绩按照从小到大排列可得98,115,120,125,130,135,可得中位数为122.5,
故答案为:122.5.
14、答案:10
解析:依题意按照分层抽样45岁以上的成员应抽取(人);
故答案为:10
15、答案:25
解析:高二年的女生有高三学生有
高三年级中抽取的人数为人.
16、答案:64
解析:样本数据,,…,的方差为,则数据,,…,的方差为.
17、
(1)答案:0.018
解析:由,得.
(2)答案:
解析:由题意知道:不低于8的学生有12人,9以上的学生有3人
随机变量的可能取值有0,1,2
18、
(1)答案:
解析:由频率分布直方图,得:,解得.
(2)答案:850
解析:数学成绩不低于60分的概率为:,数学成绩不低于60分的人数为:(人).
(3)答案:
解析:数学成绩在的学生为40×0.05=2(人),数学成绩在的学生人数为(人),设数学成绩在的学生为A,B,数学成绩在的学生为a,b,c,d,从样本中数学成绩在与两个分数段内的学生中随机选取2名学生,基本事件有:,,,,,,,,,,,,,,
其中两名学生的数学成绩之差的绝对值大于10的情况有:
,,,,,,,,共8种,
这2名学生的数学成绩之差的绝对值大于10的槪率为.
19、答案:(1)0.0125(2)72(3)33.6 min
解析:(1)由频率分布直方图可得,解得.
(2)新生上学时间不少于1 h的频率为,
因为,
所以600名新生中约有72名学生可以申请住宿.
(3)由题可知.
故该校新生上学所需时间的平均值约为33.6 min.
20、答案:(1),
(2)三所高校的教授的总人数为180
解析:(1),A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,高校B中抽取2名教授,高校A中抽取1名教授,高校C中抽取3名教授,
,解得,.
(2)高校B中抽取的教授数是高校A和C中抽取的教授总数的,
,解得,
三所高校的教授的总人数为.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、2021年某省高考体育百米测试中,成绩全部介于12秒与18秒之间,抽取其中100个样本,将测试结果按如下方式分成六组:第一组,第二组,…,第六组,得到如下的频率分布直方图.则该100名考生的成绩的平均数和中位数(保留一位小数)分别是( )
A.15.2 15.3 B.15.1 15.4 C.15.1 15.3 D.15.2 15.3
2、为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
①样本数据落在区间的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③估计样本的中位数为480万元.
其中正确结论的个数为( )
A.0 B.1 C.2 D.3
3、为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )
A.3000 B.6000 C.7000 D.8000
4、某中学有高中生1500人,初中生1000人.该校为了解学生自主锻炼的时间,采用分层抽样的方法从高中生和初中生中随机抽取一个容量为n的样本.若样本中高中生恰有30人,则n的值为( )
A.20 B.50 C.40 D.60
5、在 2022 年某地销售的汽车中随机选取 1000 台, 对销售价格与销售数量进行统计, 这 1000 台车辆的销售价 格都不小于 5 万元, 小于 30 万元, 将销售价格分为五组: ,,,,(单位: 万元). 统计后制成的频率分布直方图如图所示. 在选取的 1000 台汽车中, 销售价格在 内的车辆台数为( )
A. 800 B. 600 C. 700 D. 750
6、某校有文科教师120名,理科教师150名,其性别比例如图所示,则该校女教师的人数为( )
A.96 B.126 C.144 D.174
7、为了鼓励学生积极锻炼身体,强健体魄,某学校决定每学期对体育成绩在年级前100名的学生给予专项奖励.已知该校高三年级共有500名学生,如图是该年级学生本学期体育测试成绩的频率分布直方图.据此估计,该校高三学生的平均成绩为( )
A. 76 B. 71 C. 66 D. 63
8、2019年是中华人民共和国成立70周年,党中央、中央军委决定组织首都天安门阅兵,这是国家重大纪念日阅兵的制度化安排,参加受阅的徒步方队队员应身体健康、体型协调、反应敏捷.通常男性士兵的身高普遍在175cm至185cm之间,女性士兵的身高在163cm至175cm之间.某连队现有男性士兵120人,则根据男性士兵的身高得到的频率分布直方图如图.若a,bc,成等差数列,且,,则该连队男性士兵的身高符合国庆阅兵标准的人数为( )
A.48 B.54 C.60 D.66
9、5G手机是指使用第五代通信系统的智能手机,已经面市.相对4G手机,5G手机有更快的网络与通信,低时延,通过网络切片技术,拥有更精准的定位.这也导致了越来越多的人喜欢用手机上网.某学校为了调查该校学生使用手机上网的时间,随机抽取了200名学生,对他们每天使用手机上网的时间进行统计,并将得到的数据制成频率分布直方图,如图.其中使用手机上网的时间范围为,则下列叙述正确的是( )
A.a的值为0.06
B.上网时间在5~10min的频率为0.04
C.上网时间在15~20min的频数为30
D.上网时间的平均数为15min
10、一组数据1,-1,0,-1,1的方差和标准差分别是( )
A.0,0 B.0.8,0.64 C.1,1 D.,
二、填空题
11、为了了解某市不同年龄的居民对“执行垃圾分类”的看法,现从该市某小区随机抽查了年龄在10~70岁的100名住户,绘制出频率分布直方图如图所示,则所抽取的这100名住户的年龄的中位数为__________.
12、从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为__________.
分数 5 4 3 2 1
人数 20 10 30 30 10
13、已知甲同学6次数学期中考试的成绩如下表所示:
年级 高一(上) 高一(下) 高二(上) 高二(下) 高三(上) 高三(下)
成绩 120 115 135 98 130 125
则该同学6次数学考试成绩的中位数为___________.
14、一个志愿者组织有男,女成员84人.其中48名男成员中,45岁以上的有12人;36名女成员中,45岁以上的有18人.根据需要,按照年龄进行分层抽样,要从这个志愿者组织成员中抽取28人开展活动,则45岁以上的成员应抽取___________人.
15、某高中共有学生1000名,其中高一年级共有学生380人,高二年级男生有180人,如果在全校学生中抽取1名学生,抽到高二年级女生的概率为0.19,现采用分层抽样(按年级分层)在全校抽取100人,则应在高三年级中抽取的人数等于________.
16、某工厂为了解产品的生产情况,随机抽取了100个样本.若样本数据,,…,的方差为16,则数据,,…,的方差为_________.
三、解答题
17、
某班50位学生期中考试数学成绩的频率分布直方图如下图所示,其中成绩分组区间是:,,,,,.
(1)求图中x的值;
(2)从成绩不低于80分的学生中随机选取2人,
该2人中成绩在90分以上(含90分)的人数记为,
求的数学期望.
18、20.某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:,,,后得到如图的频率分布直方图.
(1)求图中实数的值;
(2)若该校高一年级共有学生1000人,试估计该校高一年级期中考试数学成绩不低于60分的人数.
(3)若从样本中数学成绩在与两个分数段内的学生中随机选取2名学生,试用列举法求这2名学生的数学成绩之差的绝对值大于10的槪率.
19、某学校随机抽取部分新生调查其上学所需时间(单位:min),并将所得数据绘制成频率分布直方图(如图),其中上学所需时间的范围是,样本数据分组为,,,,.
(1)求频率分布直方图中x的值;
(2)假设上学所需时间不少于1 h的学生可申请在学校住宿,若该学校有600名新生,请估计新生中有多少名学生可以申请住宿;
(3)由频率分布直方图估计该校新生上学所需时间的平均值.
20、为了对某课题进行研究,分别从A,B,C三所高校中用分层随机抽样法(样本量按比例分配)抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中).
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授数是高校A和C中抽取的教授总数的,求三所高校的教授的总人数.
参考答案
1、答案:C
解析:100名考生成绩的平均数.因为前三组频率直方图面积和为,前四组频率直方图面积和为,所以中位数位于第四组内,设中位数为a,则,解得,故选C.
2、答案:D
解析:由,得,
所以数据在区间的频率为,①正确;
数据在区间的频率为,②正确;
数据在区间的频率为0.3,数据在区间的频率为0.55,故估计中位数为,③正确.故选D.
3、答案:C
解析:底部周长小于110cm的频率为,所以底部周长小于110cm的株数大约是.故选C.
4、答案:B
解析:由题意,得,解得.故选B.
5、答案:C
解析:由频率分布直方图知, , 所以, 所以销售 价格在内的频率为, 故销售价格在内的车辆台数为
6、答案:C
解析:该校文科女教师的人数为,理科女教师的人数为,所以该校女教师的人数为144.故选C.
7、答案:B
解析:
该校高三学生的平均成绩的估计值为 71 分,
故选 : B.
8、答案:D
解析:a,b,c成等差数列,且,.则由频率分布直方图得,,解得,又,,,符合国庆阅兵标准的男性士兵的人数为.故选D.
9、答案:A
解析:由题图可得,所以,故A正确;上网时间在5~10min的频率为,故B错误;上网时间在15~20min的频率为,则频数为,故C错误;上网时间的平均数为(min),故D错误.故选A.
10、答案:D
解析:,
,
,故选D.
11、答案:
解析:设所抽取的这100名住户的年龄的中位数为m,
则有,
解得.
12、答案:
解析:因为,
所以
,所以.
13、答案:122.5
解析:将该同学6次数学考试成绩按照从小到大排列可得98,115,120,125,130,135,可得中位数为122.5,
故答案为:122.5.
14、答案:10
解析:依题意按照分层抽样45岁以上的成员应抽取(人);
故答案为:10
15、答案:25
解析:高二年的女生有高三学生有
高三年级中抽取的人数为人.
16、答案:64
解析:样本数据,,…,的方差为,则数据,,…,的方差为.
17、
(1)答案:0.018
解析:由,得.
(2)答案:
解析:由题意知道:不低于8的学生有12人,9以上的学生有3人
随机变量的可能取值有0,1,2
18、
(1)答案:
解析:由频率分布直方图,得:,解得.
(2)答案:850
解析:数学成绩不低于60分的概率为:,数学成绩不低于60分的人数为:(人).
(3)答案:
解析:数学成绩在的学生为40×0.05=2(人),数学成绩在的学生人数为(人),设数学成绩在的学生为A,B,数学成绩在的学生为a,b,c,d,从样本中数学成绩在与两个分数段内的学生中随机选取2名学生,基本事件有:,,,,,,,,,,,,,,
其中两名学生的数学成绩之差的绝对值大于10的情况有:
,,,,,,,,共8种,
这2名学生的数学成绩之差的绝对值大于10的槪率为.
19、答案:(1)0.0125(2)72(3)33.6 min
解析:(1)由频率分布直方图可得,解得.
(2)新生上学时间不少于1 h的频率为,
因为,
所以600名新生中约有72名学生可以申请住宿.
(3)由题可知.
故该校新生上学所需时间的平均值约为33.6 min.
20、答案:(1),
(2)三所高校的教授的总人数为180
解析:(1),A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,高校B中抽取2名教授,高校A中抽取1名教授,高校C中抽取3名教授,
,解得,.
(2)高校B中抽取的教授数是高校A和C中抽取的教授总数的,
,解得,
三所高校的教授的总人数为.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
