第十八章 平行四边形 单元检测 (无答案) 2022-2023学年人教版数学八年级下册
文档属性
| 名称 | 第十八章 平行四边形 单元检测 (无答案) 2022-2023学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-12 15:24:08 | ||
图片预览


文档简介
第十八章 平行四边形
班级______ 姓名_______ 学号_____
一、选择题
1. 如果平行四边形 的 ,那么另三个内角 ,, 分别是 ( )
A. ,, B. ,,
C. ,, D. ,,
2. 已知平行四边形 中,,则 ( )
A. B. C. D. 或
3. 在 中,, 于 , 为 的中点,,则 的长为( )
A. B. C. D.
4.如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则 ABCD的周长是( )
A.24 B.18 C.16 D.12
5.如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A.(6,3) B.(3,6) C.(0,6) D.(6,6)
6. 如图,公路 , 互相垂直,公路 的中点 与点 被湖隔开,若测得 的长为 ,则 , 两点间的距离为( )
A. B. C. D.
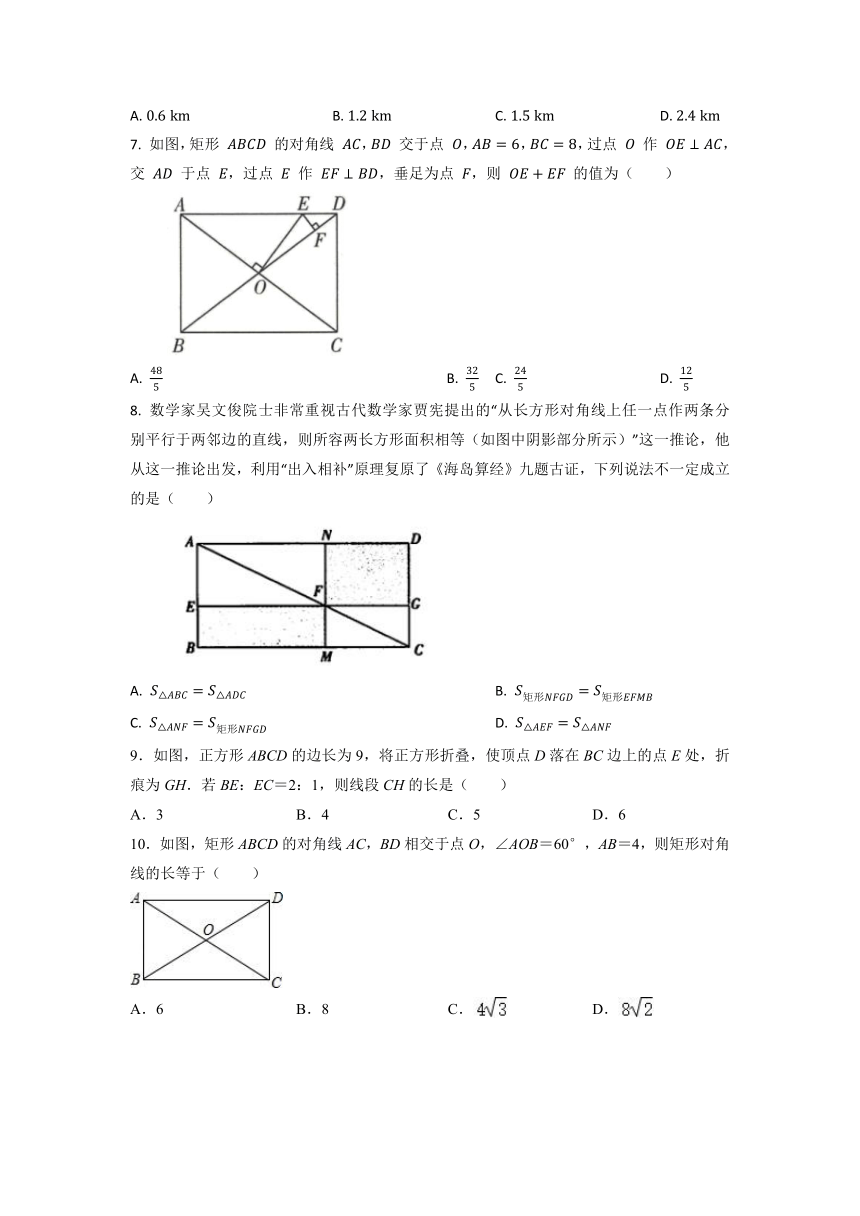
7. 如图,矩形 的对角线 , 交于点 ,,,过点 作 ,交 于点 ,过点 作 ,垂足为点 ,则 的值为( )
A. B. C. D.
8. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图中阴影部分所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,下列说法不一定成立的是( )
A. B.
C. D.
9.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
A.3 B.4 C.5 D.6
10.如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4,则矩形对角线的长等于( )
A.6 B.8 C. D.
二、填空题
11. 中,,点 为 的中点,若 ,则 .
12. 已知 ,,小明按如下步骤作图:
①以 为圆心, 长为半径作弧,以 为圆心, 长为半径作弧,两弧相交于点 ;
②连接 ,.
则四边形 为 .
13. 如图,在正方形 中,点 为 上一点, 与 相交于点 ,若 ,则 等于 度.
14.如图,在菱形ABCD中,点F在AC上,DF的延长线交AB于点E,若∠FBC=80°,则∠AED的度数为 .
15.平行四边形ABCD一内角的平分线与边相交并把这条边分成5cm,7cm的两条线段,则平行四边形ABCD的周长是 cm.
16. 如图,在矩形 中(), 是 上一点,且 ,,垂足为 .在下列结论中① ;② ;③ ;④ .一定正确的是 (把正确的序号写在横线上).
17. 如图放置的两个正方形的边长分别为 和 ,点 为 中点,则 的长为 .
三、解答题
18. 把如图所示的五个边长为 的小正方形,剪成三块拼成一个大正方形.
(1)求大正方形的边长;
(2)给出你的拼法.
19.(6分)如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.猜想四边形AECF的形状,并说明你的理由.
20.如图,菱形ABCD对角线AC与BD的交于点O,CD=10,OD=6,过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长.
(2)求四边形OBEC的面积.
21. 已知平行四边形 的对角线 与 相交于点 ,这个平行四边形的周长是 ,且 的周长比 的周长小 ,求边 和 的长.
22. 如图,在平行四边形 中,对角线 与 相交于点 ,点 , 分别为 , 的中点,延长 至 ,使 ,连接 .
(1)求证:.
(2)当 时,四边形 是什么样的四边形 试说明理由.
23. 完成下列问题.
(1)如图①,纸片平行四边形 中,,.过点 作 ,垂足为 ,沿 剪下 ,将它平移至 的位置,拼成四边形 ,则四边形 的形状为()
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图②,在(1)中的四边形纸片 中,在 上取一点 ,使 ,剪下 ,将它平移至 的位置,拼成四边形 .
①求证:四边形 是菱形;
②求:四边形 的两条对角线的长.
24.(10分)如图1,在平行四边形ABCD中,BE平分∠ABC交CD于点E,CF⊥AD于点F,交BE于点G,且CF=CE,连接EF.
(1)若CD=5,DF=3,求BC的长度;
(2)如图2,若CM平分∠DCF交BE于点M,CN⊥BE于点N,求证:CM+EF=NE.
25.如图, ABCD的对角线AC,BD相交于点O,E,F分别为OD,OB的中点,求证:CE∥AF.
26.如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA 和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求四边形ADCE的面积.
班级______ 姓名_______ 学号_____
一、选择题
1. 如果平行四边形 的 ,那么另三个内角 ,, 分别是 ( )
A. ,, B. ,,
C. ,, D. ,,
2. 已知平行四边形 中,,则 ( )
A. B. C. D. 或
3. 在 中,, 于 , 为 的中点,,则 的长为( )
A. B. C. D.
4.如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则 ABCD的周长是( )
A.24 B.18 C.16 D.12
5.如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A.(6,3) B.(3,6) C.(0,6) D.(6,6)
6. 如图,公路 , 互相垂直,公路 的中点 与点 被湖隔开,若测得 的长为 ,则 , 两点间的距离为( )
A. B. C. D.
7. 如图,矩形 的对角线 , 交于点 ,,,过点 作 ,交 于点 ,过点 作 ,垂足为点 ,则 的值为( )
A. B. C. D.
8. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图中阴影部分所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,下列说法不一定成立的是( )
A. B.
C. D.
9.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
A.3 B.4 C.5 D.6
10.如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4,则矩形对角线的长等于( )
A.6 B.8 C. D.
二、填空题
11. 中,,点 为 的中点,若 ,则 .
12. 已知 ,,小明按如下步骤作图:
①以 为圆心, 长为半径作弧,以 为圆心, 长为半径作弧,两弧相交于点 ;
②连接 ,.
则四边形 为 .
13. 如图,在正方形 中,点 为 上一点, 与 相交于点 ,若 ,则 等于 度.
14.如图,在菱形ABCD中,点F在AC上,DF的延长线交AB于点E,若∠FBC=80°,则∠AED的度数为 .
15.平行四边形ABCD一内角的平分线与边相交并把这条边分成5cm,7cm的两条线段,则平行四边形ABCD的周长是 cm.
16. 如图,在矩形 中(), 是 上一点,且 ,,垂足为 .在下列结论中① ;② ;③ ;④ .一定正确的是 (把正确的序号写在横线上).
17. 如图放置的两个正方形的边长分别为 和 ,点 为 中点,则 的长为 .
三、解答题
18. 把如图所示的五个边长为 的小正方形,剪成三块拼成一个大正方形.
(1)求大正方形的边长;
(2)给出你的拼法.
19.(6分)如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.猜想四边形AECF的形状,并说明你的理由.
20.如图,菱形ABCD对角线AC与BD的交于点O,CD=10,OD=6,过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长.
(2)求四边形OBEC的面积.
21. 已知平行四边形 的对角线 与 相交于点 ,这个平行四边形的周长是 ,且 的周长比 的周长小 ,求边 和 的长.
22. 如图,在平行四边形 中,对角线 与 相交于点 ,点 , 分别为 , 的中点,延长 至 ,使 ,连接 .
(1)求证:.
(2)当 时,四边形 是什么样的四边形 试说明理由.
23. 完成下列问题.
(1)如图①,纸片平行四边形 中,,.过点 作 ,垂足为 ,沿 剪下 ,将它平移至 的位置,拼成四边形 ,则四边形 的形状为()
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图②,在(1)中的四边形纸片 中,在 上取一点 ,使 ,剪下 ,将它平移至 的位置,拼成四边形 .
①求证:四边形 是菱形;
②求:四边形 的两条对角线的长.
24.(10分)如图1,在平行四边形ABCD中,BE平分∠ABC交CD于点E,CF⊥AD于点F,交BE于点G,且CF=CE,连接EF.
(1)若CD=5,DF=3,求BC的长度;
(2)如图2,若CM平分∠DCF交BE于点M,CN⊥BE于点N,求证:CM+EF=NE.
25.如图, ABCD的对角线AC,BD相交于点O,E,F分别为OD,OB的中点,求证:CE∥AF.
26.如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA 和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求四边形ADCE的面积.
