2022-2023学年京改版七年级数学上册第二章 一元一次方程 单元综合练(含解析)
文档属性
| 名称 | 2022-2023学年京改版七年级数学上册第二章 一元一次方程 单元综合练(含解析) | 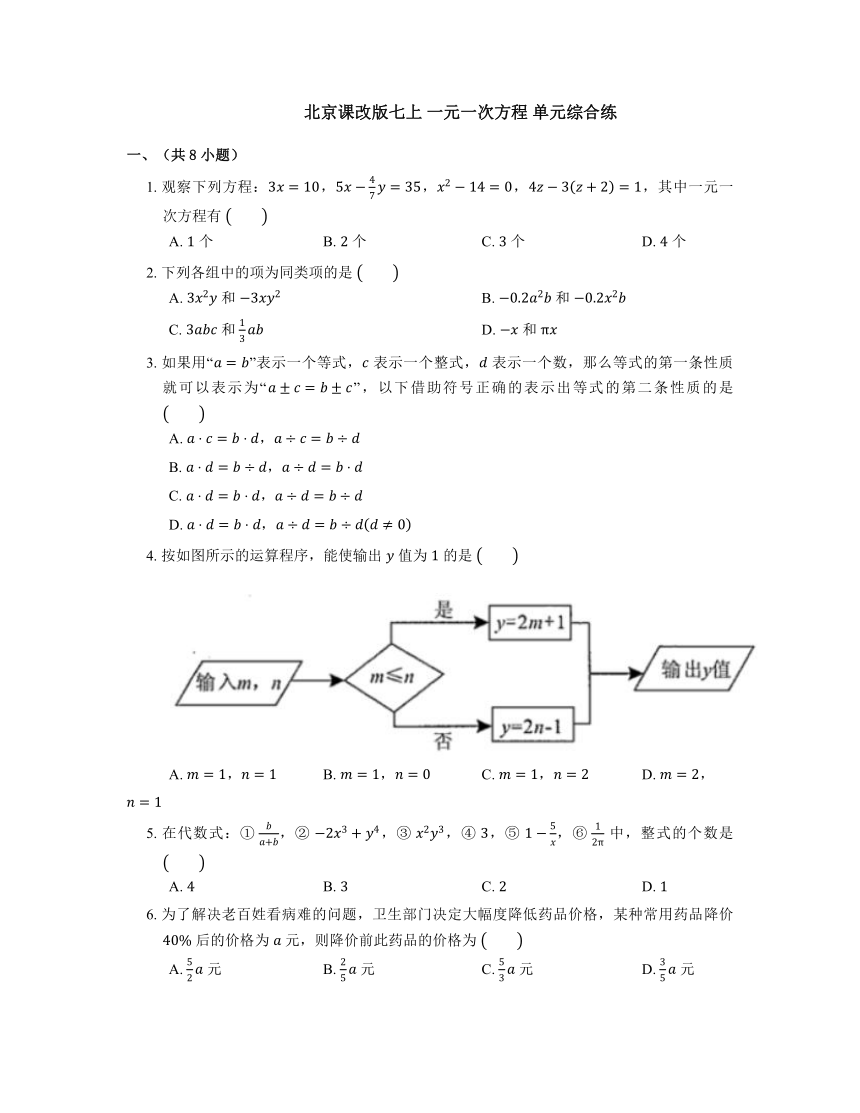 | |
| 格式 | docx | ||
| 文件大小 | 96.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-12 20:44:00 | ||
图片预览



文档简介
北京课改版七上 一元一次方程 单元综合练
一、(共8小题)
1. 观察下列方程:,,,,其中一元一次方程有
A. 个 B. 个 C. 个 D. 个
2. 下列各组中的项为同类项的是
A. 和 B. 和
C. 和 D. 和
3. 如果用“”表示一个等式, 表示一个整式, 表示一个数,那么等式的第一条性质就可以表示为“”,以下借助符号正确的表示出等式的第二条性质的是
A. ,
B. ,
C. ,
D. ,
4. 按如图所示的运算程序,能使输出 值为 的是
A. , B. , C. , D. ,
5. 在代数式:① ,② ,③ ,④ ,⑤ ,⑥ 中,整式的个数是
A. B. C. D.
6. 为了解决老百姓看病难的问题,卫生部门决定大幅度降低药品价格,某种常用药品降价 后的价格为 元,则降价前此药品的价格为
A. 元 B. 元 C. 元 D. 元
7. 阅读:关于 方程 在不同的条件下解的情况如下:()当 时,有唯一解 ;()当 , 时有无数解;()当 , 时无解.请你根据以上知识作答:
已知关于 的方程 无解,则 的值是
A. B. C. D.
8. 若当 时,代数式 的值为 ,则当 时,代数式 值为
A. B. C. D.
二、(共9小题)
9. 使方程等号左右两边相等的 叫做方程的解;求 的过程叫做解方程.
10. 一个圆的周长为 ,则字母 表示的意义为 .
11. 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的 ,另一根露出水面的长度是它的 .两根铁棒长度之和为 ,此时木桶中水的深度是 .
12. 对于这样的等式:若 ,则
()当 时, ;
() .
13. 方程 中,常数项是 ,三次项是 .
14. 如果将方程 变形为用含 的式子表示 ,则 .
15. 已知方程 是关于 的一元一次方程,则 应满足的条件是 .
16. 某同学在计算 时,误将“”看成了“”,求得的结果是 ,已知 ,则 的正确结果为 .
17. 已知 是方程 的解,那么关于 的方程 的解是 .
三、(共7小题)
18. 七年级有三个班,这三个班在参加植树造林活动中,一班植了 棵树,二班植的树比一班的 倍少 棵,三班植的树比一班的 多 棵.求二班比三班多植树多少棵.
19. 已知方程 是关于 的一元一次方程,求 的值.
20. 某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本 元;如果按原价的九折出售,那么每件盈利 元,则这种衬衫的原价是多少
21. 运用等式的性质解下列方程并检验:
(1);
(2);
(3);
(4).
22. 已知 是关于 的方程 的解,求关于 的方程 的解.
23. 已知当 时,多项式 的值为 .
(1)求 的值.
(2)若当 时,该多项式的值为 .
①当 时,求该多项式的值;
②若 ,,,试比较 与 的大小,并说明理由.
24. 一般地,当 时,,可是有这样一个神奇的等式:(其中 , 为任意实数,且 ),你相信它的正确性吗
(1)选两组你喜欢的值,观察上述等式是否成立.
①当 , 时,等式 (填“成立”或“不成立”);
②当 , 时,等式 (填“成立”或“不成立”);
(2)题中所给的等式是否恒成立,作出判断,并说明理由.
答案
一
1. B
2. D
【解析】 和 所含字母相同,但相同字母的指数不相同,所以不是同类项;
和 所含字母不同,所以不是同类项;
和 所含字母不同,所以不是同类项;
和 所含字母相同,并且相同字母的指数也相同,所以是同类项,
故选D.
3. D
4. D
5. A
6. C
7. A
8. D
二
9. 未知数的值,方程的解
10. 圆的半径
【解析】一个圆的周长为 ,则字母 表示的意义为圆的半径.
11.
12. ,
【解析】()因为 ,
所以当 时,,即 .
()因为 ,
所以当 时,,即 .
13. ,
14.
15.
【解析】方程化为 ,,
.
16.
【解析】根据题意得,
17.
【解析】将 代入已知方程得:,
去分母得:,
去括号,得 ,
解得 ,
把 代入方程 ,
得 ,
解得 .
三
18. 二班植树 棵,三班植树 棵.
二班比三班多植树(单位:棵),
19. 由题意可知:,
所以 ,
则 .
又因为 ,
所以 .
所以 .
20. 设这种衬衫的原价是 元.
根据题意,得
解得
答:这种衬衫的原价是 元.
21. (1) 方程两边同时减去 ,得
于是,得
检验:当 时,左边 右边.
所以 是原方程的解.
(2) 方程两边同时除以 ,得
于是,得
检验:当 时,左边 右边.
所以 是原方程的解.
(3) 方程两边同时减去 ,得
于是,得
检验:当 时,左边 ,
右边 ,
所以 左边 右边.
所以 是原方程的解.
(4) 方程两边同时减去 ,得
于是,得
方程两边同时乘以 ,得
检验:当 时,右边 ,
所以 左边 右边.
所以 是原方程的解.
22. 把 代入方程 ,得
即 .两边加 ,得
两边除以 ,得
把 代入方程 ,得
两边加 ,得
23. (1) 把 代入 ,得 .
(2) ①把 代入 ,得 .
所以 .
把 代入 ,得 .
② ,理由如下:
因为 ,
所以 , 同号.
由①知 ,
所以 ,.
因为 ,
所以 .
因为 ,且 ,
所以 .
所以 .
所以 .
24. (1) ;;成立;;;成立
【解析】例如:
①当 , 时,等式 成立;
②当 , 时,等式 成立.
(2) 题中所给的等式是恒成立的,理由如下:
,
.
等式 成立.
一、(共8小题)
1. 观察下列方程:,,,,其中一元一次方程有
A. 个 B. 个 C. 个 D. 个
2. 下列各组中的项为同类项的是
A. 和 B. 和
C. 和 D. 和
3. 如果用“”表示一个等式, 表示一个整式, 表示一个数,那么等式的第一条性质就可以表示为“”,以下借助符号正确的表示出等式的第二条性质的是
A. ,
B. ,
C. ,
D. ,
4. 按如图所示的运算程序,能使输出 值为 的是
A. , B. , C. , D. ,
5. 在代数式:① ,② ,③ ,④ ,⑤ ,⑥ 中,整式的个数是
A. B. C. D.
6. 为了解决老百姓看病难的问题,卫生部门决定大幅度降低药品价格,某种常用药品降价 后的价格为 元,则降价前此药品的价格为
A. 元 B. 元 C. 元 D. 元
7. 阅读:关于 方程 在不同的条件下解的情况如下:()当 时,有唯一解 ;()当 , 时有无数解;()当 , 时无解.请你根据以上知识作答:
已知关于 的方程 无解,则 的值是
A. B. C. D.
8. 若当 时,代数式 的值为 ,则当 时,代数式 值为
A. B. C. D.
二、(共9小题)
9. 使方程等号左右两边相等的 叫做方程的解;求 的过程叫做解方程.
10. 一个圆的周长为 ,则字母 表示的意义为 .
11. 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的 ,另一根露出水面的长度是它的 .两根铁棒长度之和为 ,此时木桶中水的深度是 .
12. 对于这样的等式:若 ,则
()当 时, ;
() .
13. 方程 中,常数项是 ,三次项是 .
14. 如果将方程 变形为用含 的式子表示 ,则 .
15. 已知方程 是关于 的一元一次方程,则 应满足的条件是 .
16. 某同学在计算 时,误将“”看成了“”,求得的结果是 ,已知 ,则 的正确结果为 .
17. 已知 是方程 的解,那么关于 的方程 的解是 .
三、(共7小题)
18. 七年级有三个班,这三个班在参加植树造林活动中,一班植了 棵树,二班植的树比一班的 倍少 棵,三班植的树比一班的 多 棵.求二班比三班多植树多少棵.
19. 已知方程 是关于 的一元一次方程,求 的值.
20. 某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本 元;如果按原价的九折出售,那么每件盈利 元,则这种衬衫的原价是多少
21. 运用等式的性质解下列方程并检验:
(1);
(2);
(3);
(4).
22. 已知 是关于 的方程 的解,求关于 的方程 的解.
23. 已知当 时,多项式 的值为 .
(1)求 的值.
(2)若当 时,该多项式的值为 .
①当 时,求该多项式的值;
②若 ,,,试比较 与 的大小,并说明理由.
24. 一般地,当 时,,可是有这样一个神奇的等式:(其中 , 为任意实数,且 ),你相信它的正确性吗
(1)选两组你喜欢的值,观察上述等式是否成立.
①当 , 时,等式 (填“成立”或“不成立”);
②当 , 时,等式 (填“成立”或“不成立”);
(2)题中所给的等式是否恒成立,作出判断,并说明理由.
答案
一
1. B
2. D
【解析】 和 所含字母相同,但相同字母的指数不相同,所以不是同类项;
和 所含字母不同,所以不是同类项;
和 所含字母不同,所以不是同类项;
和 所含字母相同,并且相同字母的指数也相同,所以是同类项,
故选D.
3. D
4. D
5. A
6. C
7. A
8. D
二
9. 未知数的值,方程的解
10. 圆的半径
【解析】一个圆的周长为 ,则字母 表示的意义为圆的半径.
11.
12. ,
【解析】()因为 ,
所以当 时,,即 .
()因为 ,
所以当 时,,即 .
13. ,
14.
15.
【解析】方程化为 ,,
.
16.
【解析】根据题意得,
17.
【解析】将 代入已知方程得:,
去分母得:,
去括号,得 ,
解得 ,
把 代入方程 ,
得 ,
解得 .
三
18. 二班植树 棵,三班植树 棵.
二班比三班多植树(单位:棵),
19. 由题意可知:,
所以 ,
则 .
又因为 ,
所以 .
所以 .
20. 设这种衬衫的原价是 元.
根据题意,得
解得
答:这种衬衫的原价是 元.
21. (1) 方程两边同时减去 ,得
于是,得
检验:当 时,左边 右边.
所以 是原方程的解.
(2) 方程两边同时除以 ,得
于是,得
检验:当 时,左边 右边.
所以 是原方程的解.
(3) 方程两边同时减去 ,得
于是,得
检验:当 时,左边 ,
右边 ,
所以 左边 右边.
所以 是原方程的解.
(4) 方程两边同时减去 ,得
于是,得
方程两边同时乘以 ,得
检验:当 时,右边 ,
所以 左边 右边.
所以 是原方程的解.
22. 把 代入方程 ,得
即 .两边加 ,得
两边除以 ,得
把 代入方程 ,得
两边加 ,得
23. (1) 把 代入 ,得 .
(2) ①把 代入 ,得 .
所以 .
把 代入 ,得 .
② ,理由如下:
因为 ,
所以 , 同号.
由①知 ,
所以 ,.
因为 ,
所以 .
因为 ,且 ,
所以 .
所以 .
所以 .
24. (1) ;;成立;;;成立
【解析】例如:
①当 , 时,等式 成立;
②当 , 时,等式 成立.
(2) 题中所给的等式是恒成立的,理由如下:
,
.
等式 成立.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
