5.2.2平行线的判定 同步练习(无答案)2022-2023学年人教版数学七年级下册
文档属性
| 名称 | 5.2.2平行线的判定 同步练习(无答案)2022-2023学年人教版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 402.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-12 00:00:00 | ||
图片预览



文档简介
平行线的判定 同步精练
一、单选题
1.如图,直线a,b被直线l所截,下列条件能判定的是( )
①;②;③;④
A.①② B.①③ C.①④ D.③④
2.如图所示,点E在AC的延长线上,下列条件中不能判断( )
A.∠3=∠4 B.∠1=∠2 C.∠D=∠DCE D.∠D+∠ACD=180°
3.如图,直线a、b被直线c所截,则下列式子:①;②;③;④,能说明的条件的是( )
A.①② B.②④ C.①②③ D.①②③④
4.下列说法正确的是( )
A.在同一平面内,a,b,c是直线,且,则
B.在同一平面内,a,b,c是直线,且,则
C.在同一平面内,a,b,c是直线,且,则
D.在同一平面内,a,b,c是直线,且,则
5.如图,不能推断ABCD的是( )
A. B. C. D.
6.如图,直线,且直线a,b被直线c,d所截,则下列条件可以判定直线的是( )
A. B. C. D.
7.如图,点在的延长线上,下列条件不能判定的是( )
A. B. C. D.
8.在下列说法中,正确的有( )个.
①过一点有且只有一条直线与已知直线平行; ②已知、的两边分别平行,那么;
③垂直于同一条直线的两条直线平行; ④从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
A.3 B.2 C.1 D.0
9.如图,不能确定直线的条件是( )
A. B. C. D.
10.如图,点E在的延长线上,下列条件不能判定的是( )
A. B. C. D.
二、填空题
11.如图,直线ab且直线c与a、b相交,若∠1=70°,则∠2=_____°.
12.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB//DC的条件为_______.
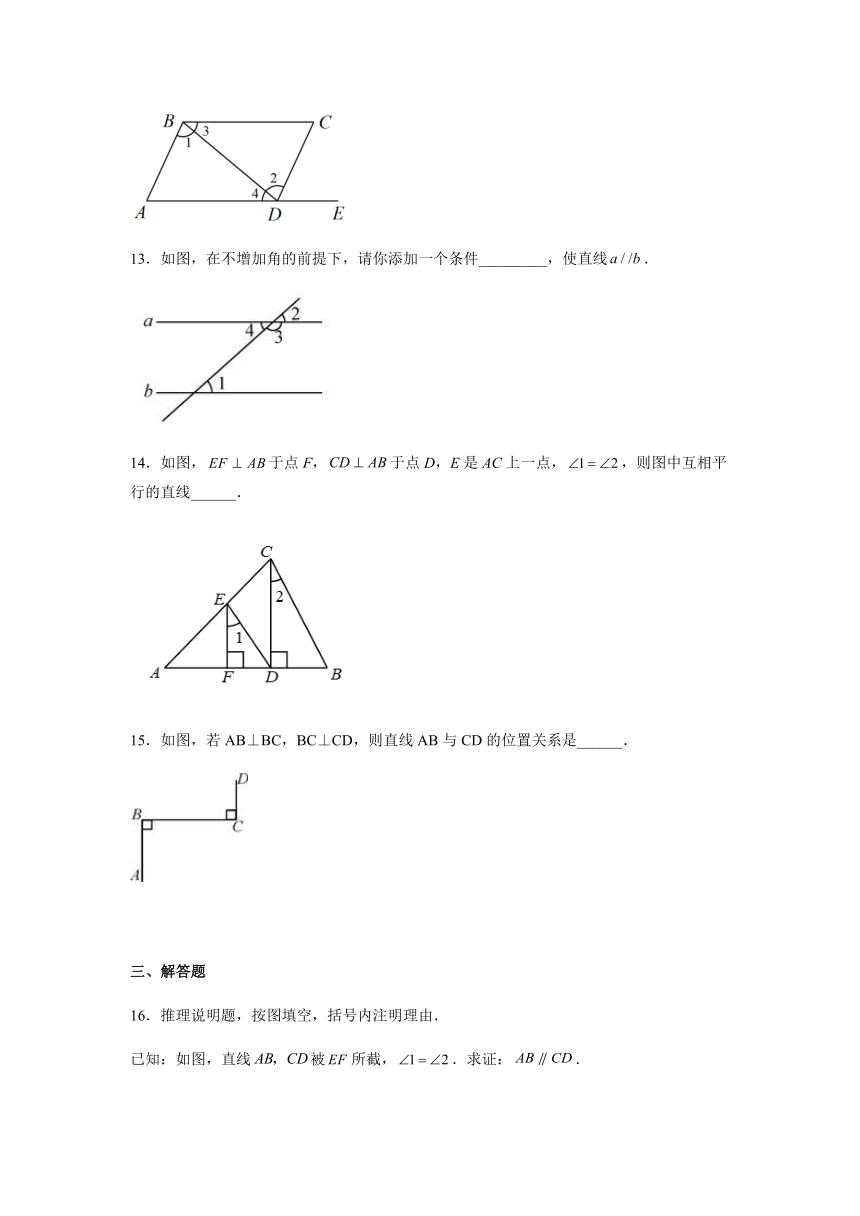
13.如图,在不增加角的前提下,请你添加一个条件_________,使直线.
14.如图,于点F,于点D,E是AC上一点,,则图中互相平行的直线______.
15.如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是______.
三、解答题
16.推理说明题,按图填空,括号内注明理由.
已知:如图,直线被所截,.求证:.
证明:∵( ),
又∵(已知),
∴∠_____=∠______,
∴_____________( ).
17.如图所示,,AC平分.
求证:.
请补充完整下列证明过程.
证明:如图,
∵AC平分(已知)
∴(_______________________)
∵(已知)
∴__________________________________(等量代换)
∴(___________________________________)
18.如图,是上一点,是上一点,是延长线上一点.
(1)如果,可以判断哪两条直线平行?为什么?
(2)如果,可以判断哪两条直线平行?为什么?
(3)如果,可以判断哪两条直线平行?为什么?
19.如图,已知点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D,F,点M,G在AB上,GF交BD于点H,∠BMD+∠ABC=180°,∠1=∠2,求证:MDGF.
下面是小颖同学的思考过程,请补全证明过程并在括号内填上证明依据.
证明:∵BD⊥AC,EF⊥AC,
∴∠BDC=90°,∠EFC=90°(① ).
∴∠BDC=∠EFC(等量代换).
∴BDEF(同位角相等,两直线平行).
∴∠2=∠CBD( ② ).
∵∠1=∠2(已知).
∴∠1=∠CBD(等量代换).
∴③ (内错角相等,两直线平行).
∵∠BMD+∠ABC=180°(已知),
∴MDBC(④ ).
∴MDGF(⑤ ).
20.已知:如图,直线被所截, ,
求证: .
证法1:如图, 与交于
( )
又( )
( )
( )
证法2:如图,
( )
又( )
( )
( )
证法3:如图,
( )
( )
又( )
( )
( )
一、单选题
1.如图,直线a,b被直线l所截,下列条件能判定的是( )
①;②;③;④
A.①② B.①③ C.①④ D.③④
2.如图所示,点E在AC的延长线上,下列条件中不能判断( )
A.∠3=∠4 B.∠1=∠2 C.∠D=∠DCE D.∠D+∠ACD=180°
3.如图,直线a、b被直线c所截,则下列式子:①;②;③;④,能说明的条件的是( )
A.①② B.②④ C.①②③ D.①②③④
4.下列说法正确的是( )
A.在同一平面内,a,b,c是直线,且,则
B.在同一平面内,a,b,c是直线,且,则
C.在同一平面内,a,b,c是直线,且,则
D.在同一平面内,a,b,c是直线,且,则
5.如图,不能推断ABCD的是( )
A. B. C. D.
6.如图,直线,且直线a,b被直线c,d所截,则下列条件可以判定直线的是( )
A. B. C. D.
7.如图,点在的延长线上,下列条件不能判定的是( )
A. B. C. D.
8.在下列说法中,正确的有( )个.
①过一点有且只有一条直线与已知直线平行; ②已知、的两边分别平行,那么;
③垂直于同一条直线的两条直线平行; ④从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
A.3 B.2 C.1 D.0
9.如图,不能确定直线的条件是( )
A. B. C. D.
10.如图,点E在的延长线上,下列条件不能判定的是( )
A. B. C. D.
二、填空题
11.如图,直线ab且直线c与a、b相交,若∠1=70°,则∠2=_____°.
12.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB//DC的条件为_______.
13.如图,在不增加角的前提下,请你添加一个条件_________,使直线.
14.如图,于点F,于点D,E是AC上一点,,则图中互相平行的直线______.
15.如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是______.
三、解答题
16.推理说明题,按图填空,括号内注明理由.
已知:如图,直线被所截,.求证:.
证明:∵( ),
又∵(已知),
∴∠_____=∠______,
∴_____________( ).
17.如图所示,,AC平分.
求证:.
请补充完整下列证明过程.
证明:如图,
∵AC平分(已知)
∴(_______________________)
∵(已知)
∴__________________________________(等量代换)
∴(___________________________________)
18.如图,是上一点,是上一点,是延长线上一点.
(1)如果,可以判断哪两条直线平行?为什么?
(2)如果,可以判断哪两条直线平行?为什么?
(3)如果,可以判断哪两条直线平行?为什么?
19.如图,已知点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D,F,点M,G在AB上,GF交BD于点H,∠BMD+∠ABC=180°,∠1=∠2,求证:MDGF.
下面是小颖同学的思考过程,请补全证明过程并在括号内填上证明依据.
证明:∵BD⊥AC,EF⊥AC,
∴∠BDC=90°,∠EFC=90°(① ).
∴∠BDC=∠EFC(等量代换).
∴BDEF(同位角相等,两直线平行).
∴∠2=∠CBD( ② ).
∵∠1=∠2(已知).
∴∠1=∠CBD(等量代换).
∴③ (内错角相等,两直线平行).
∵∠BMD+∠ABC=180°(已知),
∴MDBC(④ ).
∴MDGF(⑤ ).
20.已知:如图,直线被所截, ,
求证: .
证法1:如图, 与交于
( )
又( )
( )
( )
证法2:如图,
( )
又( )
( )
( )
证法3:如图,
( )
( )
又( )
( )
( )
