第四单元《巧手小工匠——认识多边形》(同步练习)四年级下册数学青岛版(无答案)
文档属性
| 名称 | 第四单元《巧手小工匠——认识多边形》(同步练习)四年级下册数学青岛版(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 68.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-12 15:42:01 | ||
图片预览




文档简介
青岛版数学四年级下册同步练习
第四单元
《巧手小工匠——认识多边形》
学校:___________姓名:___________班级:__________
一、选择题
1.天天已有两根小棒,分别是4m和6cm,地想从下面的小小棒中再选一根围成一个三角形,应该选( )长的小棒。
A.5cm B.10cm C.12cm
2.一个三角形最小的锐角是50度,这个三角形一定是( )三角形。
A.钝角 B.直角 C.锐角
3.a、b、c是三角形的三条边,那么它们之间的关系不正确的是( )。
A.a+b>c B.a+b<c C.a+c>b
4.下面说法错误的是( )。
A.平行四边形有无数条高
B.有一组对边平行的四边形是梯形
C.用长度分别是2dm、2dm、3dm的三根小棒可以围成一个等腰三角形
5.等腰三角形的两边分别为4cm和2cm,则这个三角形的周长是( )。
A.10cm B.8cm C.8cm或10cm
6.下面哪组中的三条线段可以围成一个三角形( )。
A. B. C.
7.一个等腰三角形的两条边分别是5厘米、10厘米,它的周长是( )厘米。
A.20 B.25 C.20或25
8.小明要用三根木条钉成一个三角形,他已经选好了11厘米、5厘米长的两根木条,第三根木条的长度最短是( )厘米。(取整厘米数)
A.6 B.7 C.11
二、填空题
9.一个等腰三角形的底角是30°,它的顶角是( )°,按角分这是个( )三角形。
10.求角的度数,已知∠1=35°,那么∠2=( )°,∠3=( )°,∠4=( )°。
11.在等腰三角形中,当底角是43°的时候,那么它的顶角是( )°,按角来分它属于( )三角形。
12.如图中有( )个三角形,( )个平行四边形,( )个梯形。
13.一个等腰三角形,它的一条边长是5厘米,另一条边长是6厘米,这个三角形的周长是( )厘米。一个等边三角形的周长是24厘米,它一条边的长是( )厘米。
14.小明做一个等腰三角形框架,两条边长分别是5厘米和10厘米,这个框架至少需要( )厘米的木条。
15.小华用小棒拼一个三角形,其中2根的长分别是6厘米、3厘米,第三根最长是( )厘米。(填写整厘米数)
16.一个等腰三角形,它的底角是30°,顶角是( )°。如果它的周长是8米,一条腰长m米,它的底长( )米。
三、判断题
17.连接相对顶点的弧线把平行四边形分成了两部分,两部分的周长一样。( )
18.小明说他做了一个等腰三角形,这个等腰三角形的一个底角92°。( )
19.小明说他从4根分别是4厘米、5厘米、6厘米、8厘米的小棒中,任意选出3根,一定能围成一个三角形。( )
20.任何两个等底等高的梯形,都一定能拼成一个平行四边形。( )
21.有三条线段分别长3cm、7cm、10cm,它们能组成一个三角形。( )
四、图形计算
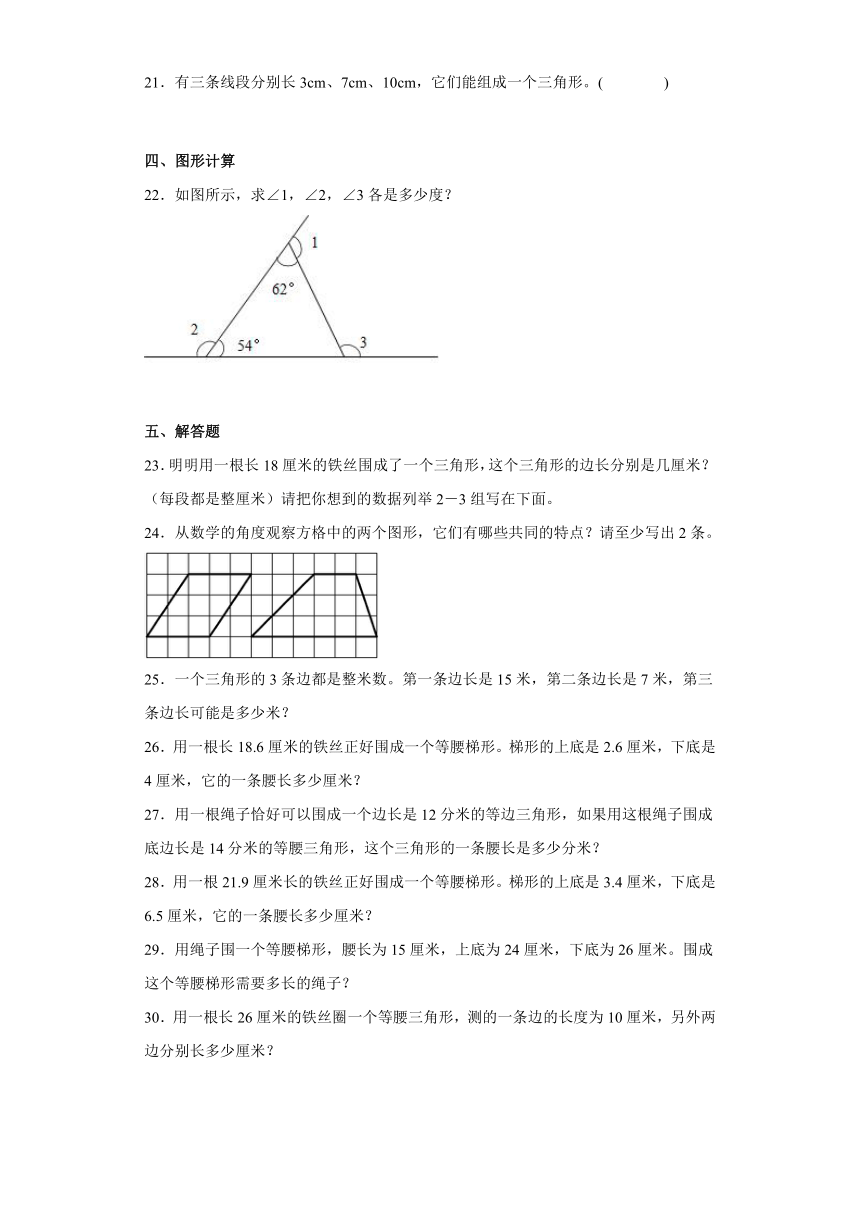
22.如图所示,求∠1,∠2,∠3各是多少度?
五、解答题
23.明明用一根长18厘米的铁丝围成了一个三角形,这个三角形的边长分别是几厘米?(每段都是整厘米)请把你想到的数据列举2-3组写在下面。
24.从数学的角度观察方格中的两个图形,它们有哪些共同的特点?请至少写出2条。
25.一个三角形的3条边都是整米数。第一条边长是15米,第二条边长是7米,第三条边长可能是多少米?
26.用一根长18.6厘米的铁丝正好围成一个等腰梯形。梯形的上底是2.6厘米,下底是4厘米,它的一条腰长多少厘米?
27.用一根绳子恰好可以围成一个边长是12分米的等边三角形,如果用这根绳子围成底边长是14分米的等腰三角形,这个三角形的一条腰长是多少分米?
28.用一根21.9厘米长的铁丝正好围成一个等腰梯形。梯形的上底是3.4厘米,下底是6.5厘米,它的一条腰长多少厘米?
29.用绳子围一个等腰梯形,腰长为15厘米,上底为24厘米,下底为26厘米。围成这个等腰梯形需要多长的绳子?
30.用一根长26厘米的铁丝圈一个等腰三角形,测的一条边的长度为10厘米,另外两边分别长多少厘米?
参考答案:
1.A
【分析】根据三角形任意两边之和大于第三边,进行分析。
【详解】A.4+5>6,可以;
B.4+6=10,不可以;
C.4+6<12,不可以。
故答案为:A
【点睛】关键是掌握三角形三边之间的关系。
2.C
【分析】三角形内角和180度,假设有两个角都是50度,让一个角尽可能的大,再根据三角形分类标准确定三角形类型即可。
【详解】180-50-50=80(度)
这个三角形一定是锐角三角形。
故答案为:C
【点睛】关键是掌握三角形内角和以及三角形按角分类标准。
3.B
【分析】根据三角形三边关系:三角形的任意两边之和大于第三边;进行分析即可得出结论。
【详解】A.a+b>c,两边之和大于第三边,符合三角形三边关系,本选项正确;
B.a+b<c,两边之和小于第三边,不符合三角形三边关系,所以本选项不正确;
C.a+c>b,两边之和大于第三边,符合三角形三边关系,本选项正确。
故答案为:B
【点睛】熟练掌握三角形三边关系,是解答此题的关键。
4.B
【分析】先对每个选项中的说法进行分析并判断,然后选择正确的一项即可。
A.从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,依此判断;
B.只有一组对边平行的四边形叫做梯形,依此判断;
C.等腰三角形的两腰相等,三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此判断即可。
【详解】A.平行四边形有无数条高,即原说法正确;
B.只有一组对边平行的四边形是梯形,即原说法错误;
C.2dm+2dm>3dm,3dm-2dm<2dm,2dm=2dm,即用长度分别是2dm、2dm、3dm的三根小棒可以围成一个等腰三角形,即原说法正确。
故答案为:B
【点睛】此题考查的是平行四边形的高,梯形的特点,以及三角形3条边的关系,应熟练掌握。
5.A
【分析】根据等腰三角形的性质,当腰长是2cm时,则三角形的三边是2cm,2cm,4cm,2cm+2cm=4cm不满足三角形的三边关系;当腰长是4cm时,三角形的三边是4cm,4cm,2cm,4cm+2cm=6cm>4cm,能构成三角形,据此求出三角形的周长即可。
【详解】根据等腰三角形的性质得,三角形的腰长是4cm,底是2cm,
周长:
故答案为:A
【点睛】本题考查了等腰三角形的性质和三角形的三边关系。
6.B
【分析】判断三角形能否构成,关键是看三条线段是否满足:任意两边之和是否大于第三边,但通常不需要一一验证,其简便方法是将较短两边之和与较长边比较。
【详解】A.2+6<10,不能围成三角形;
B.3+4>5,能围成三角形;
C.8+8=16,不能围成三角形。
故答案为:B
【点睛】本题主要考查三角形的三边关系:三角形任意两边之和大于第三边。
7.B
【分析】在三角形中,两边之和大于第三边,所以这个等腰三角形的腰为10厘米,那么把三角形的三条边相加即可得到这个等腰三角形的周长,据此列式解答。
【详解】因为5+5=10,
所以5厘米的边只能是底。
它的周长是:10+10+5
=20+5
=25(厘米)
故答案为:B
【点睛】此题主要考查三角形的三边关系以及三角形周长的计算方法。
8.B
【分析】任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,此题依此选择即可。
【详解】1-5=6(厘米);11+5=16(厘米);
6厘米<第三边的长度<16厘米
6+1=7(厘米)
因此第三根木条的长度最短是7厘米。
故答案为:B
【点睛】熟练掌握三角形三条边之间的关系是解答本题的关键。
9. 120 钝角
【分析】等腰三角形的两腰相等,两个底角都相等,三角形的内角和为180°,因此用180°减去2个30°即可得到顶角的度数,依此计算并根据三角形的分类标准填空,有一个角是钝角的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,三个角都是锐角的三角形是锐角三角形。
【详解】30°+30°=60°
180°-60°=120°
120°>90°,因此按角分这是一个钝角三角形。
一个等腰三角形的底角是30°,它的顶角是(120)°,按角分这是个(钝角)三角形。
【点睛】此题考查的是三角形的分类标准,等腰三角形的特点,以及三角形的内角和,应熟练掌握。
10. 35 55 55
【分析】长方形中有4个直角,直角是90°,因此用90°减∠1的度数即可计算出∠3的度数;
三角形的内角和是180°,因此用180°减去90°,再减去∠3的度数即可得到∠2的度数;
用90°减∠2的度数即可计算出∠4的度数;依此计算。
【详解】∠3=90°-35°=55°;
∠2=180°-90°-55°=90°-55°=35°;
∠4=90°-35°=55°。
【点睛】解答此题的关键是要熟练掌握长方形的特点,以及熟记三角形的内角和。
11. 94 钝角
【分析】三个角都是锐角的三角形,叫锐角三角形;有一个角是直角的三角形,叫直角三角形;有一个角是钝角的三角形,叫钝角三角形;等腰三角形两底角相等,用三角形的内角和减去两个底角的度数,就是顶角的度数,然后按照角的分类方法确定它是什么三角形即可。
【详解】180°-43°-43°
=137°-43°
=94°
在等腰三角形中,当底角是43°的时候,那么它的顶角是(94)°,按角来分它属于(钝角)三角形。
【点睛】熟悉等腰三角形的特征是解答此题的关键。
12. 5 2 6
【分析】三条边围成的图形是三角形,平行四边形的两组对边分别平行,梯形的一组对边平行,另一组对边不平行。根据图形的特点进行解答。
【详解】根据分析可知,
图中有5个三角形,2个平行四边形,6个梯形。
【点睛】数梯形个数时易错,注意按一定顺序不重不漏地数是解题的关键。
13. 16##17 8
【分析】根据等腰三角形的两条腰相等,先求出另一条边是多少厘米,然后即可求出等腰三角形的周长;等边三角形的三条边长都相等,用周长除以3即可求出边长是多少厘米。
【详解】两条腰都是5厘米时,
周长:5+5+6
=10+6
=16(厘米)
两条腰都是6厘米时,
周长:6+6+5
=12+5
=17(厘米)
24÷3=8(厘米)
【点睛】此题主要考查对等腰三角形和等边三角形的认识。
14.25
【分析】等腰三角形的两腰相等,三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边;依此计算出第三条边最短的长度,然后再计算出这个等腰三角形的周长即可。
【详解】当5厘米为腰长时,5+5=10(厘米),此种情况不满足;
当10厘米为腰长时,5厘米+10厘米>10厘米;10厘米-5厘米<10厘米
10+10+5=25(厘米)
【点睛】此题考查的是三角形周长的计算,等腰三角形的特点,以及三角形3条边的关系,应熟练掌握。
15.8
【分析】根据三角形三边关系:任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,由此计算并解答即可。
【详解】6-3<第三边<6+3,
所以:3<第三边<9,
即第三边的取值在3~9厘米(不包括3厘米和9厘米),
因为三根小棒都是整厘米数,所以第三根小棒最短是:3+1=4(厘米)
最长是:9-1=8(厘米)。
【点睛】此题关键是根据三角形三边关系进行分析、解答。
16. 120 8-2m
【分析】因为三角形的内角和是180°,该三角形是等腰三角形,它的底角是30°,因为等腰三角形两个底角相等,顶角是180°-30°-30°=120°;
求等腰三角形的底边长度,用等腰三角形的周长减去两条腰长即可解答。
【详解】180°-30°-30°
=150°-30°
=120°
8-m-m=(8-2m)米
一个等腰三角形,它的底角是30°,顶角是120°。如果它的周长是8米,一条腰长m米,它的底长8-2m米。
【点睛】此题考查了三角形的内角和,用到的知识点:等腰三角形两底角相等,两腰长相等。
17.√
【分析】根据平行四边形的性质,平行四边形的对边相等,分别看分成的两部分的周长都有哪几部分围成,据此判断。
【详解】平行四边形对边相等,分成两部分的周长分别由平行四边形的一组对边和一条共同的弧围成,所以两部分的周长一样。
故答案为:√
【点睛】解答本题的关键是熟练掌握平行四边形的性质和周长的意义。
18.×
【分析】等腰三角形的两个底角度数相等;三角形的内角和等于180°,据此判断即可。
【详解】两个底角的度数和是92°×2=184°,与三角形的内角和等于180°矛盾。所以原题干说法错误。
故答案为:×
【点睛】本题考查三角形的内角和,明确等腰三角形的两个底角度数相等是解题的关键。
19.√
【分析】根据三角形三边关系:任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,进行解答。
【详解】如:4+5=9(厘米)>8厘米,
所以小明说他从4根分别是4厘米、5厘米、6厘米、8厘米的小棒中,任意选出3根,一定能围成一个三角形,此说法正确。
故答案为:√
【点睛】本题考查了三角形三边关系的灵活应用。
20.×
【分析】两个完全一样的梯形能拼成平行四边形,两个等底等高的梯形在形状完全一样时,可拼成平行四边形。据此解答。
【详解】两个完全相同的梯形才能拼成一个平行四边形;当两个梯形等底等高时,由于梯形的面积=(上底+下底)×高÷2;题干不能确定两个梯形的形状是完全相同的,故不一定能拼成一个平行四边形。
故答案为:×
【点睛】本题主要考查了梯形和平行四边形的关系。要明确两个完全相同的梯形才能拼成一个平行四边形。
21.×
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】3+7=10
则长3cm、7cm、10cm的三条线段不能组成一个三角形。
故答案为:×。
【点睛】本题考查三角形的三边关系,解题时只需要判断较短的两条边的长度和与最长的那条边的长度之间的大小关系即可。
22.∠1=118°,∠2=126°,∠3=116°
【分析】三角形的内角和是180度,则∠3的邻补角=180°-54°-62°=64°,再根据平角等于180°,求出∠1、∠2、∠3各是多少度即可。
【详解】180°-54°-62°
=126°-62°
=64°
∠1=180°-62°=118°
∠2=180°-54°=126°
∠3=180°-64°=116°
答:∠1=118°,∠2=126°,∠3=116°。
23.8厘米、6厘米、4厘米;或5厘米、6厘米、7厘米;或8厘米、5厘米、5厘米;(答案不唯一)
【分析】根据题意可知,三角形的周长是18厘米;三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此进行解答即可。
【详解】假设三角形的两边分别为8厘米、6厘米,则第三边为:18-8-6=4(厘米)
6厘米+4厘米>8厘米,8厘米-4厘米<6厘米,因此这个三角形的边长分别是8厘米、6厘米、4厘米;
假设三角形的两边分别为5厘米、6厘米,则第三边为:18-5-6=7(厘米)
6厘米+5厘米>7厘米,7厘米-6厘米<6厘米,因此这个三角形的边长分别是5厘米、6厘米、7厘米;
假设三角形的两边分别为8厘米、5厘米,则第三边为:18-5-8=5(厘米)
5厘米+5厘米>8厘米,8厘米-5厘米<5厘米,因此这个三角形的边长分别是8厘米、5厘米、5厘米。
答:这个三角形的边长分别是8厘米、6厘米、4厘米;或5厘米、6厘米、7厘米;或8厘米、5厘米、5厘米。
【点睛】此题考查的是三角形的周长,以及三角形三条边之间的关系,应熟练掌握。
24.见详解
【分析】两组对边分别平行的四边形叫做平行四边形;只有一组对边平行的四边形叫做梯形;
平行四边形和梯形共同的特点是:都是由四条线段围成的图形,所以都是四边形;至少有一组对边平行;任意一个四边形的内角和都是360度,所以它们四个内角的和都是360度;
不同点是:平行四边形的两组对边平行且相等,梯形的上底和下底只平行不相等,两条腰不平行也不一定相等。
【详解】平行四边形和梯形的共同特点:
(1)它们都是四边形;
(2)它们内角和都是360度。(答案不唯一)
【点睛】熟练掌握梯形和平行四边形的特点是解答此题的关键。
25.9米;10米;11米;12米;13米;14米;15米;16米;17米;18米;19米;20米;21米
【分析】根据三角形的特征,三角形任意两边的和大于第三边,任意两边的差小于第三边,据此解答。
【详解】15+7=22(米)
15-7=8(米)
所以8米<三角形的第三边<22米
答:第三条边长可能是9米、10米、11米、12米、13米、14米、15米、16米、17米、18米、19米、20米、21米。
【点睛】此题主要考查对三角形的特征的认识。
26.3厘米
【分析】用这根铁丝围成一个等腰梯形,这根铁丝的长度等于等腰梯形的周长。等腰梯形的两条腰相等,则等腰梯形的腰长=(周长-上底-下底)÷2,代入数据计算即可。
【详解】(18.6-2.6-4)÷2
=12÷4
=3(厘米)
答:它的一条腰长3厘米。
【点睛】本题关键是熟记等腰梯形周长的公式:等腰梯形的周长=上底+下底+2×腰。
27.11分米
【分析】两个三角形的周长相等,等边三角形的边长乘3等于等边三角形的周长,减去14分米等于等腰三角形两条腰的长度和,再除以2即等于一条腰的长度。
【详解】(12×3-14)÷2
=(36-14)÷2
=22÷2
=11(分米)
答:这个三角形的一条腰长是11分米。
【点睛】本题主要考查学生对三角形的周长和三角形分类知识的掌握。
28.6厘米
【分析】根据等腰图形的特征,梯形的两条腰的长度相等,用一根21.9厘米长的铁丝正好围成一个等腰梯形,也就是这个梯形的周长是21.9厘米,用梯形的周长减去上下底的长度就是两条腰的长度和,用两条腰的长度和除以2即可求出一条腰的长度。
【详解】(21.9-3.4-6.5)÷2
=12÷2
=6(厘米)
答:它的一条腰长6厘米。
【点睛】此题主要考查梯形周长公式的灵活运用,关键是熟记公式。
29.80厘米
【分析】根据等腰梯形的周长=两条腰的长度+上底+下底,据此解答即可。
【详解】
(厘米)
答:围成这个等腰梯形需要80厘米长的绳子。
【点睛】此题主要考查梯形周长公式的灵活运用,关键是明确等腰梯形的两条腰相等。
30.10厘米和6厘米,或者均为8厘米
【分析】当10厘米是腰长时,用26厘米减去两腰的长度,可求出底的长度;当10厘米是底长时,用26厘米减去底的长度,再将差除以2,可求出腰的长度。据此解题。
【详解】①26-2×10
=26-20
=6(厘米)
②(26-10)÷2
=16÷2
=8(厘米)
答:第一种可能,另外两边的长度为10厘米和6厘米;第二种可能,另外两边的长度均为8厘米。
【点睛】本题考查了等腰三角形,两腰相等的三角形是等腰三角形。
第四单元
《巧手小工匠——认识多边形》
学校:___________姓名:___________班级:__________
一、选择题
1.天天已有两根小棒,分别是4m和6cm,地想从下面的小小棒中再选一根围成一个三角形,应该选( )长的小棒。
A.5cm B.10cm C.12cm
2.一个三角形最小的锐角是50度,这个三角形一定是( )三角形。
A.钝角 B.直角 C.锐角
3.a、b、c是三角形的三条边,那么它们之间的关系不正确的是( )。
A.a+b>c B.a+b<c C.a+c>b
4.下面说法错误的是( )。
A.平行四边形有无数条高
B.有一组对边平行的四边形是梯形
C.用长度分别是2dm、2dm、3dm的三根小棒可以围成一个等腰三角形
5.等腰三角形的两边分别为4cm和2cm,则这个三角形的周长是( )。
A.10cm B.8cm C.8cm或10cm
6.下面哪组中的三条线段可以围成一个三角形( )。
A. B. C.
7.一个等腰三角形的两条边分别是5厘米、10厘米,它的周长是( )厘米。
A.20 B.25 C.20或25
8.小明要用三根木条钉成一个三角形,他已经选好了11厘米、5厘米长的两根木条,第三根木条的长度最短是( )厘米。(取整厘米数)
A.6 B.7 C.11
二、填空题
9.一个等腰三角形的底角是30°,它的顶角是( )°,按角分这是个( )三角形。
10.求角的度数,已知∠1=35°,那么∠2=( )°,∠3=( )°,∠4=( )°。
11.在等腰三角形中,当底角是43°的时候,那么它的顶角是( )°,按角来分它属于( )三角形。
12.如图中有( )个三角形,( )个平行四边形,( )个梯形。
13.一个等腰三角形,它的一条边长是5厘米,另一条边长是6厘米,这个三角形的周长是( )厘米。一个等边三角形的周长是24厘米,它一条边的长是( )厘米。
14.小明做一个等腰三角形框架,两条边长分别是5厘米和10厘米,这个框架至少需要( )厘米的木条。
15.小华用小棒拼一个三角形,其中2根的长分别是6厘米、3厘米,第三根最长是( )厘米。(填写整厘米数)
16.一个等腰三角形,它的底角是30°,顶角是( )°。如果它的周长是8米,一条腰长m米,它的底长( )米。
三、判断题
17.连接相对顶点的弧线把平行四边形分成了两部分,两部分的周长一样。( )
18.小明说他做了一个等腰三角形,这个等腰三角形的一个底角92°。( )
19.小明说他从4根分别是4厘米、5厘米、6厘米、8厘米的小棒中,任意选出3根,一定能围成一个三角形。( )
20.任何两个等底等高的梯形,都一定能拼成一个平行四边形。( )
21.有三条线段分别长3cm、7cm、10cm,它们能组成一个三角形。( )
四、图形计算
22.如图所示,求∠1,∠2,∠3各是多少度?
五、解答题
23.明明用一根长18厘米的铁丝围成了一个三角形,这个三角形的边长分别是几厘米?(每段都是整厘米)请把你想到的数据列举2-3组写在下面。
24.从数学的角度观察方格中的两个图形,它们有哪些共同的特点?请至少写出2条。
25.一个三角形的3条边都是整米数。第一条边长是15米,第二条边长是7米,第三条边长可能是多少米?
26.用一根长18.6厘米的铁丝正好围成一个等腰梯形。梯形的上底是2.6厘米,下底是4厘米,它的一条腰长多少厘米?
27.用一根绳子恰好可以围成一个边长是12分米的等边三角形,如果用这根绳子围成底边长是14分米的等腰三角形,这个三角形的一条腰长是多少分米?
28.用一根21.9厘米长的铁丝正好围成一个等腰梯形。梯形的上底是3.4厘米,下底是6.5厘米,它的一条腰长多少厘米?
29.用绳子围一个等腰梯形,腰长为15厘米,上底为24厘米,下底为26厘米。围成这个等腰梯形需要多长的绳子?
30.用一根长26厘米的铁丝圈一个等腰三角形,测的一条边的长度为10厘米,另外两边分别长多少厘米?
参考答案:
1.A
【分析】根据三角形任意两边之和大于第三边,进行分析。
【详解】A.4+5>6,可以;
B.4+6=10,不可以;
C.4+6<12,不可以。
故答案为:A
【点睛】关键是掌握三角形三边之间的关系。
2.C
【分析】三角形内角和180度,假设有两个角都是50度,让一个角尽可能的大,再根据三角形分类标准确定三角形类型即可。
【详解】180-50-50=80(度)
这个三角形一定是锐角三角形。
故答案为:C
【点睛】关键是掌握三角形内角和以及三角形按角分类标准。
3.B
【分析】根据三角形三边关系:三角形的任意两边之和大于第三边;进行分析即可得出结论。
【详解】A.a+b>c,两边之和大于第三边,符合三角形三边关系,本选项正确;
B.a+b<c,两边之和小于第三边,不符合三角形三边关系,所以本选项不正确;
C.a+c>b,两边之和大于第三边,符合三角形三边关系,本选项正确。
故答案为:B
【点睛】熟练掌握三角形三边关系,是解答此题的关键。
4.B
【分析】先对每个选项中的说法进行分析并判断,然后选择正确的一项即可。
A.从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,依此判断;
B.只有一组对边平行的四边形叫做梯形,依此判断;
C.等腰三角形的两腰相等,三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此判断即可。
【详解】A.平行四边形有无数条高,即原说法正确;
B.只有一组对边平行的四边形是梯形,即原说法错误;
C.2dm+2dm>3dm,3dm-2dm<2dm,2dm=2dm,即用长度分别是2dm、2dm、3dm的三根小棒可以围成一个等腰三角形,即原说法正确。
故答案为:B
【点睛】此题考查的是平行四边形的高,梯形的特点,以及三角形3条边的关系,应熟练掌握。
5.A
【分析】根据等腰三角形的性质,当腰长是2cm时,则三角形的三边是2cm,2cm,4cm,2cm+2cm=4cm不满足三角形的三边关系;当腰长是4cm时,三角形的三边是4cm,4cm,2cm,4cm+2cm=6cm>4cm,能构成三角形,据此求出三角形的周长即可。
【详解】根据等腰三角形的性质得,三角形的腰长是4cm,底是2cm,
周长:
故答案为:A
【点睛】本题考查了等腰三角形的性质和三角形的三边关系。
6.B
【分析】判断三角形能否构成,关键是看三条线段是否满足:任意两边之和是否大于第三边,但通常不需要一一验证,其简便方法是将较短两边之和与较长边比较。
【详解】A.2+6<10,不能围成三角形;
B.3+4>5,能围成三角形;
C.8+8=16,不能围成三角形。
故答案为:B
【点睛】本题主要考查三角形的三边关系:三角形任意两边之和大于第三边。
7.B
【分析】在三角形中,两边之和大于第三边,所以这个等腰三角形的腰为10厘米,那么把三角形的三条边相加即可得到这个等腰三角形的周长,据此列式解答。
【详解】因为5+5=10,
所以5厘米的边只能是底。
它的周长是:10+10+5
=20+5
=25(厘米)
故答案为:B
【点睛】此题主要考查三角形的三边关系以及三角形周长的计算方法。
8.B
【分析】任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,此题依此选择即可。
【详解】1-5=6(厘米);11+5=16(厘米);
6厘米<第三边的长度<16厘米
6+1=7(厘米)
因此第三根木条的长度最短是7厘米。
故答案为:B
【点睛】熟练掌握三角形三条边之间的关系是解答本题的关键。
9. 120 钝角
【分析】等腰三角形的两腰相等,两个底角都相等,三角形的内角和为180°,因此用180°减去2个30°即可得到顶角的度数,依此计算并根据三角形的分类标准填空,有一个角是钝角的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,三个角都是锐角的三角形是锐角三角形。
【详解】30°+30°=60°
180°-60°=120°
120°>90°,因此按角分这是一个钝角三角形。
一个等腰三角形的底角是30°,它的顶角是(120)°,按角分这是个(钝角)三角形。
【点睛】此题考查的是三角形的分类标准,等腰三角形的特点,以及三角形的内角和,应熟练掌握。
10. 35 55 55
【分析】长方形中有4个直角,直角是90°,因此用90°减∠1的度数即可计算出∠3的度数;
三角形的内角和是180°,因此用180°减去90°,再减去∠3的度数即可得到∠2的度数;
用90°减∠2的度数即可计算出∠4的度数;依此计算。
【详解】∠3=90°-35°=55°;
∠2=180°-90°-55°=90°-55°=35°;
∠4=90°-35°=55°。
【点睛】解答此题的关键是要熟练掌握长方形的特点,以及熟记三角形的内角和。
11. 94 钝角
【分析】三个角都是锐角的三角形,叫锐角三角形;有一个角是直角的三角形,叫直角三角形;有一个角是钝角的三角形,叫钝角三角形;等腰三角形两底角相等,用三角形的内角和减去两个底角的度数,就是顶角的度数,然后按照角的分类方法确定它是什么三角形即可。
【详解】180°-43°-43°
=137°-43°
=94°
在等腰三角形中,当底角是43°的时候,那么它的顶角是(94)°,按角来分它属于(钝角)三角形。
【点睛】熟悉等腰三角形的特征是解答此题的关键。
12. 5 2 6
【分析】三条边围成的图形是三角形,平行四边形的两组对边分别平行,梯形的一组对边平行,另一组对边不平行。根据图形的特点进行解答。
【详解】根据分析可知,
图中有5个三角形,2个平行四边形,6个梯形。
【点睛】数梯形个数时易错,注意按一定顺序不重不漏地数是解题的关键。
13. 16##17 8
【分析】根据等腰三角形的两条腰相等,先求出另一条边是多少厘米,然后即可求出等腰三角形的周长;等边三角形的三条边长都相等,用周长除以3即可求出边长是多少厘米。
【详解】两条腰都是5厘米时,
周长:5+5+6
=10+6
=16(厘米)
两条腰都是6厘米时,
周长:6+6+5
=12+5
=17(厘米)
24÷3=8(厘米)
【点睛】此题主要考查对等腰三角形和等边三角形的认识。
14.25
【分析】等腰三角形的两腰相等,三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边;依此计算出第三条边最短的长度,然后再计算出这个等腰三角形的周长即可。
【详解】当5厘米为腰长时,5+5=10(厘米),此种情况不满足;
当10厘米为腰长时,5厘米+10厘米>10厘米;10厘米-5厘米<10厘米
10+10+5=25(厘米)
【点睛】此题考查的是三角形周长的计算,等腰三角形的特点,以及三角形3条边的关系,应熟练掌握。
15.8
【分析】根据三角形三边关系:任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,由此计算并解答即可。
【详解】6-3<第三边<6+3,
所以:3<第三边<9,
即第三边的取值在3~9厘米(不包括3厘米和9厘米),
因为三根小棒都是整厘米数,所以第三根小棒最短是:3+1=4(厘米)
最长是:9-1=8(厘米)。
【点睛】此题关键是根据三角形三边关系进行分析、解答。
16. 120 8-2m
【分析】因为三角形的内角和是180°,该三角形是等腰三角形,它的底角是30°,因为等腰三角形两个底角相等,顶角是180°-30°-30°=120°;
求等腰三角形的底边长度,用等腰三角形的周长减去两条腰长即可解答。
【详解】180°-30°-30°
=150°-30°
=120°
8-m-m=(8-2m)米
一个等腰三角形,它的底角是30°,顶角是120°。如果它的周长是8米,一条腰长m米,它的底长8-2m米。
【点睛】此题考查了三角形的内角和,用到的知识点:等腰三角形两底角相等,两腰长相等。
17.√
【分析】根据平行四边形的性质,平行四边形的对边相等,分别看分成的两部分的周长都有哪几部分围成,据此判断。
【详解】平行四边形对边相等,分成两部分的周长分别由平行四边形的一组对边和一条共同的弧围成,所以两部分的周长一样。
故答案为:√
【点睛】解答本题的关键是熟练掌握平行四边形的性质和周长的意义。
18.×
【分析】等腰三角形的两个底角度数相等;三角形的内角和等于180°,据此判断即可。
【详解】两个底角的度数和是92°×2=184°,与三角形的内角和等于180°矛盾。所以原题干说法错误。
故答案为:×
【点睛】本题考查三角形的内角和,明确等腰三角形的两个底角度数相等是解题的关键。
19.√
【分析】根据三角形三边关系:任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,进行解答。
【详解】如:4+5=9(厘米)>8厘米,
所以小明说他从4根分别是4厘米、5厘米、6厘米、8厘米的小棒中,任意选出3根,一定能围成一个三角形,此说法正确。
故答案为:√
【点睛】本题考查了三角形三边关系的灵活应用。
20.×
【分析】两个完全一样的梯形能拼成平行四边形,两个等底等高的梯形在形状完全一样时,可拼成平行四边形。据此解答。
【详解】两个完全相同的梯形才能拼成一个平行四边形;当两个梯形等底等高时,由于梯形的面积=(上底+下底)×高÷2;题干不能确定两个梯形的形状是完全相同的,故不一定能拼成一个平行四边形。
故答案为:×
【点睛】本题主要考查了梯形和平行四边形的关系。要明确两个完全相同的梯形才能拼成一个平行四边形。
21.×
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】3+7=10
则长3cm、7cm、10cm的三条线段不能组成一个三角形。
故答案为:×。
【点睛】本题考查三角形的三边关系,解题时只需要判断较短的两条边的长度和与最长的那条边的长度之间的大小关系即可。
22.∠1=118°,∠2=126°,∠3=116°
【分析】三角形的内角和是180度,则∠3的邻补角=180°-54°-62°=64°,再根据平角等于180°,求出∠1、∠2、∠3各是多少度即可。
【详解】180°-54°-62°
=126°-62°
=64°
∠1=180°-62°=118°
∠2=180°-54°=126°
∠3=180°-64°=116°
答:∠1=118°,∠2=126°,∠3=116°。
23.8厘米、6厘米、4厘米;或5厘米、6厘米、7厘米;或8厘米、5厘米、5厘米;(答案不唯一)
【分析】根据题意可知,三角形的周长是18厘米;三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此进行解答即可。
【详解】假设三角形的两边分别为8厘米、6厘米,则第三边为:18-8-6=4(厘米)
6厘米+4厘米>8厘米,8厘米-4厘米<6厘米,因此这个三角形的边长分别是8厘米、6厘米、4厘米;
假设三角形的两边分别为5厘米、6厘米,则第三边为:18-5-6=7(厘米)
6厘米+5厘米>7厘米,7厘米-6厘米<6厘米,因此这个三角形的边长分别是5厘米、6厘米、7厘米;
假设三角形的两边分别为8厘米、5厘米,则第三边为:18-5-8=5(厘米)
5厘米+5厘米>8厘米,8厘米-5厘米<5厘米,因此这个三角形的边长分别是8厘米、5厘米、5厘米。
答:这个三角形的边长分别是8厘米、6厘米、4厘米;或5厘米、6厘米、7厘米;或8厘米、5厘米、5厘米。
【点睛】此题考查的是三角形的周长,以及三角形三条边之间的关系,应熟练掌握。
24.见详解
【分析】两组对边分别平行的四边形叫做平行四边形;只有一组对边平行的四边形叫做梯形;
平行四边形和梯形共同的特点是:都是由四条线段围成的图形,所以都是四边形;至少有一组对边平行;任意一个四边形的内角和都是360度,所以它们四个内角的和都是360度;
不同点是:平行四边形的两组对边平行且相等,梯形的上底和下底只平行不相等,两条腰不平行也不一定相等。
【详解】平行四边形和梯形的共同特点:
(1)它们都是四边形;
(2)它们内角和都是360度。(答案不唯一)
【点睛】熟练掌握梯形和平行四边形的特点是解答此题的关键。
25.9米;10米;11米;12米;13米;14米;15米;16米;17米;18米;19米;20米;21米
【分析】根据三角形的特征,三角形任意两边的和大于第三边,任意两边的差小于第三边,据此解答。
【详解】15+7=22(米)
15-7=8(米)
所以8米<三角形的第三边<22米
答:第三条边长可能是9米、10米、11米、12米、13米、14米、15米、16米、17米、18米、19米、20米、21米。
【点睛】此题主要考查对三角形的特征的认识。
26.3厘米
【分析】用这根铁丝围成一个等腰梯形,这根铁丝的长度等于等腰梯形的周长。等腰梯形的两条腰相等,则等腰梯形的腰长=(周长-上底-下底)÷2,代入数据计算即可。
【详解】(18.6-2.6-4)÷2
=12÷4
=3(厘米)
答:它的一条腰长3厘米。
【点睛】本题关键是熟记等腰梯形周长的公式:等腰梯形的周长=上底+下底+2×腰。
27.11分米
【分析】两个三角形的周长相等,等边三角形的边长乘3等于等边三角形的周长,减去14分米等于等腰三角形两条腰的长度和,再除以2即等于一条腰的长度。
【详解】(12×3-14)÷2
=(36-14)÷2
=22÷2
=11(分米)
答:这个三角形的一条腰长是11分米。
【点睛】本题主要考查学生对三角形的周长和三角形分类知识的掌握。
28.6厘米
【分析】根据等腰图形的特征,梯形的两条腰的长度相等,用一根21.9厘米长的铁丝正好围成一个等腰梯形,也就是这个梯形的周长是21.9厘米,用梯形的周长减去上下底的长度就是两条腰的长度和,用两条腰的长度和除以2即可求出一条腰的长度。
【详解】(21.9-3.4-6.5)÷2
=12÷2
=6(厘米)
答:它的一条腰长6厘米。
【点睛】此题主要考查梯形周长公式的灵活运用,关键是熟记公式。
29.80厘米
【分析】根据等腰梯形的周长=两条腰的长度+上底+下底,据此解答即可。
【详解】
(厘米)
答:围成这个等腰梯形需要80厘米长的绳子。
【点睛】此题主要考查梯形周长公式的灵活运用,关键是明确等腰梯形的两条腰相等。
30.10厘米和6厘米,或者均为8厘米
【分析】当10厘米是腰长时,用26厘米减去两腰的长度,可求出底的长度;当10厘米是底长时,用26厘米减去底的长度,再将差除以2,可求出腰的长度。据此解题。
【详解】①26-2×10
=26-20
=6(厘米)
②(26-10)÷2
=16÷2
=8(厘米)
答:第一种可能,另外两边的长度为10厘米和6厘米;第二种可能,另外两边的长度均为8厘米。
【点睛】本题考查了等腰三角形,两腰相等的三角形是等腰三角形。
