【解析版】【2014菏泽市一模】山东省菏泽市2014届高三3月模拟考试 数学(文)试题
文档属性
| 名称 | 【解析版】【2014菏泽市一模】山东省菏泽市2014届高三3月模拟考试 数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 681.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-20 08:02:23 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
( http: / / www.21cnjy.com )
第Ⅰ卷(共50分)
一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.设集合 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )
2.已知复数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 ( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B.z的实部为1 C.z的虚部为﹣1 D.z的共轭复数为1+i
( http: / / www.21cnjy.com )
3.下列命题中的真命题是 ( )
A.对于实数、b、c,若,则
B. x2>1是x>1的充分而不必要条件
C. ,使得成立
D.,成立
( http: / / www.21cnjy.com )
4.某几何体的三视图如图1所示,且该几何体的体积是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则正视图中的的值是 ( )
A. 2 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. 3
( http: / / www.21cnjy.com )
【答案】C
【解析】
试题分析:解:由三视图可知,该几何体是底面上底为1,下底为2,高为2的直角梯形的四棱锥,且棱锥的高为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , 底面积为21cnjy.com
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
故选C.
考点:1、空间几何体的三视图;2、棱锥的体积.
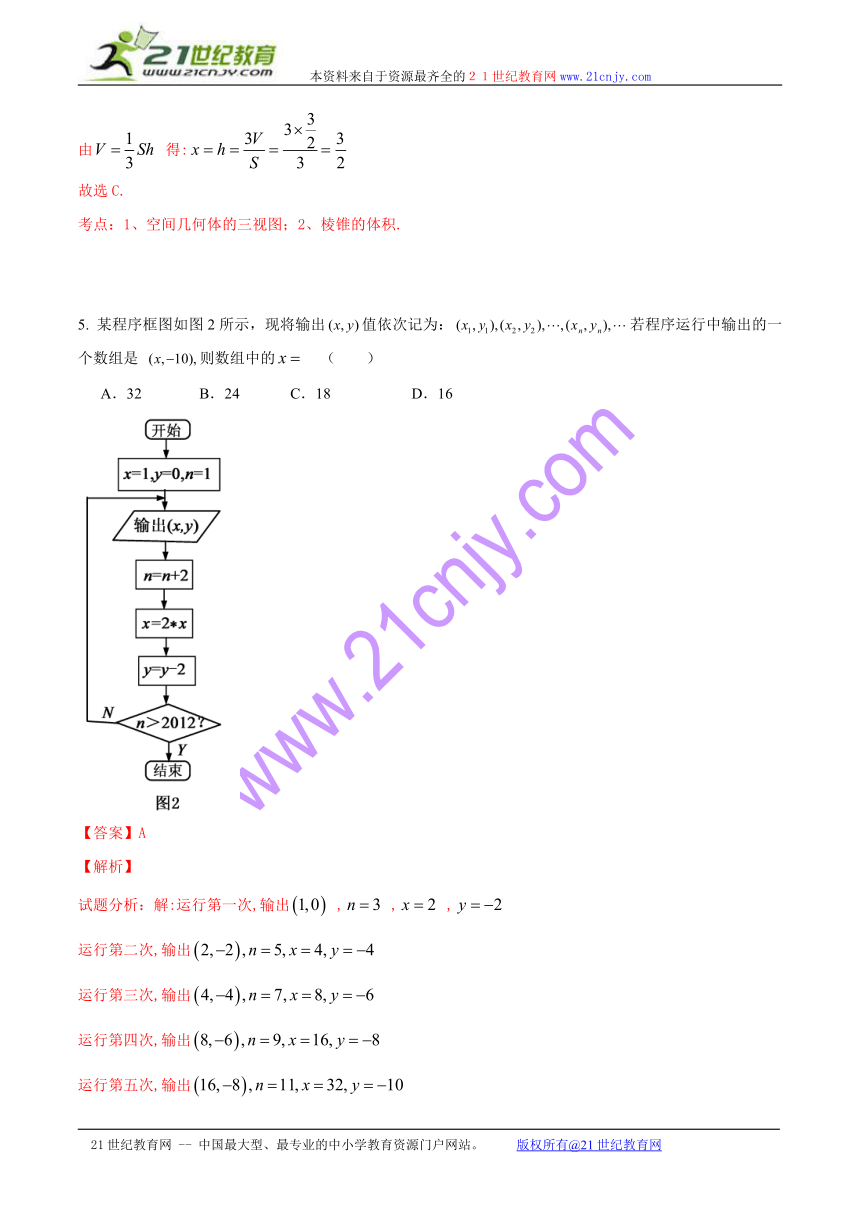
5. 某程序框图如图2所示,现将输出值依次记为:若程序运行中输出的一个数组是 则数组中的 ( )www-2-1-cnjy-com
A.32 B.24 C.18 D.16
( http: / / www.21cnjy.com )
【答案】A
【解析】
试题分析:解:运行第一次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
运行第二次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
运行第三次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
运行第四次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
运行第五次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
运行第六次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
所以选A.
考点:循环结构.
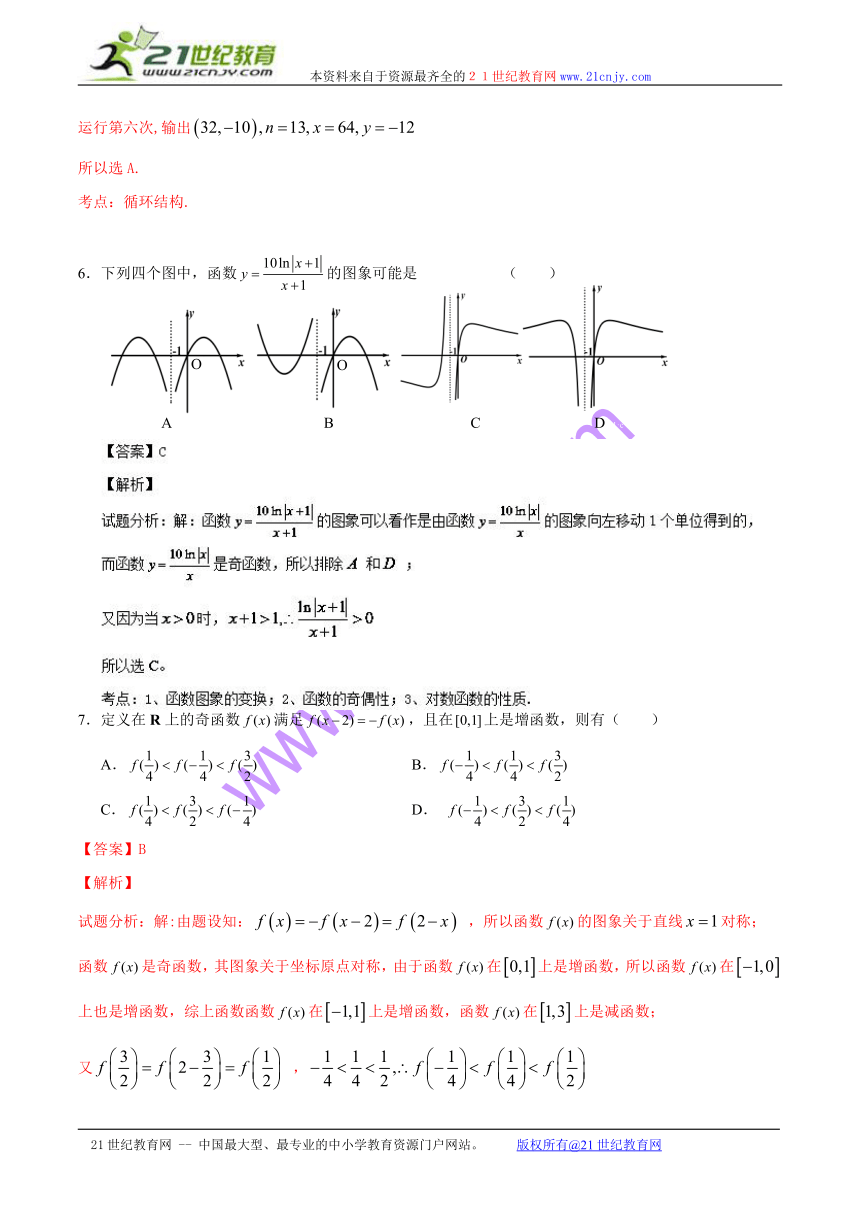
6.下列四个图中,函数的图象可能是 ( )
A B C D2·1·c·n·j·y
( http: / / www.21cnjy.com )
7.定义在R上的奇函数满足,且在上是增函数,则有( )
A. B.
C. D.
【答案】B
【解析】
试题分析:解:由题设知: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以函数的图象关于直线对称;
函数是奇函数,其图象关于坐标原点对称,由于函数在上是增函数,所以函数在上也是增函数,综上函数函数在上是增函数,函数在上是减函数;
又 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
所以,答案应选B.
考点:函数的奇偶性及其与单调性的关系;
8.为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表: 21世纪教育网版权所有
做不到“光盘” 能做到“光盘”
男 45 10
女 30 15
P(K2k) 0.10 0.05 0. 025
k 2.706 3.841 5.024
附:
参照附表,得到的正确结论是 ( )
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”
( http: / / www.21cnjy.com )
9.已知函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若a、b、c互不相等,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则a+b+c的取值范围是 ( )【来源:21·世纪·教育·网】
A.(1,2014) B.(1,2015) C.(2,2015) D.[2,2015]
( http: / / www.21cnjy.com )
10.已知抛物线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的准线过双曲线的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则双曲线的离心率为 ( )www.21-cn-jy.com
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B.4 C.3 D.2
【答案】D
【解析】
试题分析:解:抛物线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的准线方程为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由题意知,双曲线的左焦点坐标为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
且,因为△AOB的面积为,所以,,即: HYPERLINK "http://www.21cnjy.com"
所以,,解得:,
故应选D.
考点:1、抛物线的标准方程;2、双曲线的标准方程及简单几何性质.
第Ⅱ卷(共100分)
二、填空题(每题5分,满分25分,将答案填在答题纸上)
11.设,若f (x)在x=1处的切线与直线垂直,则实数a 的值为 .
( http: / / www.21cnjy.com )
12.设关于x,y的不等式组表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是 . 21*cnjy*com
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
13.在△ABC中,内角A、B、C的对边长分别为a、b、c,已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
则b= .
( http: / / www.21cnjy.com )
14.如图,A是半径为5的圆O上的一个定点,单位向量 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在A点处与圆O相切,点P是圆O上的一个动点,且点P与点A不重合,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 · HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围是 . 【出处:21教育名师】
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
15.函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的定义域为A,若且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时总有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则称
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为单函数.例如,函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是单函数.下列命题:
①函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是单函数; ②函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是单函数;
③若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为单函数, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
④若函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在定义域内某个区间D上具有单调性,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 一定是单函数.
其中真命题是 (写出所有真命题的编号).
( http: / / www.21cnjy.com )
三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分12分)
已知函数()的最小正周期为.
(Ⅰ)求函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的单调增区间;
(Ⅱ)将函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图象向左平移个单位,再向上平移1个单位,得到函数的图象;若在上至少含有10个零点,求b的最小值.2-1-c-n-j-y
【答案】(Ⅰ)(Ⅱ)
【解析】
试题分析:(Ⅰ)由 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
根据函数 的周期 ,可得 ,从而确定的解析式,再根据正弦函数的单调性求出 的单调区间;
Ⅱ) HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" ,选求出函数在长度为一个周期的区间 内的零点,再根据函数的周期性求出原点右侧第十个零点,从而确定 的取值范围.【来源:21cnj*y.co*m】
试题解析:
(Ⅰ)由题意得: HYPERLINK "http://www.21cnjy.com"
( http: / / www.21cnjy.com )
17. (本小题满分12分)如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.【版权所有:21教育】
(Ⅰ)求证: EC⊥CD ;
(Ⅱ)求证:AG∥平面BDE;
(III)求:几何体EG-ABCD的体积.
( http: / / www.21cnjy.com )
【答案】(1)证明过程详见解析;(2)证明过程详见解析;(III)
【解析】
试题分析:(Ⅰ)要证 ,只要证平面;而由题设平面平面且 ,所以平面,结论得证;
( http: / / www.21cnjy.com )
(Ⅰ)证明:由平面ABCD⊥平面BCEG,
平面ABCD∩平面BCEG=BC, 平面BCEG,
EC⊥平面ABCD,…………3分
又CD平面BCDA, 故 EC⊥CD…………4分
(Ⅱ)证明:在平面BCDG中,过G作GN⊥CE交BE于M,连
DM,则由已知知;MG=MN,MN∥BC∥DA,且
MG∥AD,MG=AD, 故四边形ADMG为平行四边形,
AG∥DM……………6分
∵DM平面BDE,AG平面BDE, AG∥平面BDE…………………………8分
(III)解: …………………… 10分
…………………………………………12分
考点:1、直线与平面垂直、平行的判定与性质;2、空间几何体的体积.
18.(本小题满分12分)
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
重量段 [80,85) [85,90) [90,95) [95,100]
件数 5 a 15 b
规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有“A”型2件
(Ⅰ)从该批电器中任选1件,求其为“B”型的概率;
(Ⅱ)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率. ( http: / / www.21cnjy.com )
其中恰有1件为”A”型的情况有ac,ad,ae,bc,bd,be,共6种.………… 10分
所以.所以从重量在[80,85)的5件电器中,任选2件电器,其中恰有1件为”A”型的概率为. …………………………………………………………………………12分21·世纪*教育网
考点:古典概型.
19.(本小题满分12分)
已知数列{an}, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,记 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若对于任意 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,A(n),B(n),C(n)成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{|an|}的前n项和.
试题解析: ( http: / / www.21cnjy.com )
解:(Ⅰ)根据题意A(n), B(n), C(n)成等差数列, ∴A(n)+ C(n)=2 B(n); ...................2分
整理得 ( http: / / www.21cnjy.com ) ,
∴数列{an}是首项为 ( http: / / www.21cnjy.com ),公差为3的等差数列. …………………………………………4分
∴ ( http: / / www.21cnjy.com );.....................……………………………………………….....6分
(Ⅱ) ( http: / / www.21cnjy.com ) , 记数列 ( http: / / www.21cnjy.com )的前n项和为Sn.
当 ( http: / / www.21cnjy.com )时, ( http: / / www.21cnjy.com ) ;…………………………………9分
当 ( http: / / www.21cnjy.com )时, ( http: / / www.21cnjy.com ) ;…………………….11分
综上,. …………………………………………..12分
考点:1、等差数列的通项公式与前 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 项和公式;2、等差中项的性质.
20.(本小题满分13分)
已知关于x的函数
(Ⅰ)当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,求函数的极值;
(Ⅱ)若函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 没有零点,求实数a取值范围. ( http: / / www.21cnjy.com )
当时,,的情况如下表:
2
0
↘ 极小值 ↗
所以,当时,函数的极小值为. ……………………………6分
(Ⅱ). ---7分
①当时,的情况如下表:
2
0
↘ 极小值 ↗
( http: / / www.21cnjy.com )
(或:当时,
当时,令即
由于令
得,即时,即时存在零点.)
综上所述,所求实数a的取值范围是.………………………………13分
考点:1、导数的求法;2、利用导数研究函数的单调性与最值;3、分类讨论的思想.
21.(本小题满分14分)如图;.已知椭圆C: 的离心率为,以椭圆的左顶点T为圆心作圆T:设圆T与椭圆C交于点M、N.21教育网
(Ⅰ)求椭圆C的方程;
(Ⅱ)求的最小值,并求此时圆T的方程;
(Ⅲ)设点P是椭圆C 上异于M,N的任意一点,且直线MP,NP分别与轴交于点R,S,O为坐标原点。求证:为定值.21·cn·jy·com
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )(Ⅲ)设点,利用点分别是直线 与轴的交点,把 用表示,
而,结合点都在椭圆上,将表达式化简即可.
试题解析:
解:(I)由题意知解之得;,由得b=1,
( http: / / www.21cnjy.com )(III)设,则直线MP的方程为
令,得,同理, 故,……10分
又点M与点P在椭圆上,故 ,
得,
为定值.…………………………………………….14分
考点:1、椭圆的标准方程;2、圆的标准方程序;3、向量的数量积;4直线的方程.
O
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
( http: / / www.21cnjy.com )
第Ⅰ卷(共50分)
一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.设集合 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )
2.已知复数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 ( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B.z的实部为1 C.z的虚部为﹣1 D.z的共轭复数为1+i
( http: / / www.21cnjy.com )
3.下列命题中的真命题是 ( )
A.对于实数、b、c,若,则
B. x2>1是x>1的充分而不必要条件
C. ,使得成立
D.,成立
( http: / / www.21cnjy.com )
4.某几何体的三视图如图1所示,且该几何体的体积是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则正视图中的的值是 ( )
A. 2 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. 3
( http: / / www.21cnjy.com )
【答案】C
【解析】
试题分析:解:由三视图可知,该几何体是底面上底为1,下底为2,高为2的直角梯形的四棱锥,且棱锥的高为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , 底面积为21cnjy.com
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
故选C.
考点:1、空间几何体的三视图;2、棱锥的体积.
5. 某程序框图如图2所示,现将输出值依次记为:若程序运行中输出的一个数组是 则数组中的 ( )www-2-1-cnjy-com
A.32 B.24 C.18 D.16
( http: / / www.21cnjy.com )
【答案】A
【解析】
试题分析:解:运行第一次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
运行第二次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
运行第三次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
运行第四次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
运行第五次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
运行第六次,输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
所以选A.
考点:循环结构.
6.下列四个图中,函数的图象可能是 ( )
A B C D2·1·c·n·j·y
( http: / / www.21cnjy.com )
7.定义在R上的奇函数满足,且在上是增函数,则有( )
A. B.
C. D.
【答案】B
【解析】
试题分析:解:由题设知: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以函数的图象关于直线对称;
函数是奇函数,其图象关于坐标原点对称,由于函数在上是增函数,所以函数在上也是增函数,综上函数函数在上是增函数,函数在上是减函数;
又 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
所以,答案应选B.
考点:函数的奇偶性及其与单调性的关系;
8.为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表: 21世纪教育网版权所有
做不到“光盘” 能做到“光盘”
男 45 10
女 30 15
P(K2k) 0.10 0.05 0. 025
k 2.706 3.841 5.024
附:
参照附表,得到的正确结论是 ( )
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”
( http: / / www.21cnjy.com )
9.已知函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若a、b、c互不相等,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则a+b+c的取值范围是 ( )【来源:21·世纪·教育·网】
A.(1,2014) B.(1,2015) C.(2,2015) D.[2,2015]
( http: / / www.21cnjy.com )
10.已知抛物线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的准线过双曲线的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则双曲线的离心率为 ( )www.21-cn-jy.com
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B.4 C.3 D.2
【答案】D
【解析】
试题分析:解:抛物线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的准线方程为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由题意知,双曲线的左焦点坐标为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
且,因为△AOB的面积为,所以,,即: HYPERLINK "http://www.21cnjy.com"
所以,,解得:,
故应选D.
考点:1、抛物线的标准方程;2、双曲线的标准方程及简单几何性质.
第Ⅱ卷(共100分)
二、填空题(每题5分,满分25分,将答案填在答题纸上)
11.设,若f (x)在x=1处的切线与直线垂直,则实数a 的值为 .
( http: / / www.21cnjy.com )
12.设关于x,y的不等式组表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是 . 21*cnjy*com
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
13.在△ABC中,内角A、B、C的对边长分别为a、b、c,已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
则b= .
( http: / / www.21cnjy.com )
14.如图,A是半径为5的圆O上的一个定点,单位向量 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在A点处与圆O相切,点P是圆O上的一个动点,且点P与点A不重合,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 · HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围是 . 【出处:21教育名师】
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
15.函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的定义域为A,若且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时总有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则称
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为单函数.例如,函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是单函数.下列命题:
①函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是单函数; ②函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是单函数;
③若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为单函数, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
④若函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在定义域内某个区间D上具有单调性,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 一定是单函数.
其中真命题是 (写出所有真命题的编号).
( http: / / www.21cnjy.com )
三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)
16.(本小题满分12分)
已知函数()的最小正周期为.
(Ⅰ)求函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的单调增区间;
(Ⅱ)将函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图象向左平移个单位,再向上平移1个单位,得到函数的图象;若在上至少含有10个零点,求b的最小值.2-1-c-n-j-y
【答案】(Ⅰ)(Ⅱ)
【解析】
试题分析:(Ⅰ)由 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
根据函数 的周期 ,可得 ,从而确定的解析式,再根据正弦函数的单调性求出 的单调区间;
Ⅱ) HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" ,选求出函数在长度为一个周期的区间 内的零点,再根据函数的周期性求出原点右侧第十个零点,从而确定 的取值范围.【来源:21cnj*y.co*m】
试题解析:
(Ⅰ)由题意得: HYPERLINK "http://www.21cnjy.com"
( http: / / www.21cnjy.com )
17. (本小题满分12分)如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.【版权所有:21教育】
(Ⅰ)求证: EC⊥CD ;
(Ⅱ)求证:AG∥平面BDE;
(III)求:几何体EG-ABCD的体积.
( http: / / www.21cnjy.com )
【答案】(1)证明过程详见解析;(2)证明过程详见解析;(III)
【解析】
试题分析:(Ⅰ)要证 ,只要证平面;而由题设平面平面且 ,所以平面,结论得证;
( http: / / www.21cnjy.com )
(Ⅰ)证明:由平面ABCD⊥平面BCEG,
平面ABCD∩平面BCEG=BC, 平面BCEG,
EC⊥平面ABCD,…………3分
又CD平面BCDA, 故 EC⊥CD…………4分
(Ⅱ)证明:在平面BCDG中,过G作GN⊥CE交BE于M,连
DM,则由已知知;MG=MN,MN∥BC∥DA,且
MG∥AD,MG=AD, 故四边形ADMG为平行四边形,
AG∥DM……………6分
∵DM平面BDE,AG平面BDE, AG∥平面BDE…………………………8分
(III)解: …………………… 10分
…………………………………………12分
考点:1、直线与平面垂直、平行的判定与性质;2、空间几何体的体积.
18.(本小题满分12分)
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
重量段 [80,85) [85,90) [90,95) [95,100]
件数 5 a 15 b
规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有“A”型2件
(Ⅰ)从该批电器中任选1件,求其为“B”型的概率;
(Ⅱ)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率. ( http: / / www.21cnjy.com )
其中恰有1件为”A”型的情况有ac,ad,ae,bc,bd,be,共6种.………… 10分
所以.所以从重量在[80,85)的5件电器中,任选2件电器,其中恰有1件为”A”型的概率为. …………………………………………………………………………12分21·世纪*教育网
考点:古典概型.
19.(本小题满分12分)
已知数列{an}, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,记 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若对于任意 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,A(n),B(n),C(n)成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{|an|}的前n项和.
试题解析: ( http: / / www.21cnjy.com )
解:(Ⅰ)根据题意A(n), B(n), C(n)成等差数列, ∴A(n)+ C(n)=2 B(n); ...................2分
整理得 ( http: / / www.21cnjy.com ) ,
∴数列{an}是首项为 ( http: / / www.21cnjy.com ),公差为3的等差数列. …………………………………………4分
∴ ( http: / / www.21cnjy.com );.....................……………………………………………….....6分
(Ⅱ) ( http: / / www.21cnjy.com ) , 记数列 ( http: / / www.21cnjy.com )的前n项和为Sn.
当 ( http: / / www.21cnjy.com )时, ( http: / / www.21cnjy.com ) ;…………………………………9分
当 ( http: / / www.21cnjy.com )时, ( http: / / www.21cnjy.com ) ;…………………….11分
综上,. …………………………………………..12分
考点:1、等差数列的通项公式与前 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 项和公式;2、等差中项的性质.
20.(本小题满分13分)
已知关于x的函数
(Ⅰ)当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,求函数的极值;
(Ⅱ)若函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 没有零点,求实数a取值范围. ( http: / / www.21cnjy.com )
当时,,的情况如下表:
2
0
↘ 极小值 ↗
所以,当时,函数的极小值为. ……………………………6分
(Ⅱ). ---7分
①当时,的情况如下表:
2
0
↘ 极小值 ↗
( http: / / www.21cnjy.com )
(或:当时,
当时,令即
由于令
得,即时,即时存在零点.)
综上所述,所求实数a的取值范围是.………………………………13分
考点:1、导数的求法;2、利用导数研究函数的单调性与最值;3、分类讨论的思想.
21.(本小题满分14分)如图;.已知椭圆C: 的离心率为,以椭圆的左顶点T为圆心作圆T:设圆T与椭圆C交于点M、N.21教育网
(Ⅰ)求椭圆C的方程;
(Ⅱ)求的最小值,并求此时圆T的方程;
(Ⅲ)设点P是椭圆C 上异于M,N的任意一点,且直线MP,NP分别与轴交于点R,S,O为坐标原点。求证:为定值.21·cn·jy·com
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )(Ⅲ)设点,利用点分别是直线 与轴的交点,把 用表示,
而,结合点都在椭圆上,将表达式化简即可.
试题解析:
解:(I)由题意知解之得;,由得b=1,
( http: / / www.21cnjy.com )(III)设,则直线MP的方程为
令,得,同理, 故,……10分
又点M与点P在椭圆上,故 ,
得,
为定值.…………………………………………….14分
考点:1、椭圆的标准方程;2、圆的标准方程序;3、向量的数量积;4直线的方程.
O
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
