2022-2023学年七年级数学下册人教版 5.2.1平行线认识 同步练习 (含答案)
文档属性
| 名称 | 2022-2023学年七年级数学下册人教版 5.2.1平行线认识 同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 250.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 08:07:08 | ||
图片预览



文档简介
5.2.1平行线
(同步练习)
一、单选题
1.下列说法:
①两点之间,直线最短;
②若AC=BC,则点C是线段AB的中点;
③同一平面内过一点有且只有一条直线与已知直线垂直;
④过一点有且只有一条直线与已知直线平行.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
2.给出下列说法:(1)过平面内一点有且只有一条直线与已知直线平行;(2)相等的两个角是对顶角;(3)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;(4)不相交的两条直线叫做平行线;(5)垂直于同一条直线的两条直线平行.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
3.在同一平面内,直线AB与CD相交,AB与EF平行,则CD与EF( )
A.平行 B.相交
C.重合 D.三种情况都有可能
4.下列结论错误的是( )
A.垂直于同一直线的两条直线互相平行
B.两直线平行,同旁内角互补
C.过直线外一点有且只有一条直线与这条直线平行
D.同一平面内,不相交的两条直线叫做平行线
5.下列四种说法:①对顶角相等;②两点之间直线最短;③经过直线外一点有且只有一条直线与已知直线平行;④直线外一点与直线上各点连接的所有线段中,垂线段最短.其中正确的是( )
A.④ B.①④ C.③④ D.①③④
6.下列语句正确的是( )
A.在所有联结两点的线中,直线最短
B.线段AB是点A与点B的距离
C.三条直线两两相交,必定有三个交点
D.在同一平面内,两条不重合的直线,不平行必相交
7.下列说法中正确的是( )
A.两条相交的直线叫做平行线 B.如果a∥b,b∥c,则a不与c平行
C.在直线外一点,只能画出一条直线与已知直线平行 D.两条不平行的射线,在同一平面内一定相交
8.下列说法正确的是( )
A.两点之间,直线最短
B.永不相交的两条直线叫做平行线
C.若AC=BC,则点C为线段AB的中点
D.两点确定一条直线
9.下列结论正确的是 ( )
A.不相交的直线互相平行
B.不相交的线段互相平行
C.不相交的射线互相平行
D.有公共点的两条直线一定不平行
10.同一平面内如果两条直线不重合,那么他们( )
A.平行 B.相交 C.相交或垂直 D.平行或相交
二、填空题
11.规律探究:同一平面内有直线、、,,,若,,,,,按此规律,与的位置关系是______.
12.如果两条直线和第三条直线________,那么这两条直线平行;若a∥b , b∥c,则________.
13.在同一平面内,直线AB与直线CD满足下列条件,则其对应的位置关系是
(1)若直线AB与直线CD没有公共点,则直线AB与直线CD的位置关系为__________;
(2)直线AB与直线CD有且只有一个公共点,则直线AB与直线CD的位置关系为_____.
14.如图所示,能相交的是__________,平行的是__________.
15.如果直线a//b,且直线,则直线c与b的位置关系_______ (“平行”或“垂直”)
三、解答题
16.如图,在6×6的正方形网格中,每个小正方形的边长是1,点M、N、P、Q均为格点(格点是指每个小正方形的顶点),线段MN经过点P.
(1)过点P画线段AB,使得线段AB满足以下两个条件:①AB⊥MN;②;
(2)过点Q画MN的平行线CD,CD与AB相交于点E;
(3)若格点F使得△PFM的面积等于4,则这样的点F共有 个.
17.如图所示的是一幅七巧板的模型图,请你找出图中各对互相平行的直线,并用符号表示出来.
18.如图都是4×4的网格正方形,且每个小正方形边长都为1,请你利用无刻度直尺,按下列要求画图(保留作图痕迹,不写作法).
(1)在图1中,画直线AB∥CD,且AB与CD之间的距离为2.
(2)在图2中,画一个直角三角形,使三角形的顶点都在格点上,且面积为3.
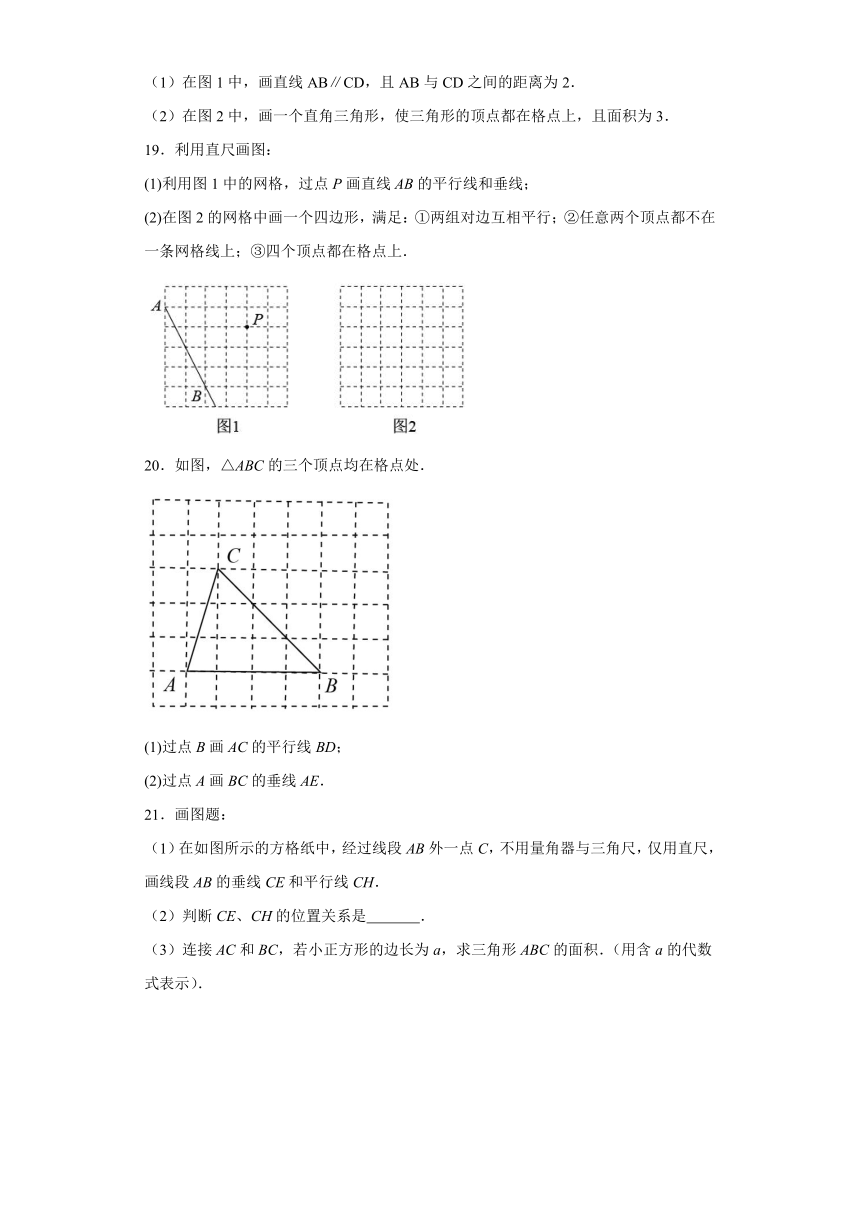
19.利用直尺画图:
(1)利用图1中的网格,过点P画直线AB的平行线和垂线;
(2)在图2的网格中画一个四边形,满足:①两组对边互相平行;②任意两个顶点都不在一条网格线上;③四个顶点都在格点上.
20.如图,△ABC的三个顶点均在格点处.
(1)过点B画AC的平行线BD;
(2)过点A画BC的垂线AE.
21.画图题:
(1)在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线CE和平行线CH.
(2)判断CE、CH的位置关系是 .
(3)连接AC和BC,若小正方形的边长为a,求三角形ABC的面积.(用含a的代数式表示).
参考答案:
1.A2.A3.B4.A5.D6.D7.C8.D9.D10.D
11.互相垂直.
12. 平行 a∥c
13. 平行 ;相交.
14. ③; ⑤.
15.垂直
16.(1)解:作图如下:
(2)解:作图见(1)
(3)如图:
故符合题意的点F有6个.
故答案为:6
17.AD∥BC,AB∥HG∥DC,EF∥BH,EK∥AC.
18.(1)图1中AB、CD为所画.
(2)图2中△ABC为所画.
19.(1)CD∥AB,PQ⊥AB.
(2)四边形ABCD是符合条件的四边形.
20.(1)解:如图,直线BD即为所求作.
(2)如图,直线AE即为所求作.
21.(1)如图,根据正方形的性质,找到点E连接CE即为所求作的AB的垂线,利用对称性找到点H,连接CH即为所求AB的平行线;
(2)∵CE⊥AB,CH∥AB,
∴∠ECH=90°,
∴CH⊥CE
CE、CH的位置关系是CE⊥CH.
故答案为:CE⊥CH;
(3)如图,连接AC和BC,
∵小方格的边长为a,则三角形ABC的面积为
=16a2﹣×(3a)2﹣2××a×4a=a2.
故答案为:a2.
(同步练习)
一、单选题
1.下列说法:
①两点之间,直线最短;
②若AC=BC,则点C是线段AB的中点;
③同一平面内过一点有且只有一条直线与已知直线垂直;
④过一点有且只有一条直线与已知直线平行.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
2.给出下列说法:(1)过平面内一点有且只有一条直线与已知直线平行;(2)相等的两个角是对顶角;(3)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;(4)不相交的两条直线叫做平行线;(5)垂直于同一条直线的两条直线平行.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
3.在同一平面内,直线AB与CD相交,AB与EF平行,则CD与EF( )
A.平行 B.相交
C.重合 D.三种情况都有可能
4.下列结论错误的是( )
A.垂直于同一直线的两条直线互相平行
B.两直线平行,同旁内角互补
C.过直线外一点有且只有一条直线与这条直线平行
D.同一平面内,不相交的两条直线叫做平行线
5.下列四种说法:①对顶角相等;②两点之间直线最短;③经过直线外一点有且只有一条直线与已知直线平行;④直线外一点与直线上各点连接的所有线段中,垂线段最短.其中正确的是( )
A.④ B.①④ C.③④ D.①③④
6.下列语句正确的是( )
A.在所有联结两点的线中,直线最短
B.线段AB是点A与点B的距离
C.三条直线两两相交,必定有三个交点
D.在同一平面内,两条不重合的直线,不平行必相交
7.下列说法中正确的是( )
A.两条相交的直线叫做平行线 B.如果a∥b,b∥c,则a不与c平行
C.在直线外一点,只能画出一条直线与已知直线平行 D.两条不平行的射线,在同一平面内一定相交
8.下列说法正确的是( )
A.两点之间,直线最短
B.永不相交的两条直线叫做平行线
C.若AC=BC,则点C为线段AB的中点
D.两点确定一条直线
9.下列结论正确的是 ( )
A.不相交的直线互相平行
B.不相交的线段互相平行
C.不相交的射线互相平行
D.有公共点的两条直线一定不平行
10.同一平面内如果两条直线不重合,那么他们( )
A.平行 B.相交 C.相交或垂直 D.平行或相交
二、填空题
11.规律探究:同一平面内有直线、、,,,若,,,,,按此规律,与的位置关系是______.
12.如果两条直线和第三条直线________,那么这两条直线平行;若a∥b , b∥c,则________.
13.在同一平面内,直线AB与直线CD满足下列条件,则其对应的位置关系是
(1)若直线AB与直线CD没有公共点,则直线AB与直线CD的位置关系为__________;
(2)直线AB与直线CD有且只有一个公共点,则直线AB与直线CD的位置关系为_____.
14.如图所示,能相交的是__________,平行的是__________.
15.如果直线a//b,且直线,则直线c与b的位置关系_______ (“平行”或“垂直”)
三、解答题
16.如图,在6×6的正方形网格中,每个小正方形的边长是1,点M、N、P、Q均为格点(格点是指每个小正方形的顶点),线段MN经过点P.
(1)过点P画线段AB,使得线段AB满足以下两个条件:①AB⊥MN;②;
(2)过点Q画MN的平行线CD,CD与AB相交于点E;
(3)若格点F使得△PFM的面积等于4,则这样的点F共有 个.
17.如图所示的是一幅七巧板的模型图,请你找出图中各对互相平行的直线,并用符号表示出来.
18.如图都是4×4的网格正方形,且每个小正方形边长都为1,请你利用无刻度直尺,按下列要求画图(保留作图痕迹,不写作法).
(1)在图1中,画直线AB∥CD,且AB与CD之间的距离为2.
(2)在图2中,画一个直角三角形,使三角形的顶点都在格点上,且面积为3.
19.利用直尺画图:
(1)利用图1中的网格,过点P画直线AB的平行线和垂线;
(2)在图2的网格中画一个四边形,满足:①两组对边互相平行;②任意两个顶点都不在一条网格线上;③四个顶点都在格点上.
20.如图,△ABC的三个顶点均在格点处.
(1)过点B画AC的平行线BD;
(2)过点A画BC的垂线AE.
21.画图题:
(1)在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线CE和平行线CH.
(2)判断CE、CH的位置关系是 .
(3)连接AC和BC,若小正方形的边长为a,求三角形ABC的面积.(用含a的代数式表示).
参考答案:
1.A2.A3.B4.A5.D6.D7.C8.D9.D10.D
11.互相垂直.
12. 平行 a∥c
13. 平行 ;相交.
14. ③; ⑤.
15.垂直
16.(1)解:作图如下:
(2)解:作图见(1)
(3)如图:
故符合题意的点F有6个.
故答案为:6
17.AD∥BC,AB∥HG∥DC,EF∥BH,EK∥AC.
18.(1)图1中AB、CD为所画.
(2)图2中△ABC为所画.
19.(1)CD∥AB,PQ⊥AB.
(2)四边形ABCD是符合条件的四边形.
20.(1)解:如图,直线BD即为所求作.
(2)如图,直线AE即为所求作.
21.(1)如图,根据正方形的性质,找到点E连接CE即为所求作的AB的垂线,利用对称性找到点H,连接CH即为所求AB的平行线;
(2)∵CE⊥AB,CH∥AB,
∴∠ECH=90°,
∴CH⊥CE
CE、CH的位置关系是CE⊥CH.
故答案为:CE⊥CH;
(3)如图,连接AC和BC,
∵小方格的边长为a,则三角形ABC的面积为
=16a2﹣×(3a)2﹣2××a×4a=a2.
故答案为:a2.
