2022-2023学年七年级数学下册人教版5.1相交线 同步练习(含答案)
文档属性
| 名称 | 2022-2023学年七年级数学下册人教版5.1相交线 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 303.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 08:08:15 | ||
图片预览

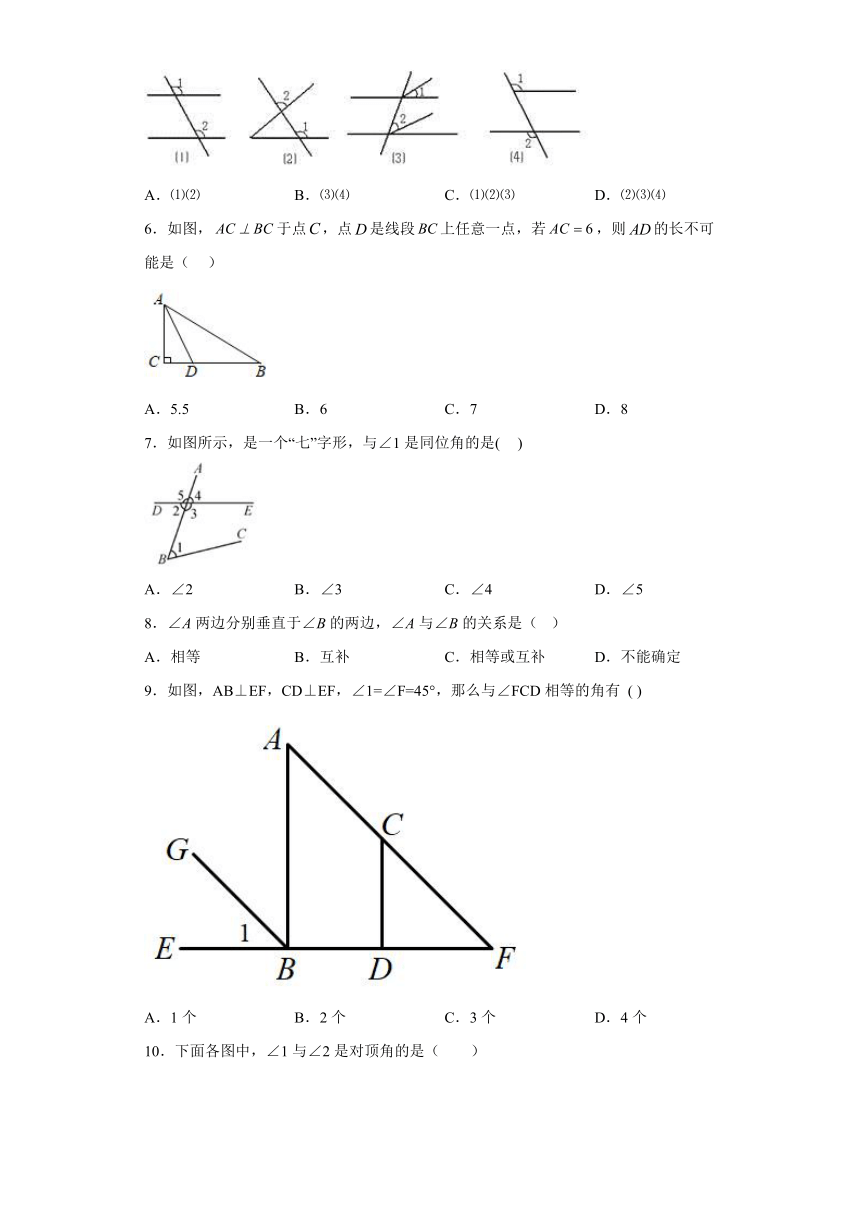
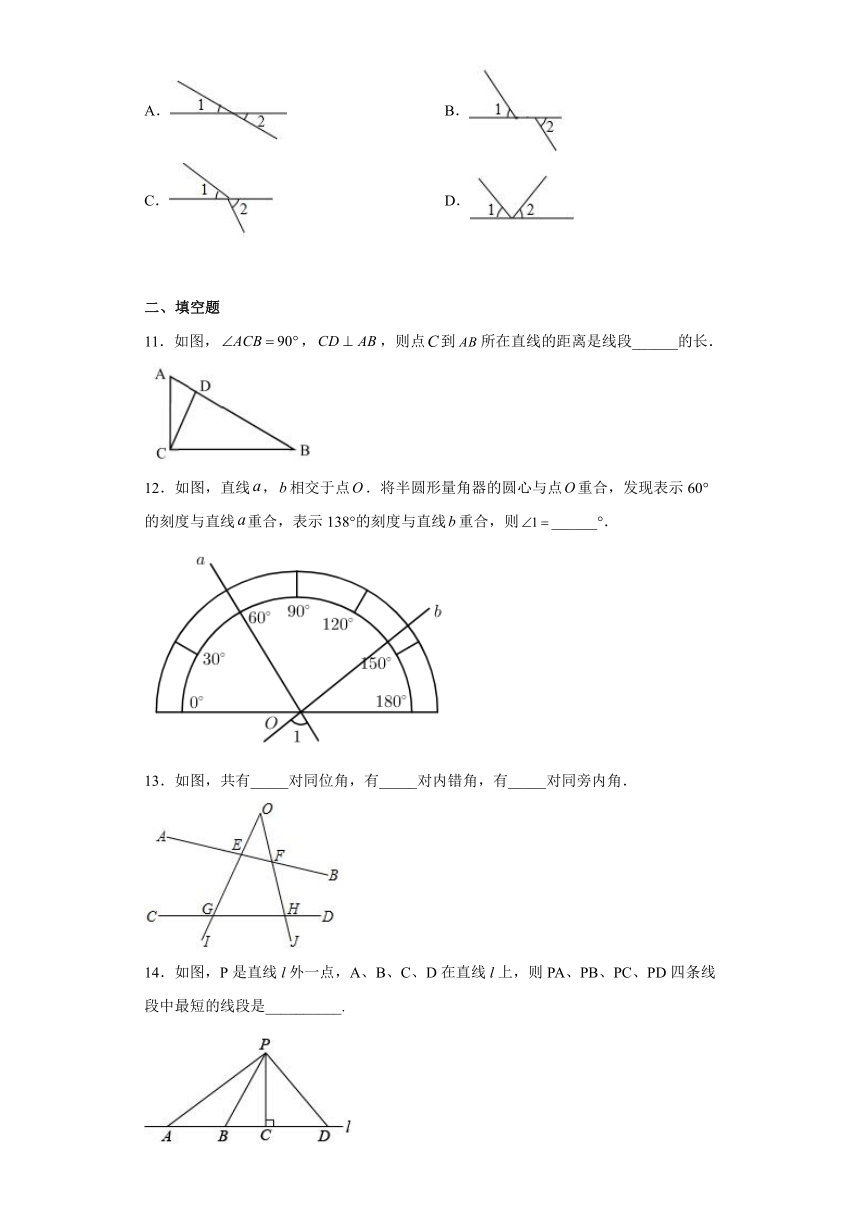
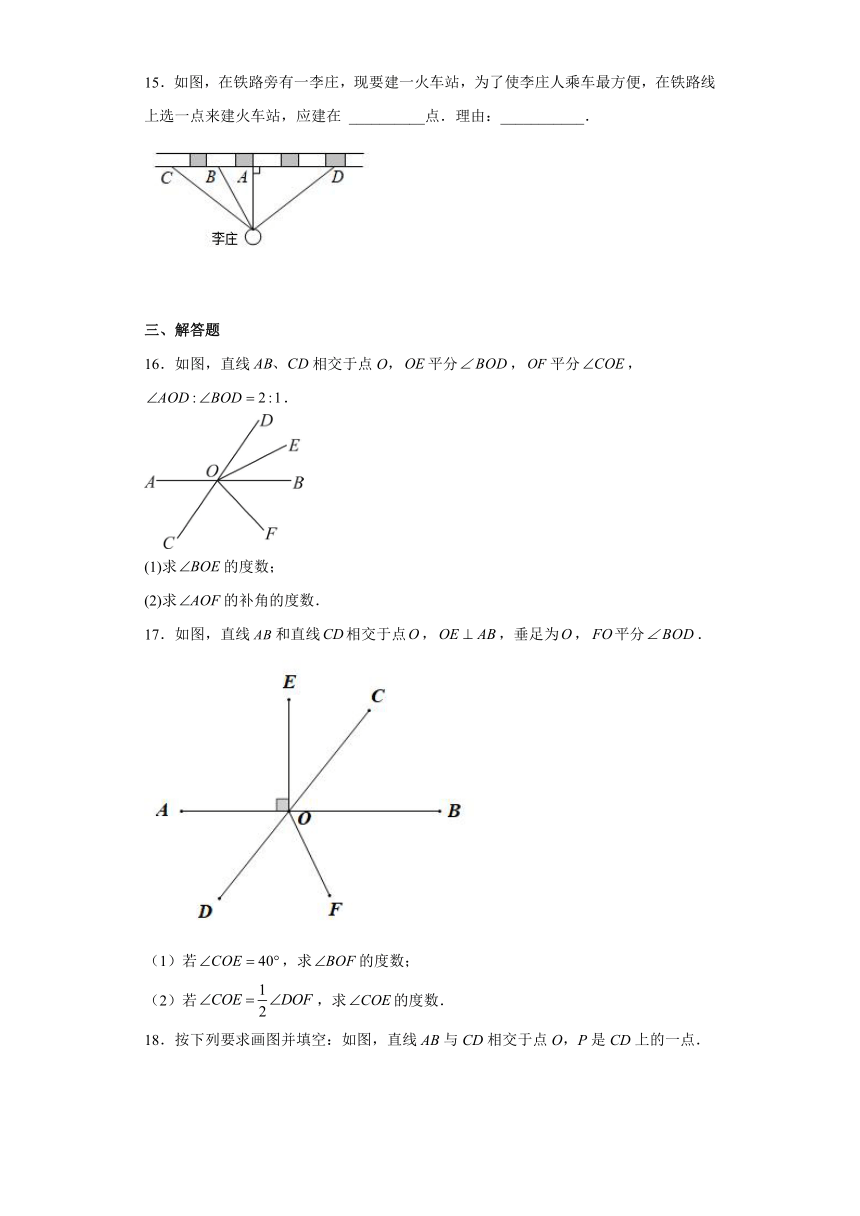
文档简介
5.1相交线
(同步练习)
一、单选题
1.如图,∠1与∠2不是同位角的是( )
A. B.
C. D.
2.如图,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段 D.线段BD是点B到AD的垂线段
3.如图,平行直线AB、CD与相交直线EF、GH相交,图中的同旁内角共有( )
A.4对 B.8对 C.12对 D.16对
4.如图,三条直线相交于点.若,则等于( )
A. B. C. D.
5.下列四幅图中,∠1和∠2是同位角的是( )
A.⑴⑵ B.⑶⑷ C.⑴⑵⑶ D.⑵⑶⑷
6.如图,于点,点是线段上任意一点,若,则的长不可能是( )
A.5.5 B.6 C.7 D.8
7.如图所示,是一个“七”字形,与∠1是同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
8.∠A两边分别垂直于∠B的两边,∠A与∠B的关系是( )
A.相等 B.互补 C.相等或互补 D.不能确定
9.如图,AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠FCD相等的角有 ( )
A.1个 B.2个 C.3个 D.4个
10.下面各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
二、填空题
11.如图,,,则点到所在直线的距离是线段______的长.
12.如图,直线,相交于点.将半圆形量角器的圆心与点重合,发现表示60°的刻度与直线重合,表示138°的刻度与直线重合,则______°.
13.如图,共有_____对同位角,有_____对内错角,有_____对同旁内角.
14.如图,P是直线l外一点,A、B、C、D在直线l上,则PA、PB、PC、PD四条线段中最短的线段是__________.
15.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,在铁路线上选一点来建火车站,应建在 __________点.理由:___________.
三、解答题
16.如图,直线相交于点O,平分,平分,.
(1)求的度数;
(2)求的补角的度数.
17.如图,直线和直线相交于点,,垂足为,平分.
(1)若,求的度数;
(2)若,求的度数.
18.按下列要求画图并填空:如图,直线AB与CD相交于点O,P是CD上的一点.
(1)过点P画出CD的垂线,交直线AB于点E;
(2)过点P画PF⊥AB,垂足为点F;
(3)点O到直线PE的距离是线段 的长;
(4)点P到直线CD的距离为 .
19.如图,直线,相交于点,.
(1)若,则 ;
(2)如果,试说明:⊥.
20.如图,直线、相交于点,平分,垂足为点,且.
(1)如图,求的度数.
(2)在不添加任何辅助线的情况下,请直接写出图中与互余的角.
21.如图,和相交于点,,若.
(1)指出与相等的角,并说明理由;
(2)求,的度数.
参考答案:
1.B2.C3.D4.C5.A6.A7.C8.C9.D10.A
11.
12.78°
13. 20 12 12
14.PC
15. A 垂线段最短
16.(1)
(2)
17.(1);(2);
18.(1)解:如图,直线PE即为所求;
(2)解:如图,直线PF即为所求;
(3)解:点O到直线PE的距离是线段OP的长.
故答案为:OP;
(4)解:由图可知,点P到直线CD的距离为0,
故答案为:0.
19.(1)解:∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=∠AOM=90°,
∵∠1=40°,
∴∠AOC=50°,
故答案为:50°;
(2)解:∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD.
20.(1)
(2)
21.(1),对顶角相等;(2),
(同步练习)
一、单选题
1.如图,∠1与∠2不是同位角的是( )
A. B.
C. D.
2.如图,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段 D.线段BD是点B到AD的垂线段
3.如图,平行直线AB、CD与相交直线EF、GH相交,图中的同旁内角共有( )
A.4对 B.8对 C.12对 D.16对
4.如图,三条直线相交于点.若,则等于( )
A. B. C. D.
5.下列四幅图中,∠1和∠2是同位角的是( )
A.⑴⑵ B.⑶⑷ C.⑴⑵⑶ D.⑵⑶⑷
6.如图,于点,点是线段上任意一点,若,则的长不可能是( )
A.5.5 B.6 C.7 D.8
7.如图所示,是一个“七”字形,与∠1是同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
8.∠A两边分别垂直于∠B的两边,∠A与∠B的关系是( )
A.相等 B.互补 C.相等或互补 D.不能确定
9.如图,AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠FCD相等的角有 ( )
A.1个 B.2个 C.3个 D.4个
10.下面各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
二、填空题
11.如图,,,则点到所在直线的距离是线段______的长.
12.如图,直线,相交于点.将半圆形量角器的圆心与点重合,发现表示60°的刻度与直线重合,表示138°的刻度与直线重合,则______°.
13.如图,共有_____对同位角,有_____对内错角,有_____对同旁内角.
14.如图,P是直线l外一点,A、B、C、D在直线l上,则PA、PB、PC、PD四条线段中最短的线段是__________.
15.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,在铁路线上选一点来建火车站,应建在 __________点.理由:___________.
三、解答题
16.如图,直线相交于点O,平分,平分,.
(1)求的度数;
(2)求的补角的度数.
17.如图,直线和直线相交于点,,垂足为,平分.
(1)若,求的度数;
(2)若,求的度数.
18.按下列要求画图并填空:如图,直线AB与CD相交于点O,P是CD上的一点.
(1)过点P画出CD的垂线,交直线AB于点E;
(2)过点P画PF⊥AB,垂足为点F;
(3)点O到直线PE的距离是线段 的长;
(4)点P到直线CD的距离为 .
19.如图,直线,相交于点,.
(1)若,则 ;
(2)如果,试说明:⊥.
20.如图,直线、相交于点,平分,垂足为点,且.
(1)如图,求的度数.
(2)在不添加任何辅助线的情况下,请直接写出图中与互余的角.
21.如图,和相交于点,,若.
(1)指出与相等的角,并说明理由;
(2)求,的度数.
参考答案:
1.B2.C3.D4.C5.A6.A7.C8.C9.D10.A
11.
12.78°
13. 20 12 12
14.PC
15. A 垂线段最短
16.(1)
(2)
17.(1);(2);
18.(1)解:如图,直线PE即为所求;
(2)解:如图,直线PF即为所求;
(3)解:点O到直线PE的距离是线段OP的长.
故答案为:OP;
(4)解:由图可知,点P到直线CD的距离为0,
故答案为:0.
19.(1)解:∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=∠AOM=90°,
∵∠1=40°,
∴∠AOC=50°,
故答案为:50°;
(2)解:∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD.
20.(1)
(2)
21.(1),对顶角相等;(2),
