2022-2023学年七年级数学下册人教版 5.1.2垂线 同步练习(含答案)
文档属性
| 名称 | 2022-2023学年七年级数学下册人教版 5.1.2垂线 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 485.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 00:00:00 | ||
图片预览



文档简介
5.1.2垂线
(同步练习)
一、单选题
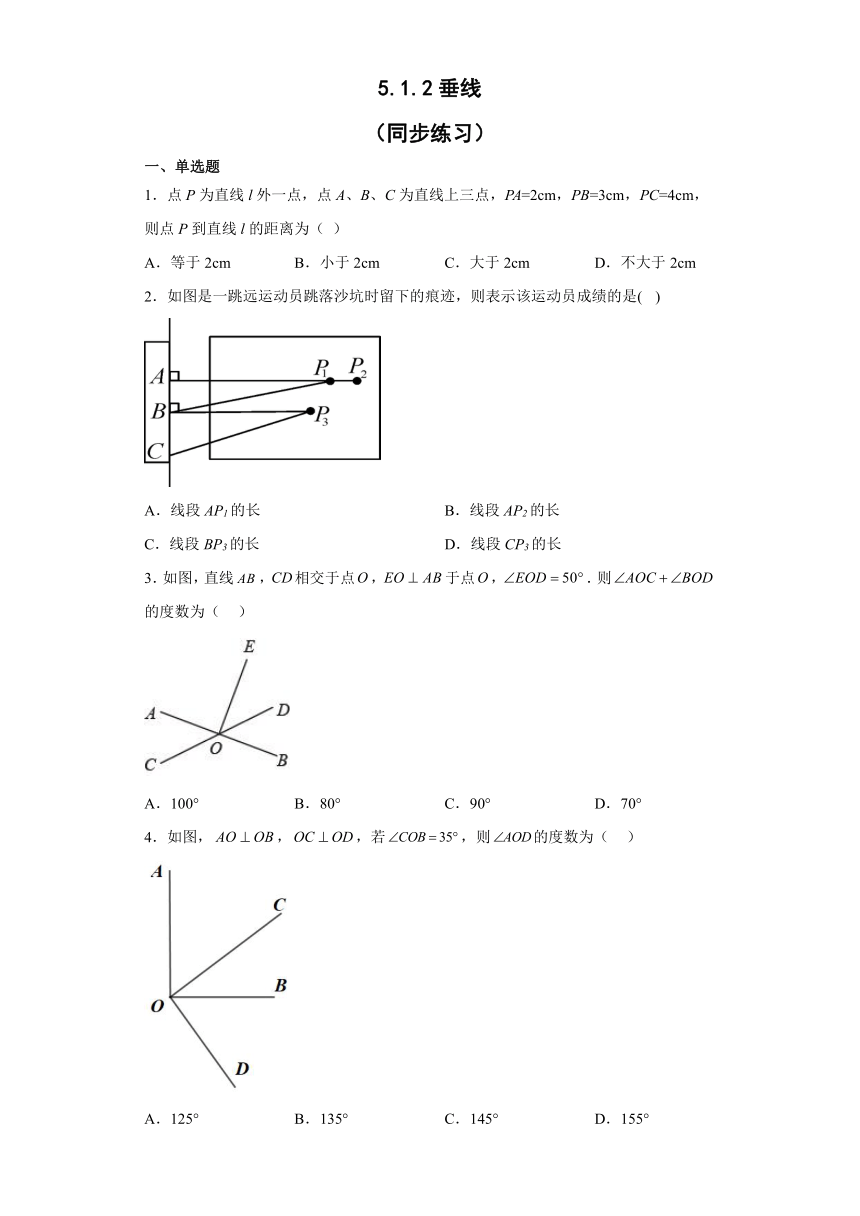
1.点P为直线l外一点,点A、B、C为直线上三点,PA=2cm,PB=3cm,PC=4cm,则点P到直线l的距离为( )
A.等于2cm B.小于2cm C.大于2cm D.不大于2cm
2.如图是一跳远运动员跳落沙坑时留下的痕迹,则表示该运动员成绩的是( )
A.线段AP1的长 B.线段AP2的长
C.线段BP3的长 D.线段CP3的长
3.如图,直线,相交于点,于点,.则的度数为( )
A.100° B.80° C.90° D.70°
4.如图,,,若,则的度数为( )
A.125° B.135° C.145° D.155°
5.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
6.点A为直线l外一点,点B在直线l上,若AB=5厘米,则点A到直线l的距离为
A.就是5厘米 B.大于5厘米
C.小于5厘米 D.最多为5厘米
7.平面内三条直线的交点个数可能有( )
A.个或个
B.个或个
C.个或个或个
D.个或个或个或个
8.如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的几何学原理是( )
A.垂线段最短
B.两点之间线段最短
C.两点确定一条直线
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
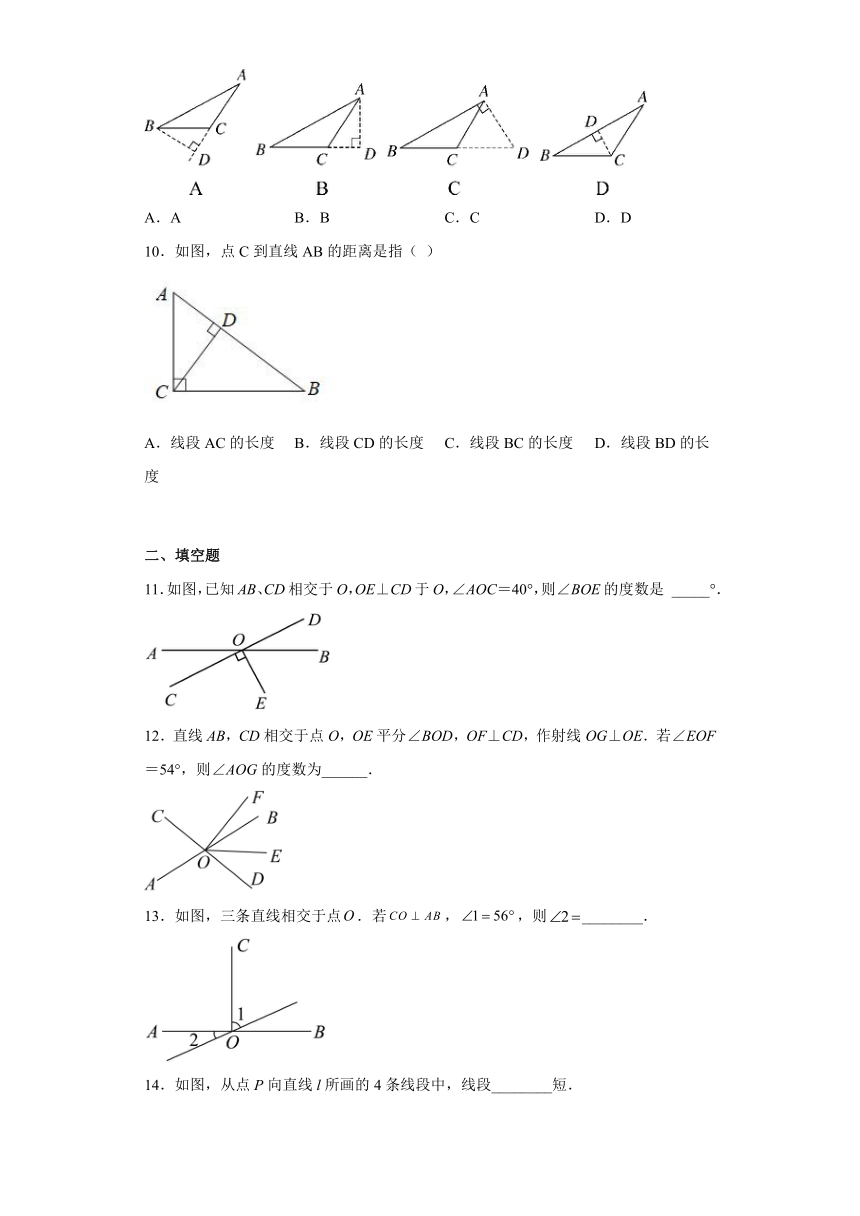
9.下列作图能表示点A到BC的距离的是( )
A.A B.B C.C D.D
10.如图,点C到直线AB的距离是指( )
A.线段AC的长度 B.线段CD的长度 C.线段BC的长度 D.线段BD的长度
二、填空题
11.如图,已知AB、CD相交于O,OE⊥CD于O,∠AOC=40°,则∠BOE的度数是 _____°.
12.直线AB,CD相交于点O,OE平分∠BOD,OF⊥CD,作射线OG⊥OE.若∠EOF=54°,则∠AOG的度数为______.
13.如图,三条直线相交于点.若,,则________.
14.如图,从点P向直线l所画的4条线段中,线段________短.
15.在体育课上某同学立定跳远的情况如图所示,直线l表示起跳线在测量该同学的实际立定跳远成绩时,应测量图中线段__________的长,理由是_______________.
三、解答题
16.阅读下面材料:小钟遇到这样一个问题:如图1,,请画一个,使与互补.
小钟是这样思考的:首先通过分析明确射线在的外部,画出示意图,如图2所示;然后通过构造平角找到的补角,如图3所示;进而分析要使与互补,则需;
因此,小钟找到了解决问题的方法:反向延长射线得到射线,利用量角器画出的平分线,这样就得到了与互补.
(1)请参考小钟的画法;在图4中画出一个,使与互余.并简要介绍你的作法;
(2)已知和互余,射线在的内部,且比大,请用表示的度数.
17.如图,的方向是北偏东,的方向是西偏北.
(1)若,则的方向是________;
(2)是的反向延长线,的方向是________;
(3)可看作是绕点顺时针方向旋转度至所形成的角,作的平分线,方向是________;
(4)在(1)、(2)、(3)的条件下,是的反向延长线,求的度数.
18.如图,点为直线上一点,为一射线,平分,平分.
(1)若,试探究,的位置关系,并说明理由.
(2)若为任意角,()中,的位置关系是否仍成立?请说明理由,由此你发现了什么规律?(数学思想链接:从特殊到一般)
19.如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄.
(1)设汽车行驶到公路AB上点P位置时,距离村庄M最近;行驶到点Q位置时,距离村庄N最近.请在图中的公路AB上分别画出点P,Q的位置(保留画图痕迹).
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离M,N两村庄都越来越近?在哪一段路上距离村庄N越来越近,而离村庄M却越来越远?(分别用文字表述你的结论,不必证明).
(3)到在公路AB上是否存在这样一点H,使汽车行驶到该点时,与村庄M,N的距离相等?如果存在,请在图中的AB上画出这一点(保留画图痕迹,不必证明);如果不存在,请简要说明理由.
20.如图,已知、、、是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
(1)画线段;
(2)画直线;
(3)过点画的垂线,垂足为;
(4)在直线上找一点,使得最小.
21.直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求:∠AOG的度数.
参考答案:
1.D2.B3.B4.C5.C6.D7.D8.A9.B10.B
11.50
12.54°或126°
13.34°
14.PB
15. PC 直线外一点与直线上各点连接的所有线段中,垂线段最短
16.(1)解:与互余,
,
,
射线在的外部,
先作(或)的垂线,再利用量角器画出(或)的平分线,如图所示:
或
(2)解:由题意,分以下两种情况:
①如图,当射线在的外部时,
和互余,
,
比大,
,即,
,
射线在的内部,,
;
②如图,当射线在的内部时,
射线在的内部,,
,
和互余,
,
,
比大,
,
,即,
,
解得,
综上,的度数为或.
17.(1)北偏东70°;
(2)南偏东40°;
(3)北偏东50°.
(4)
18.(1)解:.理由如下:
因为,
所以.
因为平分,平分,
所以,,
所以,
所以.
(2)解:成立.理由:
因为,
所以.
因为平分,平分,
所以,,
所以,
所以.
规律:邻补角的两条角平分线互相垂直.
19.(1)(3)如图,存在,
(2)在公路AB的AP上距离M,N两村庄都越来越近,在PQ路上距离村庄N越来越近,而离村庄M却越来越远.
20.解:如图
21.
(同步练习)
一、单选题
1.点P为直线l外一点,点A、B、C为直线上三点,PA=2cm,PB=3cm,PC=4cm,则点P到直线l的距离为( )
A.等于2cm B.小于2cm C.大于2cm D.不大于2cm
2.如图是一跳远运动员跳落沙坑时留下的痕迹,则表示该运动员成绩的是( )
A.线段AP1的长 B.线段AP2的长
C.线段BP3的长 D.线段CP3的长
3.如图,直线,相交于点,于点,.则的度数为( )
A.100° B.80° C.90° D.70°
4.如图,,,若,则的度数为( )
A.125° B.135° C.145° D.155°
5.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
6.点A为直线l外一点,点B在直线l上,若AB=5厘米,则点A到直线l的距离为
A.就是5厘米 B.大于5厘米
C.小于5厘米 D.最多为5厘米
7.平面内三条直线的交点个数可能有( )
A.个或个
B.个或个
C.个或个或个
D.个或个或个或个
8.如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的几何学原理是( )
A.垂线段最短
B.两点之间线段最短
C.两点确定一条直线
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
9.下列作图能表示点A到BC的距离的是( )
A.A B.B C.C D.D
10.如图,点C到直线AB的距离是指( )
A.线段AC的长度 B.线段CD的长度 C.线段BC的长度 D.线段BD的长度
二、填空题
11.如图,已知AB、CD相交于O,OE⊥CD于O,∠AOC=40°,则∠BOE的度数是 _____°.
12.直线AB,CD相交于点O,OE平分∠BOD,OF⊥CD,作射线OG⊥OE.若∠EOF=54°,则∠AOG的度数为______.
13.如图,三条直线相交于点.若,,则________.
14.如图,从点P向直线l所画的4条线段中,线段________短.
15.在体育课上某同学立定跳远的情况如图所示,直线l表示起跳线在测量该同学的实际立定跳远成绩时,应测量图中线段__________的长,理由是_______________.
三、解答题
16.阅读下面材料:小钟遇到这样一个问题:如图1,,请画一个,使与互补.
小钟是这样思考的:首先通过分析明确射线在的外部,画出示意图,如图2所示;然后通过构造平角找到的补角,如图3所示;进而分析要使与互补,则需;
因此,小钟找到了解决问题的方法:反向延长射线得到射线,利用量角器画出的平分线,这样就得到了与互补.
(1)请参考小钟的画法;在图4中画出一个,使与互余.并简要介绍你的作法;
(2)已知和互余,射线在的内部,且比大,请用表示的度数.
17.如图,的方向是北偏东,的方向是西偏北.
(1)若,则的方向是________;
(2)是的反向延长线,的方向是________;
(3)可看作是绕点顺时针方向旋转度至所形成的角,作的平分线,方向是________;
(4)在(1)、(2)、(3)的条件下,是的反向延长线,求的度数.
18.如图,点为直线上一点,为一射线,平分,平分.
(1)若,试探究,的位置关系,并说明理由.
(2)若为任意角,()中,的位置关系是否仍成立?请说明理由,由此你发现了什么规律?(数学思想链接:从特殊到一般)
19.如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄.
(1)设汽车行驶到公路AB上点P位置时,距离村庄M最近;行驶到点Q位置时,距离村庄N最近.请在图中的公路AB上分别画出点P,Q的位置(保留画图痕迹).
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离M,N两村庄都越来越近?在哪一段路上距离村庄N越来越近,而离村庄M却越来越远?(分别用文字表述你的结论,不必证明).
(3)到在公路AB上是否存在这样一点H,使汽车行驶到该点时,与村庄M,N的距离相等?如果存在,请在图中的AB上画出这一点(保留画图痕迹,不必证明);如果不存在,请简要说明理由.
20.如图,已知、、、是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
(1)画线段;
(2)画直线;
(3)过点画的垂线,垂足为;
(4)在直线上找一点,使得最小.
21.直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求:∠AOG的度数.
参考答案:
1.D2.B3.B4.C5.C6.D7.D8.A9.B10.B
11.50
12.54°或126°
13.34°
14.PB
15. PC 直线外一点与直线上各点连接的所有线段中,垂线段最短
16.(1)解:与互余,
,
,
射线在的外部,
先作(或)的垂线,再利用量角器画出(或)的平分线,如图所示:
或
(2)解:由题意,分以下两种情况:
①如图,当射线在的外部时,
和互余,
,
比大,
,即,
,
射线在的内部,,
;
②如图,当射线在的内部时,
射线在的内部,,
,
和互余,
,
,
比大,
,
,即,
,
解得,
综上,的度数为或.
17.(1)北偏东70°;
(2)南偏东40°;
(3)北偏东50°.
(4)
18.(1)解:.理由如下:
因为,
所以.
因为平分,平分,
所以,,
所以,
所以.
(2)解:成立.理由:
因为,
所以.
因为平分,平分,
所以,,
所以,
所以.
规律:邻补角的两条角平分线互相垂直.
19.(1)(3)如图,存在,
(2)在公路AB的AP上距离M,N两村庄都越来越近,在PQ路上距离村庄N越来越近,而离村庄M却越来越远.
20.解:如图
21.
